0.4 Repeated As A Fraction
salachar
Sep 11, 2025 · 5 min read
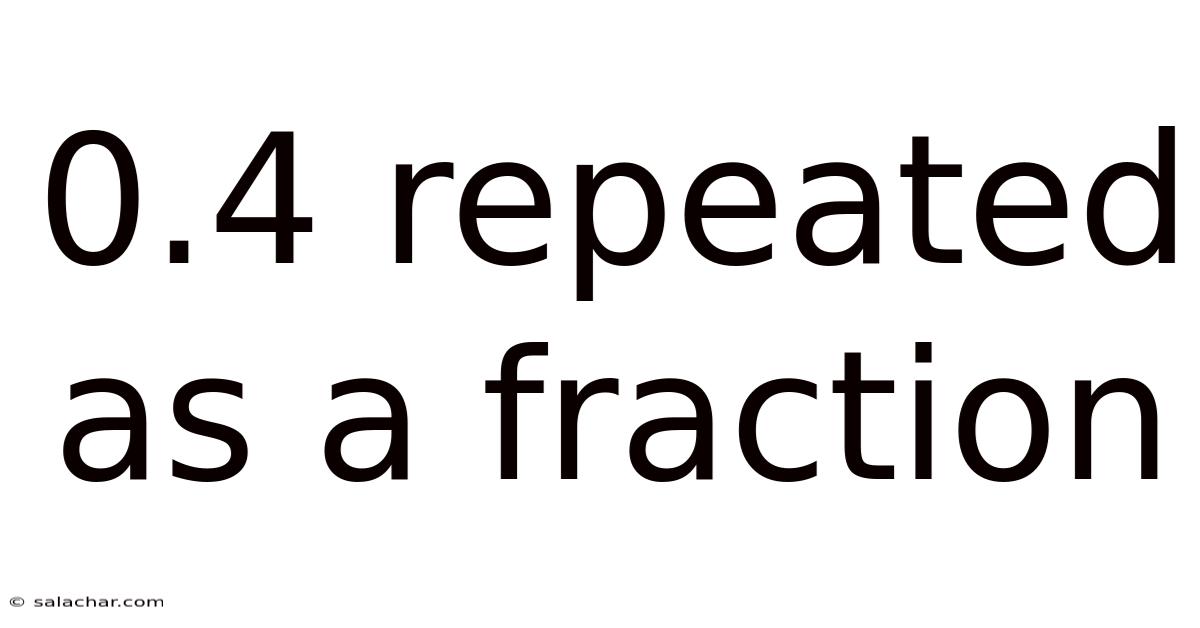
Table of Contents
Unveiling the Mystery: 0.4 Recurring as a Fraction
The seemingly simple decimal 0.4 recurring (often written as 0.444... or 0.<u>4</u>) can be a source of confusion for many. Understanding how to convert this repeating decimal into a fraction is a fundamental concept in mathematics, bridging the gap between decimal and fractional representations of numbers. This article will guide you through the process, explaining the underlying principles, providing step-by-step instructions, and exploring the broader mathematical context. We'll also delve into some common misconceptions and frequently asked questions.
Understanding Repeating Decimals
Before we dive into the conversion process, let's clarify what a repeating decimal is. A repeating decimal, or recurring decimal, is a decimal number where one or more digits repeat infinitely. In our case, the digit "4" repeats endlessly. This contrasts with terminating decimals, which have a finite number of digits after the decimal point, such as 0.25 or 0.75. Understanding this distinction is crucial for choosing the appropriate conversion method.
Method 1: The Algebraic Approach - A Classic Solution
This method is elegant and provides a solid understanding of the mathematical principles involved. It utilizes the properties of equations and algebraic manipulation to solve for the fractional representation.
Steps:
-
Let x equal the repeating decimal: We begin by assigning a variable, typically 'x', to represent the repeating decimal:
x = 0.444... -
Multiply by a power of 10: We multiply both sides of the equation by a power of 10 that shifts the repeating digits to the left of the decimal point. Since only one digit repeats, we multiply by 10:
10x = 4.444... -
Subtract the original equation: Subtracting the original equation (
x = 0.444...) from the equation obtained in step 2 (10x = 4.444...) eliminates the repeating part:10x - x = 4.444... - 0.444...9x = 4 -
Solve for x: Now, we solve for 'x' by dividing both sides by 9:
x = 4/9
Therefore, the fraction equivalent of 0.4 recurring is 4/9.
Method 2: The Geometric Series Approach - A More Advanced Perspective
This method leverages the concept of geometric series, a powerful tool in mathematics used to represent infinitely repeating sums. While more advanced, it offers a deeper understanding of the underlying mathematical structure.
A geometric series is a series where each term is obtained by multiplying the previous term by a constant value (called the common ratio). The formula for the sum of an infinite geometric series is:
S = a / (1 - r)
where:
Sis the sum of the infinite seriesais the first termris the common ratio (|r| < 1 for the series to converge)
In the case of 0.444..., we can represent it as a geometric series:
0.4 + 0.04 + 0.004 + 0.0004 + ...
Here:
a = 0.4(the first term)r = 0.1(the common ratio, each term is multiplied by 0.1 to get the next term)
Applying the formula:
S = 0.4 / (1 - 0.1) = 0.4 / 0.9 = 4/9
Again, we arrive at the fraction 4/9.
Why These Methods Work: A Deeper Dive
Both methods fundamentally rely on the concept of limits. A repeating decimal represents an infinite sum. The algebraic method cleverly manipulates this infinite sum to create a finite equation solvable for the fraction. The geometric series method directly represents the decimal as an infinite sum and uses a formula designed to calculate such sums. Both approaches, despite their different methods, lead to the same correct answer because they are based on sound mathematical principles dealing with infinite series and limits.
Common Misconceptions and Pitfalls
Several misconceptions surround converting repeating decimals to fractions. Let's address some of the most common ones:
-
Incorrect rounding: Simply rounding 0.444... to 0.4 or 0.44 is inaccurate. The repeating nature of the decimal implies an infinite number of 4s, which cannot be accurately represented by a finite decimal approximation.
-
Misunderstanding the concept of infinity: The key to successfully converting repeating decimals is understanding that the repetition continues indefinitely. This infinite repetition is what allows us to use algebraic manipulation or geometric series to find the equivalent fraction.
-
Assuming a pattern always implies a simple fraction: While many repeating decimals can be expressed as simple fractions, not all repeating decimals lead to easily identifiable fractions. The complexity of the fraction depends on the repeating pattern.
Expanding the Understanding: Repeating Decimals with Multiple Repeating Digits
The methods described above can be extended to handle repeating decimals with multiple repeating digits. For example, let's convert 0.121212... to a fraction:
x = 0.121212...100x = 12.121212...(Multiply by 100 because two digits repeat)100x - x = 12.121212... - 0.121212...99x = 12x = 12/99 = 4/33
Similarly, the geometric series approach can be adapted. The first term and common ratio will change depending on the repeating pattern.
Frequently Asked Questions (FAQ)
-
Q: Can all repeating decimals be expressed as fractions? A: Yes, all repeating decimals can be expressed as fractions. This is a fundamental property of the relationship between rational numbers (which can be expressed as fractions) and decimal representations.
-
Q: What if the repeating part doesn't start immediately after the decimal point? A: In such cases, you can first separate the non-repeating part and then apply the methods described above to the repeating part. For example, 0.2<u>5</u> can be handled by first subtracting 0.2, leaving 0.<u>05</u> which can be converted to a fraction as shown previously. Then add the 0.2 back as a fraction at the end.
-
Q: Are there any limitations to these methods? A: While these methods are effective for most repeating decimals, exceedingly long repeating patterns might require more complex algebraic manipulations or computational tools.
Conclusion: Mastering the Conversion
Converting a repeating decimal like 0.4 recurring into its fractional equivalent (4/9) is a cornerstone of mathematical understanding. This process demonstrates the interconnectedness between different numerical representations. By mastering the algebraic and geometric series methods, you'll not only be able to solve such problems efficiently but also gain a deeper appreciation for the underlying mathematical principles of infinite series and limits. Remember that the key is to understand the nature of repeating decimals and apply the appropriate method systematically. The process might seem challenging at first, but with practice, it becomes intuitive and rewarding. The ability to confidently navigate between decimal and fractional representations is a valuable skill applicable across numerous mathematical contexts.
Latest Posts
Latest Posts
-
Nouns That Begin With I
Sep 11, 2025
-
How Many Days Until 3 31 25
Sep 11, 2025
-
Where To Dispose Of Garbage
Sep 11, 2025
-
Is 10 Prime Or Composite
Sep 11, 2025
-
Guru Nanak Dev Ji Birth
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 0.4 Repeated As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.