1 2 4 8 16
salachar
Sep 03, 2025 · 6 min read
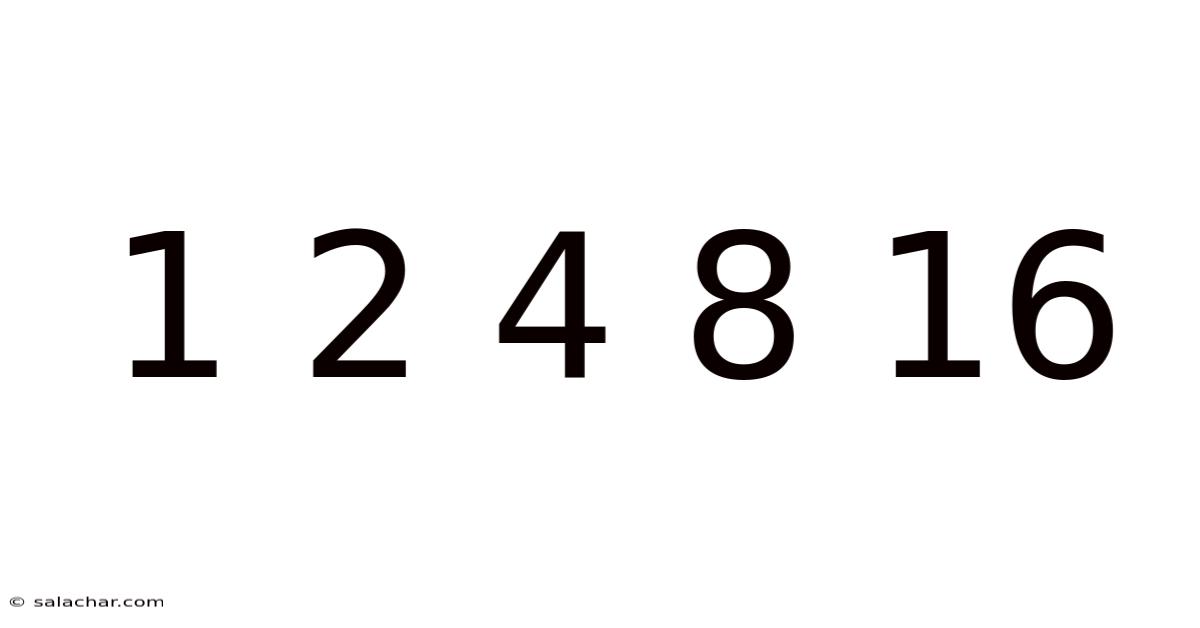
Table of Contents
Decoding the Power of 2: Exploring the Sequence 1, 2, 4, 8, 16, and Beyond
The seemingly simple sequence 1, 2, 4, 8, 16... might appear unremarkable at first glance. However, this deceptively straightforward progression holds immense significance across various fields, from basic arithmetic to advanced computer science and even the natural world. This sequence represents the fundamental concept of doubling, a core principle in exponential growth and a powerful tool for understanding patterns and relationships within seemingly disparate areas. This article delves deep into the fascinating world of this sequence, exploring its mathematical underpinnings, its practical applications, and its surprising connections to various aspects of life.
Understanding the Mathematical Basis: Exponential Growth and Powers of 2
The sequence 1, 2, 4, 8, 16 is a geometric progression. Each term is obtained by multiplying the preceding term by 2. This constant multiplicative factor is the key to understanding its exponential nature. Mathematically, this sequence can be expressed as 2<sup>0</sup>, 2<sup>1</sup>, 2<sup>2</sup>, 2<sup>3</sup>, 2<sup>4</sup>, and so on. This means each number in the sequence is a power of 2, where the exponent represents the position of the number in the sequence (starting from 0).
This exponential growth is characterized by increasingly rapid expansion. While the difference between consecutive terms initially seems small (1 to 2, 2 to 4), the gap widens dramatically as the sequence progresses. This rapid growth is a defining characteristic of exponential functions and is frequently encountered in various real-world scenarios.
Key mathematical concepts related to this sequence include:
- Exponential Functions: These functions describe processes where the rate of change is proportional to the current value. The sequence 1, 2, 4, 8, 16 is a prime example of an exponential function with a base of 2.
- Geometric Progression: This is a sequence where each term is obtained by multiplying the previous term by a constant value (in this case, 2).
- Powers of 2 (Binary System): The sequence directly relates to the binary numeral system, the foundation of modern computing. Binary uses only two digits (0 and 1) to represent numbers, and powers of 2 are crucial in understanding binary representation.
Practical Applications: From Computing to Biology
The sequence 1, 2, 4, 8, 16 and its extensions have far-reaching practical applications across numerous disciplines:
1. Computer Science and Digital Systems:
- Binary Numbers: The binary system, the bedrock of digital computing, relies heavily on powers of 2. Each bit (binary digit) represents a power of 2, enabling the representation of all numbers using only 0s and 1s. For example, the number 13 in decimal is represented as 1101 in binary (12³ + 12² + 02¹ + 12⁰ = 8 + 4 + 0 + 1 = 13).
- Memory Allocation: Computer memory is often organized in powers of 2 (kilobytes, megabytes, gigabytes, terabytes, etc.), directly reflecting the binary nature of computer systems.
- Data Structures and Algorithms: Many efficient algorithms and data structures, such as binary trees and binary search, leverage the properties of powers of 2 for optimized performance.
2. Biology and Natural World:
- Cell Division: The process of cell division often exhibits exponential growth, mirroring the doubling pattern of this sequence. A single cell dividing into two, then four, eight, and so on, demonstrates this principle.
- Population Growth (under ideal conditions): In ideal circumstances, certain populations (bacteria, for example) exhibit exponential growth, doubling their size within a fixed period.
- Branching Patterns: The branching patterns in trees and other biological structures sometimes approximate the doubling pattern, although this is not always a precise correspondence.
3. Music and Rhythm:
- Musical Scales and Intervals: While not a perfect match, certain musical scales and intervals have relationships that resonate with the doubling pattern. The octave, for example, represents a doubling of frequency.
4. Games and Puzzles:
- Chessboard Problem: The classic problem of placing grains of rice on a chessboard, doubling the amount on each successive square, demonstrates the rapid growth of exponential sequences.
Exploring Beyond 16: The Expanding Sequence and its Implications
While we've focused on the initial terms (1, 2, 4, 8, 16), the sequence continues indefinitely. As the numbers grow larger, the implications become even more profound:
- Large Numbers and Exponential Growth: The rapid escalation of the sequence highlights the power of exponential growth. The difference between 16 and 32 might seem modest compared to the vast difference between 2<sup>50</sup> and 2<sup>51</sup>. This demonstrates how small initial changes can lead to massive differences over time.
- Computational Limits: While computers can handle very large numbers, there are practical limits to the size of numbers they can represent and process efficiently. This becomes increasingly relevant as we consider extremely large powers of 2.
- Scientific Notation: For very large numbers in this sequence, scientific notation becomes essential for manageable representation.
Frequently Asked Questions (FAQ)
Q: What is the next number in the sequence 1, 2, 4, 8, 16?
A: The next number is 32 (16 x 2 = 32).
Q: Is this sequence related to Fibonacci numbers?
A: No, the sequence 1, 2, 4, 8, 16 is a geometric progression, while Fibonacci numbers are defined by a recursive relationship where each term is the sum of the two preceding terms (1, 1, 2, 3, 5, 8...). They are distinct mathematical concepts.
Q: Are there other sequences similar to this one?
A: Yes, any sequence where each term is obtained by multiplying the previous term by a constant factor is a geometric progression. The sequence 1, 3, 9, 27, 81... (powers of 3) is a similar example.
Q: What is the significance of the number 0 in the sequence?
A: Including 2⁰ = 1 maintains the consistent mathematical pattern of multiplying by 2. The exponent represents the position in the sequence, and starting at 2⁰ allows for a clear and consistent expression of the entire sequence.
Q: How is this sequence used in cryptography?
A: While not directly involved in the core algorithms, powers of 2 are fundamental to many aspects of computer security. They are integral to the underlying binary computations and data manipulation within cryptographic systems.
Conclusion: The Enduring Relevance of a Simple Sequence
The sequence 1, 2, 4, 8, 16, seemingly simple at first, reveals a depth of mathematical significance and widespread practical applications. From the fundamental building blocks of computer science to the processes of growth and division in the natural world, this sequence underscores the power of exponential growth and the pervasiveness of the number 2 in various aspects of life. Understanding this sequence provides valuable insights into diverse fields, highlighting the interconnectedness of mathematical concepts and their impact on our understanding of the world around us. Its seemingly simple nature belies its profound impact, showcasing the beauty and utility of mathematical patterns in a readily accessible and engaging way. The continued exploration of this sequence and its mathematical relatives promises to yield further understanding and innovation across numerous scientific and technological endeavors.
Latest Posts
Latest Posts
-
What Is A Rectilinear Motion
Sep 04, 2025
-
Imperial To Metric Conversion Table
Sep 04, 2025
-
Pictures Of Animals For Kids
Sep 04, 2025
-
Do Prokaryotes Have Golgi Apparatus
Sep 04, 2025
-
What Does The Stag Symbolize
Sep 04, 2025
Related Post
Thank you for visiting our website which covers about 1 2 4 8 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.