13 Percent In Decimal Form
salachar
Sep 12, 2025 · 5 min read
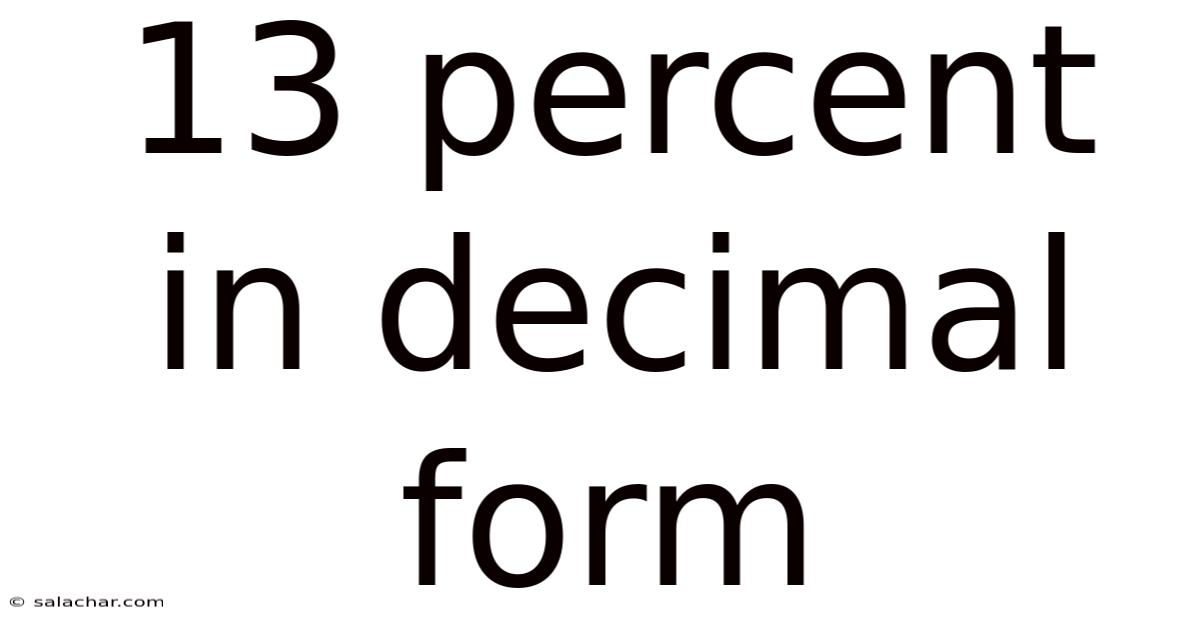
Table of Contents
13 Percent in Decimal Form: A Comprehensive Guide
Understanding percentages and their decimal equivalents is fundamental to various fields, from basic mathematics and finance to data analysis and scientific research. This comprehensive guide will delve into the conversion of 13 percent into its decimal form, explaining the underlying principles, providing practical examples, and exploring related concepts. We'll also address common misconceptions and frequently asked questions to ensure a thorough understanding of this crucial concept.
Introduction: Percentages and Decimals
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Decimals, on the other hand, are a way of representing numbers using the base-10 system, where each digit represents a power of 10. Converting between percentages and decimals is a straightforward process crucial for various calculations.
Converting 13 Percent to Decimal Form: The Simple Method
The most straightforward method for converting a percentage to a decimal is to divide the percentage by 100. In this case, we have 13 percent. Therefore, the calculation is:
13% ÷ 100 = 0.13
Therefore, 13 percent in decimal form is 0.13. This is the simplest and most widely used method.
Understanding the Process: A Deeper Dive
The conversion from percentage to decimal hinges on the definition of percentage itself. When we say 13%, we mean 13 out of 100, which can be written as the fraction 13/100. Dividing 13 by 100 gives us the decimal equivalent, 0.13. This is because the decimal point shifts two places to the left when dividing by 100. This is true for all percentage-to-decimal conversions.
Practical Applications of 13% in Decimal Form
The decimal form of 13%, 0.13, finds applications in numerous contexts:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins often requires converting percentages to decimals. For example, if a bank offers a 13% annual interest rate on a savings account, the decimal form (0.13) is used to calculate the interest earned each year.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions and probabilities. Converting them to decimals allows for easier calculations and comparisons. For instance, if 13% of a population possesses a certain characteristic, 0.13 represents the probability of randomly selecting an individual with that characteristic.
-
Scientific Research: In many scientific fields, data is expressed as percentages, which are subsequently converted to decimals for statistical analysis and modeling.
-
Everyday Calculations: Discounts in stores, calculating tips in restaurants, or determining the percentage of ingredients in a recipe all involve converting percentages to decimals for accurate calculations.
Further Exploration: Working with Other Percentages
The method for converting percentages to decimals remains consistent regardless of the percentage value. Let's consider a few examples:
- 25%: 25% ÷ 100 = 0.25
- 5%: 5% ÷ 100 = 0.05
- 150%: 150% ÷ 100 = 1.5 (Note that percentages greater than 100% result in decimals greater than 1)
- 0.5%: 0.5% ÷ 100 = 0.005
These examples demonstrate that the process is consistent and easily applicable across a range of percentages.
Converting Decimals Back to Percentages
The reverse process, converting decimals back to percentages, involves multiplying the decimal by 100 and adding the "%" symbol. For example:
- 0.13 × 100 = 13%
- 0.25 × 100 = 25%
- 1.5 × 100 = 150%
This demonstrates the reversible nature of the percentage-to-decimal conversion.
Common Misconceptions and Pitfalls
One common mistake is forgetting to divide by 100 when converting a percentage to a decimal. This leads to incorrect results. Always remember that a percentage represents a fraction of 100.
Another potential issue is misinterpreting decimals, especially those with leading zeros (e.g., 0.05). It's crucial to understand the place value of each digit in a decimal number.
Finally, be careful when working with percentages greater than 100%. Remember that these will result in decimals greater than 1.
Frequently Asked Questions (FAQ)
Q1: Can I convert 13% directly using a calculator?
A1: Yes, most calculators have a percentage function. You can simply enter "13%" and press the equals sign (=) to get the decimal equivalent (0.13). However, understanding the underlying process is still crucial.
Q2: Why is it important to know how to convert percentages to decimals?
A2: This skill is essential for various calculations involving proportions, ratios, probabilities, and financial applications. It's a fundamental building block for more advanced mathematical concepts.
Q3: What if I have a percentage with a decimal, like 13.5%?
A3: The conversion process remains the same: 13.5% ÷ 100 = 0.135. You simply divide the percentage by 100.
Q4: Are there any other ways to represent 13%?
A4: Yes, 13% can also be represented as the fraction 13/100. Both the decimal (0.13) and the fraction are equivalent representations of 13%.
Q5: What is the difference between a percentage and a ratio?
A5: A percentage is a specific type of ratio that expresses a quantity as a fraction of 100. A ratio is a more general comparison of two or more quantities. For example, 13:100 is a ratio equivalent to 13%.
Conclusion: Mastering Percentage-to-Decimal Conversions
Converting 13 percent to its decimal form, 0.13, is a simple yet crucial mathematical skill with widespread applications. Understanding the underlying principles and practicing the conversion process will enhance your ability to solve problems in various fields, from finance and statistics to everyday calculations. Remember the key: divide the percentage by 100 to get the decimal equivalent. This seemingly simple conversion is a foundation for more complex mathematical operations and a valuable tool in numerous practical situations. Mastering this skill will undoubtedly improve your numerical literacy and problem-solving abilities.
Latest Posts
Latest Posts
-
Can A Rectangle Be Rhombus
Sep 12, 2025
-
A Tisket A Tasket Meaning
Sep 12, 2025
-
Definition Of Memorandum Of Association
Sep 12, 2025
-
What The Factors Of 100
Sep 12, 2025
-
What Is A Draft Animal
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 13 Percent In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.