15 3 5 Of 250
salachar
Sep 13, 2025 · 5 min read
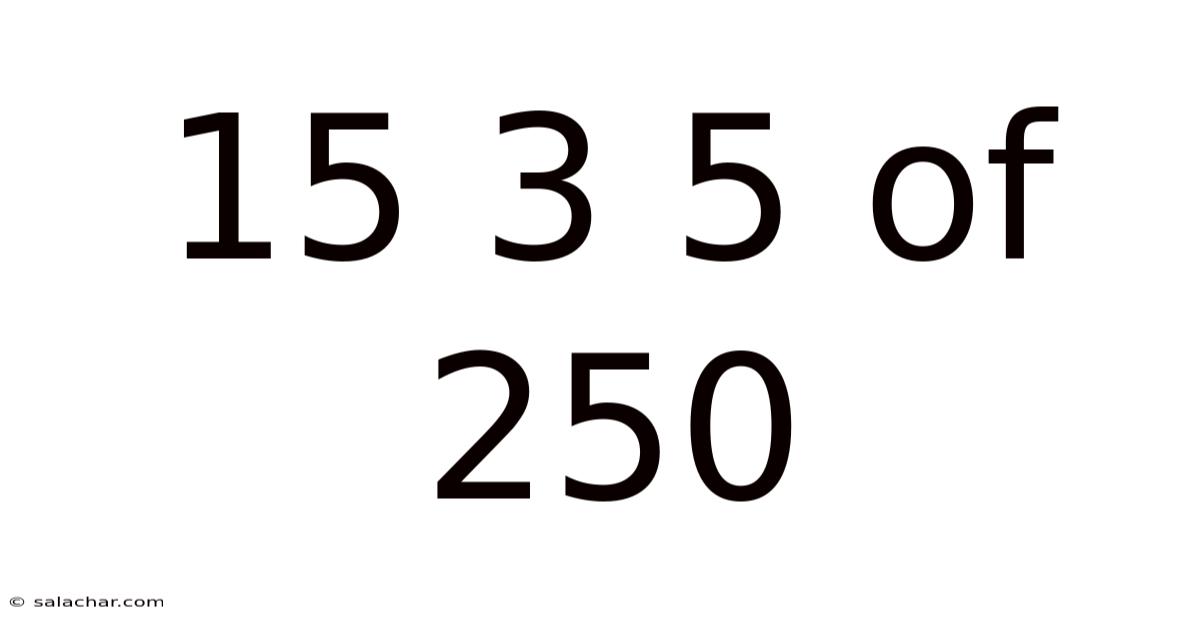
Table of Contents
Decoding the Enigma: Understanding the 15-3-5 of 250 in Statistical Analysis
The phrase "15-3-5 of 250" might sound like a cryptic code, but it actually represents a common scenario in statistical analysis, particularly within the context of sample size determination and statistical power. This article will delve into the meaning behind this seemingly simple phrase, exploring its implications for research design, and providing a comprehensive understanding of its application. We will break down the concept, clarifying its elements and highlighting its importance in ensuring the reliability and validity of research findings. This guide is intended for students, researchers, and anyone interested in learning more about the fundamentals of statistical analysis.
Understanding the Components: 15-3-5 of 250
Let's dissect the phrase "15-3-5 of 250." Each number represents a crucial element in a statistical power analysis:
-
250: This represents the total sample size of the study. It's the overall number of participants or observations included in the research.
-
15: This typically indicates the number of participants or observations within each group or condition. In a study comparing two groups (e.g., treatment vs. control), this would mean 15 participants in the treatment group and 15 in the control group.
-
3: This likely signifies the number of independent variables (IVs) or factors being investigated. These are the variables that the researcher manipulates or measures to observe their effects.
-
5: This often represents the number of dependent variables (DVs) or outcomes being measured. These are the variables that are expected to change as a result of manipulating the independent variables.
The Importance of Sample Size (n=250)
A sample size of 250 is considered relatively large in many research contexts. Larger samples generally lead to more precise estimations of population parameters and increased statistical power. Statistical power refers to the probability of finding a statistically significant effect if a true effect exists. A larger sample size reduces the chance of a Type II error (failing to reject a false null hypothesis—in simpler terms, missing a real effect). The choice of n=250 would depend on several factors including the effect size expected, the desired level of significance (alpha), and the desired power.
Multi-Variable Analysis: 3 Independent Variables and 5 Dependent Variables
The combination of 3 independent variables and 5 dependent variables suggests a complex research design, possibly involving analysis of variance (ANOVA), multiple regression analysis, or other multivariate techniques. Analyzing multiple variables simultaneously allows researchers to explore intricate relationships and interactions between factors. For instance, a study might examine the effects of three different teaching methods (IVs) on five different aspects of student learning (DVs), such as reading comprehension, writing skills, problem-solving abilities, critical thinking, and overall academic performance.
Implications for Statistical Power and Effect Size
The choice of 15 participants per group, along with the number of independent and dependent variables, directly influences the statistical power of the study. With a larger sample size (250), the study has a greater chance of detecting statistically significant effects, even if those effects are relatively small. However, the specific power will also depend on factors like the variability within each group and the chosen significance level (alpha). A power analysis should be conducted before the study begins to determine an appropriate sample size based on these factors, and this power analysis would likely justify the use of n=15 per group for the particular effect size and alpha level considered.
Practical Considerations and Limitations
While a sample size of 250 might seem substantial, its adequacy depends entirely on the context of the research. Factors like the population's variability, the desired level of precision, and the complexity of the analysis must be considered. In some fields, 250 may be considered small, while in others, it might be quite large. Moreover, simply having a large sample size doesn't automatically guarantee meaningful results. The quality of data collection, the validity of the measures used, and the appropriateness of the statistical analysis are equally crucial.
Frequently Asked Questions (FAQ)
Q: What does "15-3-5 of 250" mean in simpler terms?
A: It describes a research study involving 250 participants, divided into groups of 15. The study investigates how 3 different factors (independent variables) influence 5 different outcomes (dependent variables).
Q: Why is a sample size of 250 important?
A: A larger sample size (like 250) improves the precision of the results and increases the chances of detecting real effects (statistical power). It reduces the risk of Type II error (false negative).
Q: What kind of statistical analysis would be appropriate for this type of data?
A: Several multivariate statistical methods could be used, including ANOVA (Analysis of Variance), MANOVA (Multivariate Analysis of Variance), or multiple regression analysis, depending on the nature of the variables and research questions.
Q: How does the number of independent and dependent variables affect the analysis?
A: More variables increase the complexity of the analysis and require more sophisticated statistical techniques. It may also lead to challenges in interpretation, especially if there are interactions between the independent variables.
Q: What if the sample size wasn't 250? Would the interpretation change?
A: Yes, a smaller sample size would decrease statistical power, making it harder to detect significant effects. A larger sample size would increase power, but may not necessarily be more meaningful depending on the effect size and research context.
Conclusion: The Significance of Rigorous Research Design
The "15-3-5 of 250" represents a specific configuration within a broader framework of statistical research design. Understanding the components—sample size, number of groups, independent variables, and dependent variables—is crucial for interpreting research findings. While the specific numbers may vary depending on the research question and context, the principles remain constant: a well-designed study requires careful consideration of sample size, statistical power, and the appropriate statistical methods. A robust research design, including a thorough power analysis, is essential to ensure that the results are reliable, valid, and contribute meaningfully to the body of knowledge. Ignoring these considerations can lead to misleading or inconclusive results, hindering progress in various fields of study. The focus should always be on achieving a balance between feasible sample sizes and the necessary power to obtain meaningful and reliable findings.
Latest Posts
Latest Posts
-
The Bear William Faulkner Summary
Sep 13, 2025
-
Where To Buy Grain Alcohol
Sep 13, 2025
-
What Pumpkins Have Variegated Leaves
Sep 13, 2025
-
Where To Take My Trash
Sep 13, 2025
-
Can Humans Breathe On Mars
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 15 3 5 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.