2 2x X 2 0
salachar
Sep 12, 2025 · 5 min read
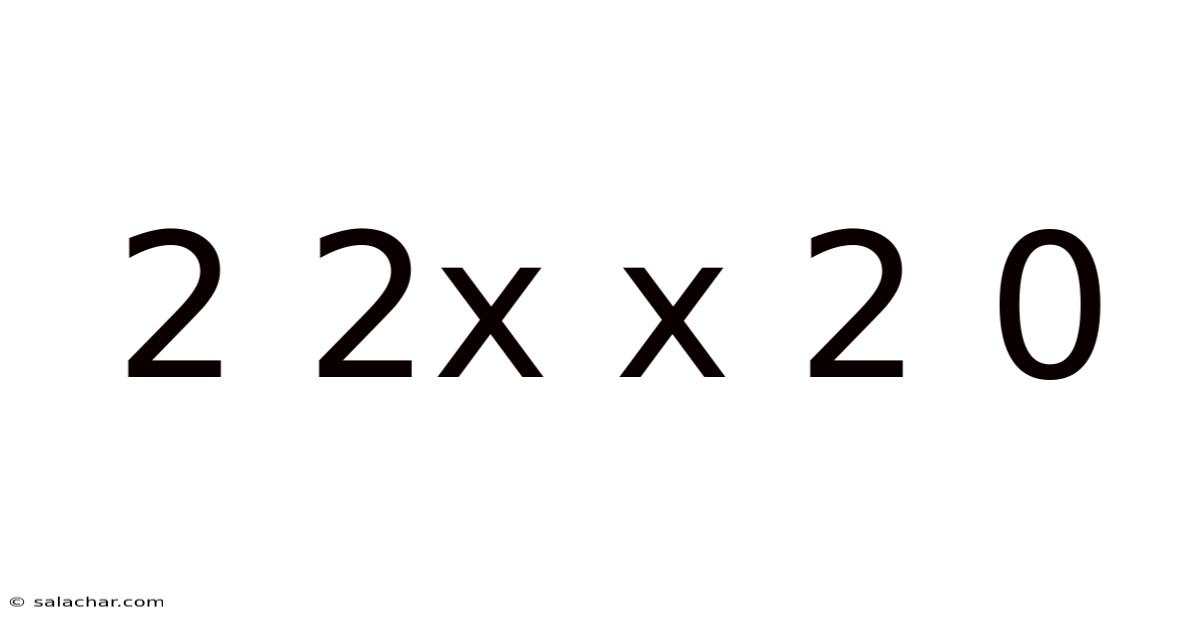
Table of Contents
Decoding the Enigma: A Deep Dive into the Expression "2 2x x 2 0"
The seemingly simple expression "2 2x x 2 0" presents a fascinating challenge. At first glance, it appears nonsensical, a jumble of numbers and symbols. However, a deeper exploration reveals potential interpretations depending on the context and intended meaning. This article will dissect this expression, exploring various mathematical and logical possibilities, addressing potential ambiguities, and ultimately providing a comprehensive understanding of its possible meanings. We'll delve into the importance of clear notation, the potential for hidden operations, and the significance of context in mathematical interpretation. This exploration will not only clarify the meaning of this specific expression but also serve as a valuable lesson in the precise communication essential in mathematics and beyond.
Understanding the Ambiguity: Why the Expression is Problematic
The primary issue with "2 2x x 2 0" lies in its lack of clear operational precedence. Standard mathematical notation uses symbols like +, -, ×, and ÷ to explicitly define the order of operations. The absence of these symbols leaves the expression open to multiple interpretations, each leading to a different numerical result. This ambiguity highlights the critical role of precise notation in mathematics. A slightly different arrangement or the addition of parentheses could drastically change the meaning and outcome.
For instance, the expression could be interpreted in several ways:
-
Scenario 1: Implicit Multiplication: One might interpret the expression as a series of implicit multiplications, leading to 2 * 2 * x * 2 * 0. In this case, the presence of 0 as a multiplier means the entire expression evaluates to 0, regardless of the value of x.
-
Scenario 2: Missing Operators: It is possible the spaces represent missing operators. The expression might be representing something like: 2 + 2x + x + 2 + 0, which simplifies to 4 + 3x.
-
Scenario 3: Typographical Error: It is also possible the expression is a typographical error. Perhaps an exponent was intended, a division sign was omitted, or a different arrangement of the numbers and variables was meant.
Exploring Possible Interpretations and Solutions
Let's systematically examine potential interpretations and their corresponding solutions:
1. Interpreting as Implicit Multiplication
If we assume implicit multiplication between all elements, the expression becomes:
2 × 2 × x × 2 × 0 = 0
In this interpretation, the result is unequivocally 0. The presence of 0 as a factor renders any other part of the expression irrelevant, as multiplication by zero always results in zero. This is a fundamental principle of arithmetic.
2. Introducing Parentheses: Altering the Order of Operations
Parentheses are crucial in mathematics for establishing the order of operations. By strategically placing parentheses, we can create different interpretations and obtain various outcomes. For example:
- (2 + 2x) × (2 + 0) = 2(2 + 2x) = 4 + 4x
This interpretation groups the first two elements and the last two, resulting in a linear expression.
- 2 + (2x × 2) + 0 = 2 + 4x
This interpretation demonstrates another way of adding parentheses, resulting in a different linear expression.
- (2 × 2x) × (2 × 0) = 0
Again, despite the parentheses, the multiplication by zero leads to the result of 0.
3. Considering Potential Typos: A Broader Perspective
The possibility of a typographical error cannot be disregarded. If the expression is part of a larger mathematical problem, context is essential for determining the intended meaning. Common errors include:
-
Missing Operators: The most likely error is the omission of operators. Did the author intend addition, subtraction, or division? The presence of an equal sign or an equation would provide valuable clues.
-
Misplaced Numbers or Variables: Did the author accidentally reverse the order of numbers or misplace the variable 'x'? For example, an intended equation might have been: 2x² + 2 = 0 which is a quadratic equation.
-
Exponential Notation: Perhaps the expression intended to include exponents. For instance, 2²x² x 2⁰ which simplifies to 4x². Note that 2⁰ = 1.
The Importance of Precise Mathematical Notation
The ambiguity surrounding "2 2x x 2 0" underscores the critical importance of precise mathematical notation. Ambiguous expressions can lead to confusion, misinterpretations, and incorrect results. Clear notation is essential for:
-
Unambiguous Communication: Precise notation ensures that mathematical expressions convey the intended meaning clearly and without ambiguity. This is particularly crucial in collaborative work or when communicating with others.
-
Accurate Calculations: Correctly formatted expressions facilitate accurate calculations and prevent errors arising from misinterpretations.
-
Efficient Problem-Solving: Clear notation simplifies problem-solving by reducing confusion and allowing for efficient application of mathematical rules and procedures.
The use of parentheses, proper spacing, and clear operator symbols are fundamental to preventing the issues highlighted by the expression "2 2x x 2 0".
Further Exploration and Advanced Concepts
While we've explored several basic interpretations, the expression's ambiguity opens doors to more advanced mathematical concepts:
-
Abstract Algebra: In abstract algebra, the expression might represent an operation within a particular algebraic structure, where the symbols have specialized meanings.
-
Functional Analysis: The 'x' could represent a variable in a function, and the expression might be part of a larger functional equation.
-
Symbolic Computation: Computer algebra systems could be used to manipulate and evaluate this expression based on assumptions about the intended meaning and the context of its use. This highlights the importance of specifying the rules of operations when using such systems.
Conclusion: Context is King
Ultimately, the meaning of "2 2x x 2 0" remains indeterminate without additional context. The expression's ambiguity showcases the necessity of precise mathematical notation and the critical role of context in interpretation. This exercise serves as a valuable reminder to always prioritize clear communication and to carefully check for errors or ambiguities before making calculations or presenting mathematical arguments. By acknowledging and addressing these issues, we can improve our understanding and application of mathematics, ensuring accuracy and clarity in all mathematical endeavors. The exploration of this seemingly simple expression has opened up a significant discussion about precision, clarity, and the importance of context in mathematical communication—fundamental skills for anyone working with numbers. Understanding the pitfalls of ambiguity allows for the development of more rigorous and reliable mathematical practices.
Latest Posts
Latest Posts
-
1 20 On The Periodic Table
Sep 12, 2025
-
How Is Paper Used Today
Sep 12, 2025
-
Units For Spring Constant K
Sep 12, 2025
-
Lab Equipment Names And Uses
Sep 12, 2025
-
Best Social Workers In Las Vegas
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 2 2x X 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.