3 Square Root Of 12
salachar
Sep 13, 2025 · 6 min read
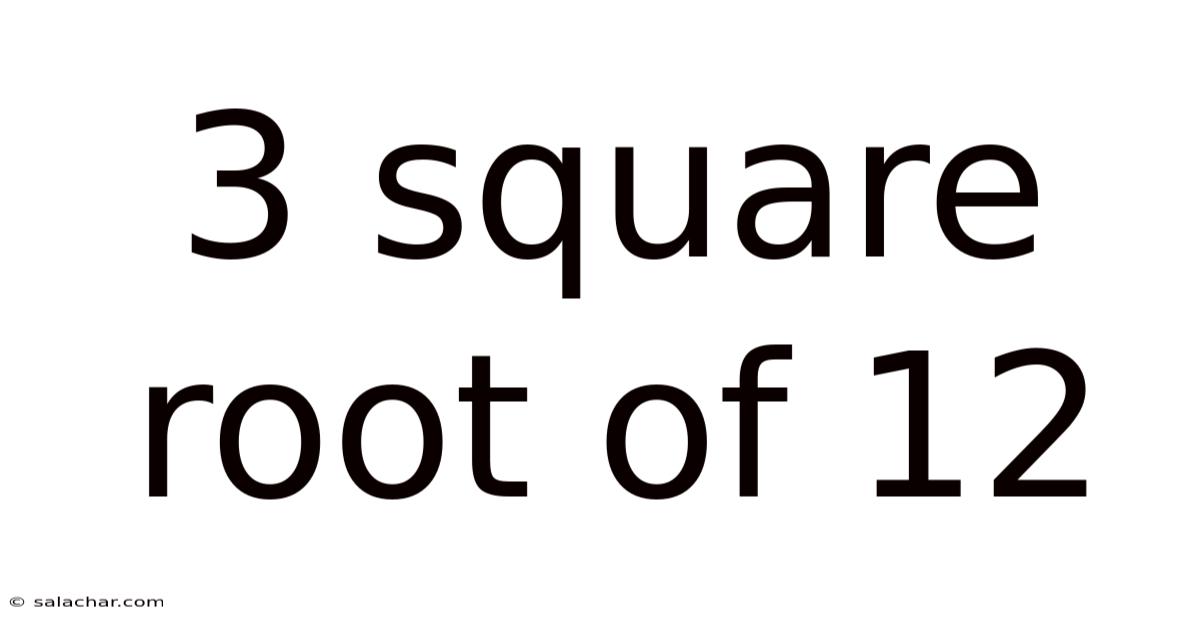
Table of Contents
Unveiling the Mystery: A Deep Dive into the Cube Root of 12
The cube root of 12, denoted as ³√12, might seem like a simple mathematical concept at first glance. However, a deeper exploration reveals a fascinating journey into the world of irrational numbers, approximation techniques, and the fundamental principles of algebra. This article aims to provide a comprehensive understanding of the cube root of 12, covering its calculation, applications, and broader mathematical significance. We'll explore various methods for finding its value, discuss its properties, and address frequently asked questions. By the end, you’ll possess a robust understanding of this seemingly simple yet surprisingly complex number.
Understanding Cube Roots
Before delving into the specifics of ³√12, let's establish a foundational understanding of cube roots. A cube root is a number that, when multiplied by itself three times (cubed), results in a given number. For instance, the cube root of 8 is 2 because 2 x 2 x 2 = 8. Cube roots, like square roots, are a fundamental concept in algebra and are used extensively in various fields, including geometry, physics, and engineering.
Unlike perfect cubes (numbers that have exact integer cube roots, like 8, 27, 64, etc.), the cube root of 12 is an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. This characteristic makes calculating its precise value a challenge, necessitating the use of approximation methods.
Methods for Approximating ³√12
Several methods can be employed to approximate the cube root of 12. Let's explore a few:
1. The Guess-and-Check Method: This is the most intuitive approach, especially for those unfamiliar with more advanced techniques. We start by guessing a number, cubing it, and then refining our guess based on whether the result is higher or lower than 12.
- Initial Guess: Let's start with 2. 2³ = 8, which is less than 12.
- Refined Guess: Let's try 2.5. 2.5³ = 15.625, which is greater than 12.
- Further Refinement: Since 2.5 is too high, we can try a value between 2 and 2.5, such as 2.2. 2.2³ ≈ 10.648, still too low. Continuing this process iteratively, we can progressively narrow down the approximation.
While this method is conceptually simple, it can be time-consuming and may not yield a highly precise result.
2. The Newton-Raphson Method: This is a powerful iterative numerical method for finding successively better approximations to the roots of a real-valued function. To apply it to find the cube root of 12, we need to consider the function f(x) = x³ - 12. The Newton-Raphson formula is:
x_(n+1) = x_n - f(x_n) / f'(x_n)
Where:
- x_n is the current approximation
- x_(n+1) is the next, improved approximation
- f(x_n) is the value of the function at x_n
- f'(x_n) is the derivative of the function at x_n (in this case, 3x_n²)
Starting with an initial guess (e.g., x_0 = 2), we repeatedly apply this formula until the difference between successive approximations becomes negligible. This method converges rapidly to the solution.
3. Using a Calculator or Computer Software: The most straightforward and efficient method is to use a scientific calculator or mathematical software (like MATLAB, Python with NumPy, etc.). These tools provide built-in functions to calculate cube roots directly, offering highly precise results. Using a calculator, we find that ³√12 ≈ 2.2894.
The Irrational Nature of ³√12 and its Decimal Representation
As mentioned earlier, ³√12 is an irrational number. Its decimal representation is non-terminating and non-repeating, meaning it goes on forever without exhibiting a repeating pattern. This is a fundamental property of many cube roots, especially those of non-perfect cubes. The decimal approximation we obtain using calculators or numerical methods is just an approximation, not the exact value. The more digits we include, the closer our approximation gets to the true value, but we can never reach the exact value because it is infinitely long.
Applications of Cube Roots
Cube roots, and more generally, roots of various orders, find diverse applications across various fields:
- Geometry: Calculating the side length of a cube given its volume involves finding the cube root. If the volume of a cube is 12 cubic units, then the length of its side is ³√12 units.
- Physics: Cube roots appear in various physics formulas, including those related to volume, density, and certain aspects of fluid dynamics.
- Engineering: In engineering design and calculations, cube roots are frequently used in structural analysis, fluid mechanics, and other areas.
- Finance: Cube roots are sometimes encountered in complex financial models and calculations related to compound interest and investment growth.
- Statistics: While less common than other mathematical functions, cube roots may appear in specific statistical calculations or data transformations.
Further Mathematical Explorations
The exploration of ³√12 can lead us to broader mathematical concepts:
- Nth Roots: The cube root is a specific case of the more general concept of nth roots. An nth root of a number x is a number y such that yⁿ = x.
- Complex Numbers: While we focused on real-valued cube roots, it's important to note that numbers have multiple cube roots when considering complex numbers (numbers involving the imaginary unit i, where i² = -1). The cube root of 12 has three cube roots in the complex plane.
- Series Expansions: Advanced mathematical techniques, such as Taylor series expansions, can be used to approximate the cube root of 12 (and other irrational numbers) with high accuracy.
Frequently Asked Questions (FAQ)
Q1: Is there a simple fraction that represents ³√12?
A1: No. ³√12 is an irrational number, meaning it cannot be expressed as a simple fraction (a ratio of two integers).
Q2: How accurate is the approximation ³√12 ≈ 2.2894?
A2: This is a reasonably accurate approximation, but it's still an approximation. The actual value has infinitely many digits after the decimal point. The accuracy depends on the context and the required precision.
Q3: Can I use a calculator to find the exact value of ³√12?
A3: Calculators and computer software can provide highly precise approximations, but not the exact value, as the true value is an irrational number with an infinite number of decimal places.
Q4: What are the other cube roots of 12 in the complex plane?
A4: While the real cube root of 12 is approximately 2.2894, there are two other complex cube roots. Finding these involves exploring complex numbers and their representation in the complex plane using polar coordinates and Euler's formula. This is a more advanced mathematical topic.
Q5: Are there any other methods to approximate the cube root of 12 besides the ones mentioned?
A5: Yes, there are other numerical methods, such as the bisection method and the secant method, which can be used to find approximations of cube roots. These methods have different convergence rates and computational requirements.
Conclusion
The cube root of 12, while seemingly simple, provides a rich opportunity to explore fundamental concepts in mathematics, from irrational numbers and approximation techniques to the broader field of numerical analysis and complex numbers. Understanding different methods of approximation and grasping the irrational nature of the result provides a deeper appreciation for the nuances of mathematics and its applications in diverse fields. This exploration highlights the beauty and complexity inherent in seemingly straightforward mathematical problems. By understanding the approaches and limitations involved in calculating the cube root of 12, we enhance our overall mathematical proficiency and problem-solving skills.
Latest Posts
Latest Posts
-
Is Solubility A Physical Property
Sep 13, 2025
-
Difference Between Amplitude And Frequency
Sep 13, 2025
-
How Tall Was A Brontosaurus
Sep 13, 2025
-
How To Draw A Chromosome
Sep 13, 2025
-
Days Until Feb 24 2025
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 Square Root Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.