3 Times What Equals 72
salachar
Sep 14, 2025 · 6 min read
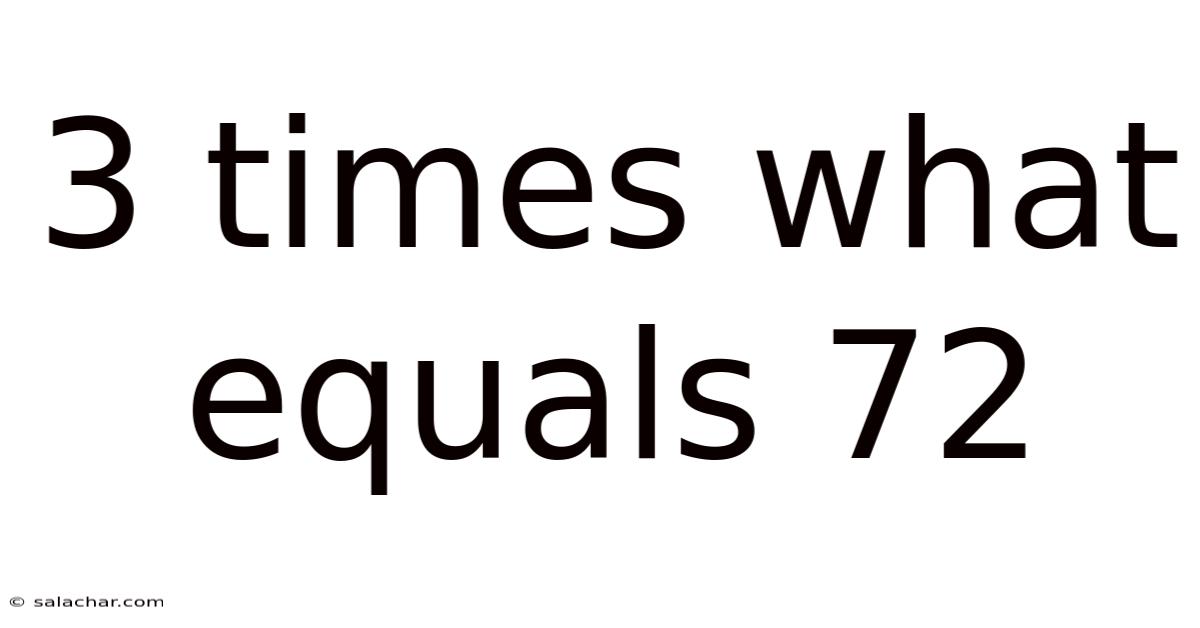
Table of Contents
Decoding the Mystery: 3 Times What Equals 72? A Deep Dive into Multiplication and Problem-Solving
Finding the answer to "3 times what equals 72?" might seem like a simple arithmetic problem, easily solved with a quick calculation. But this seemingly straightforward question opens a door to understanding fundamental mathematical concepts, problem-solving strategies, and even the beauty of mathematical relationships. This article will delve into not just the solution but also the broader implications of this simple equation, exploring different approaches, relatable examples, and even touching on the historical context of multiplication.
Understanding the Problem: Breaking Down "3 Times What Equals 72?"
At its core, the question "3 times what equals 72?" is a simple algebraic equation. We can represent it as:
3 * x = 72
Where 'x' is the unknown number we need to find. This equation asks: what number, when multiplied by 3, results in 72? Understanding this basic structure is crucial for tackling more complex mathematical problems in the future. This seemingly simple equation forms the foundation for understanding more complex algebraic concepts.
Method 1: Direct Division – The Most Efficient Approach
The most straightforward and efficient way to solve this problem is through division. Since multiplication and division are inverse operations, we can isolate 'x' by dividing both sides of the equation by 3:
3 * x / 3 = 72 / 3
This simplifies to:
x = 24
Therefore, 3 times 24 equals 72. This method is highly efficient and suitable for quick calculations.
Method 2: Repeated Subtraction – A Visual Approach to Understanding Multiplication
For those who find the abstract nature of division challenging, repeated subtraction provides a more intuitive approach. We can visualize this by repeatedly subtracting 3 from 72 until we reach zero:
72 - 3 = 69 69 - 3 = 66 66 - 3 = 63 ...and so on.
Counting how many times we subtract 3 will give us the answer. This method, while less efficient than division for larger numbers, offers a valuable visual representation of the relationship between multiplication and repeated subtraction. It reinforces the concept that multiplication is essentially repeated addition.
Method 3: Trial and Error – A Hands-on Approach to Problem Solving
Trial and error is a valuable problem-solving strategy, especially when dealing with smaller numbers. We can start by multiplying 3 by different numbers until we reach 72:
3 * 10 = 30 (Too low) 3 * 20 = 60 (Getting closer) 3 * 25 = 75 (Slightly too high) 3 * 24 = 72 (Correct!)
While this method might be less efficient for larger numbers, it highlights the iterative nature of problem-solving and emphasizes the importance of making educated guesses and adjusting based on the results.
Method 4: Using a Multiplication Table – A Quick Reference Tool
A multiplication table is a valuable tool for quickly finding the answer to multiplication problems. By locating the number 72 in the row corresponding to the multiplier 3 (or vice versa), we can directly identify the unknown number (24). This method relies on prior memorization of multiplication facts, a valuable skill for quicker calculations.
Expanding the Understanding: Real-World Applications and Contextualization
The simple equation "3 times what equals 72?" might seem isolated, but its applications are numerous and relevant to various aspects of daily life. Consider these examples:
- Dividing resources: Imagine you have 72 candies to distribute equally among 3 friends. The solution (24) tells you how many candies each friend will receive.
- Calculating unit cost: If 3 identical items cost $72, dividing the total cost by the number of items gives you the cost of a single item ($24).
- Scaling recipes: A recipe calls for 3 cups of flour, but you want to triple the recipe. Knowing that 3 times 24 equals 72, you'll need 72 cups of flour for the tripled recipe.
- Geometric problems: Consider a rectangle with an area of 72 square units and a width of 3 units. The solution (24) represents the length of the rectangle.
These examples illustrate the practical applications of understanding multiplication and division in everyday scenarios.
Delving Deeper: The Mathematical Foundation of Multiplication
Multiplication, at its core, represents repeated addition. When we say "3 times 24," we're essentially adding 24 three times: 24 + 24 + 24 = 72. Understanding this fundamental principle is crucial for grasping more advanced mathematical concepts.
Multiplication is also commutative, meaning the order of the numbers doesn't change the result. 3 * 24 is the same as 24 * 3. This property is often overlooked but crucial for simplifying calculations. It allows us to approach problems from different angles.
Furthermore, multiplication is associative, meaning that the grouping of numbers doesn't affect the product. For example, (3 * 2) * 12 = 3 * (2 * 12) = 72. This property is vital for performing more complex calculations efficiently. Understanding the associative and commutative properties expands the versatility of solving mathematical problems and enhances comprehension of more advanced algebraic concepts.
The Historical Context of Multiplication
Multiplication, as a concept, has been around for millennia. Ancient civilizations developed various methods for multiplication, including the use of tally marks, abacuses, and even specialized algorithms. Understanding the historical evolution of multiplication helps appreciate its significance in the development of mathematics and its ongoing relevance in our modern world. Different cultures developed unique methods for multiplication; however, the underlying principle of repeated addition remained consistent.
Frequently Asked Questions (FAQ)
-
What if the question was "What number multiplied by 3 gives 72?" The question is essentially the same; the solution remains 24.
-
Can this problem be solved using fractions? Yes, the equation can be written as (1/3) * 72 = x, which still results in x = 24.
-
Are there other ways to represent this problem? Yes, it can be expressed as 3x = 72, or even in word problems as described in the real-world applications section.
-
What happens if we change the number 3 or 72? Changing either number will yield a different solution. For example, if the problem was "5 times what equals 72?", the solution would be 72/5 = 14.4.
Conclusion: More Than Just a Simple Equation
The seemingly simple question, "3 times what equals 72?", unlocks a deeper understanding of mathematical principles, problem-solving strategies, and the practical applications of arithmetic in everyday life. From basic division to more nuanced methods like repeated subtraction and trial and error, multiple approaches exist to arrive at the solution (24). Understanding the underlying concepts, such as the commutative and associative properties of multiplication, further solidifies one's grasp of mathematical foundations. This simple equation, therefore, serves as a gateway to exploring the vast and fascinating world of mathematics. Remember that the ability to approach problems from multiple angles and develop a nuanced understanding of mathematical relationships is far more valuable than simply obtaining the correct answer.
Latest Posts
Latest Posts
-
What Is The Smallest Cell
Sep 14, 2025
-
Lewis Dot Structure For Arsenic
Sep 14, 2025
-
2 Mg L To Ppm
Sep 14, 2025
-
Guru Nanak Dev Ji Pictures
Sep 14, 2025
-
Air Is Heterogeneous Or Homogeneous
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 Times What Equals 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.