4 5 As A Percent
salachar
Sep 14, 2025 · 5 min read
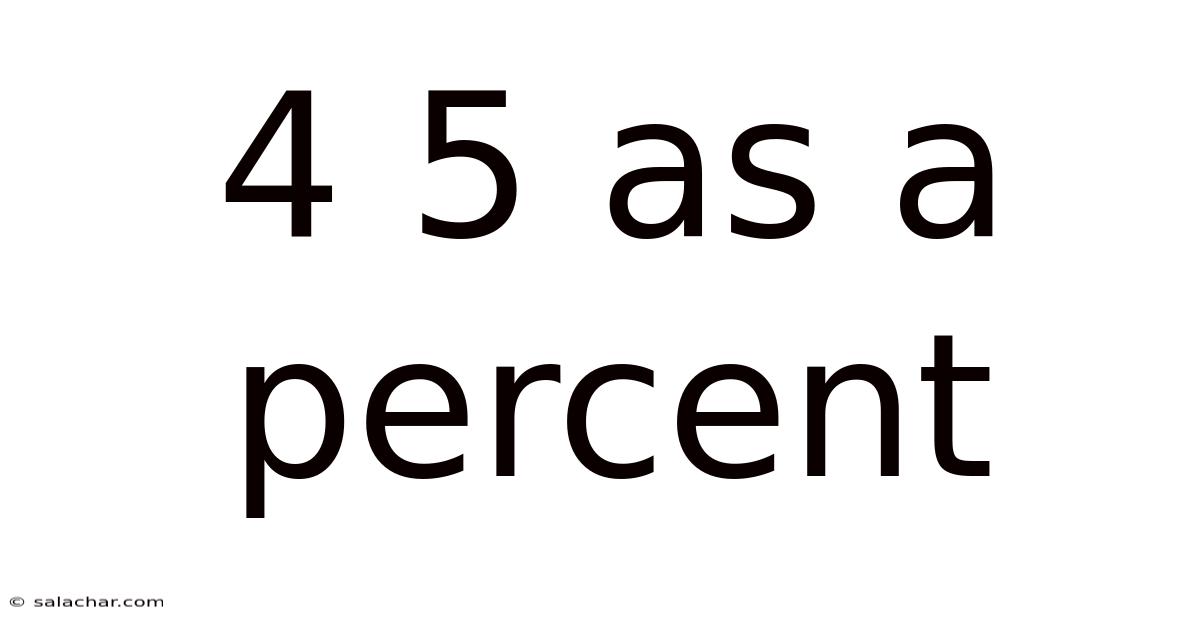
Table of Contents
Understanding 4/5 as a Percent: A Comprehensive Guide
What is 4/5 as a percent? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics crucial for everyday life and various academic disciplines. This comprehensive guide will not only answer the question directly but also explore the underlying principles, providing you with the tools to confidently convert any fraction to a percentage. We'll delve into the methods, explain the reasoning behind them, and address frequently asked questions to ensure a thorough grasp of this important mathematical skill.
Understanding Fractions, Decimals, and Percentages
Before diving into the specific conversion of 4/5, let's establish a solid foundation. These three concepts are interconnected, representing different ways to express parts of a whole:
-
Fractions: Express a part of a whole using a numerator (top number) and a denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts. For example, 4/5 means you have 4 out of 5 equal parts.
-
Decimals: Represent parts of a whole using the base-10 number system. The decimal point separates the whole number from the fractional part. For example, 0.8 represents eight-tenths.
-
Percentages: Express parts of a whole as a fraction of 100. The percentage symbol (%) signifies "out of 100." For example, 80% means 80 out of 100.
The key is that these representations are interchangeable. We can convert between them using specific mathematical operations.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is a two-step process:
Step 1: Convert the fraction to a decimal. To do this, divide the numerator (4) by the denominator (5):
4 ÷ 5 = 0.8
Step 2: Convert the decimal to a percentage. To convert a decimal to a percentage, multiply by 100 and add the percentage symbol (%):
0.8 × 100 = 80%
Therefore, 4/5 is equal to 80%.
Method 2: Direct Conversion using the Concept of "Out of 100"
A percentage is fundamentally a fraction with a denominator of 100. We can directly convert 4/5 to a percentage by finding an equivalent fraction with a denominator of 100:
We need to find a number that, when multiplied by 5, gives 100. That number is 20 (5 x 20 = 100). To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by 20:
(4 x 20) / (5 x 20) = 80/100
Since 80/100 means 80 out of 100, this directly translates to 80%.
Method 3: Using Proportions
This method employs the power of proportions to solve the problem. We can set up a proportion to find the percentage:
4/5 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
5x = 400
Now, divide both sides by 5:
x = 80
Therefore, 4/5 is equal to 80%.
Understanding the Relationship: Fractions, Decimals, and Percentages
Let's consolidate our understanding by looking at the interrelationship between these three representations for the specific example of 4/5:
-
Fraction: 4/5 represents four-fifths of a whole.
-
Decimal: 0.8 represents eight-tenths, which is equivalent to four-fifths. Notice that the decimal 0.8 is obtained by dividing 4 by 5.
-
Percentage: 80% represents eighty hundredths, which is also equivalent to four-fifths. This is obtained by multiplying the decimal 0.8 by 100.
This interconnectedness allows for flexibility in choosing the most convenient representation for a particular problem or situation.
Real-World Applications of Percentage Conversions
The ability to convert fractions to percentages is vital in numerous real-world scenarios:
-
Calculating Discounts: If a store offers a 20% discount on an item, understanding this as 1/5 (20/100 simplifies to 1/5) helps quickly calculate the discount amount.
-
Understanding Test Scores: A test score of 85% clearly indicates that you answered 85 out of 100 questions correctly. This can be expressed as a fraction (85/100, which simplifies to 17/20) for a better understanding of your performance.
-
Financial Calculations: Interest rates, taxes, and investment returns are often expressed as percentages, demanding a solid understanding of fraction-to-percentage conversions for accurate calculations.
-
Data Analysis: Representing data in percentages allows for easy comparison and interpretation of various proportions within a dataset.
Advanced Applications: Extending the Concept
The principles applied to converting 4/5 to a percentage can be extended to convert any fraction to a percentage. The core idea remains the same: find an equivalent fraction with a denominator of 100, or convert the fraction to a decimal and then to a percentage.
For example, let's convert 3/8 to a percentage:
-
Divide the numerator by the denominator: 3 ÷ 8 = 0.375
-
Multiply by 100 and add the percentage symbol: 0.375 × 100 = 37.5%
Frequently Asked Questions (FAQ)
Q1: What if the fraction is an improper fraction (numerator > denominator)?
A: The process remains the same. Convert the improper fraction to a mixed number (whole number and a proper fraction), convert the proper fraction part to a decimal, and then to a percentage. Add the whole number part to the resulting percentage. For example, 7/5 = 1 2/5. 2/5 = 0.4, which is 40%. Therefore, 7/5 is 140%.
Q2: Can I use a calculator for these conversions?
A: Absolutely! Calculators can simplify the division and multiplication steps, making the process quicker and reducing the risk of calculation errors.
Q3: What are some common percentage equivalents to know?
A: Knowing common fraction-percentage equivalents (e.g., 1/2 = 50%, 1/4 = 25%, 1/5 = 20%, 1/10 = 10%) can significantly speed up calculations and enhance your mental math skills.
Conclusion: Mastering Percentage Conversions
Converting 4/5 to a percentage – whether through direct conversion, using decimals, or employing proportions – reinforces the fundamental relationship between fractions, decimals, and percentages. Understanding these conversions is not just about solving a math problem; it's about acquiring a skill applicable in countless real-world situations, from managing finances to interpreting data. By mastering these methods, you enhance your mathematical literacy and build a stronger foundation for tackling more complex mathematical challenges. Remember to practice regularly, applying these concepts to various examples, to solidify your understanding and build confidence in your ability to seamlessly convert between fractions and percentages.
Latest Posts
Latest Posts
-
Does Black Panther Have Powers
Sep 14, 2025
-
How To Calculate Power Statistics
Sep 14, 2025
-
Iodine State At Room Temperature
Sep 14, 2025
-
How Many Minutes Till 2 30
Sep 14, 2025
-
Noise Intensity Is Measured In
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4 5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.