40 40 X 0 1
salachar
Sep 15, 2025 · 6 min read
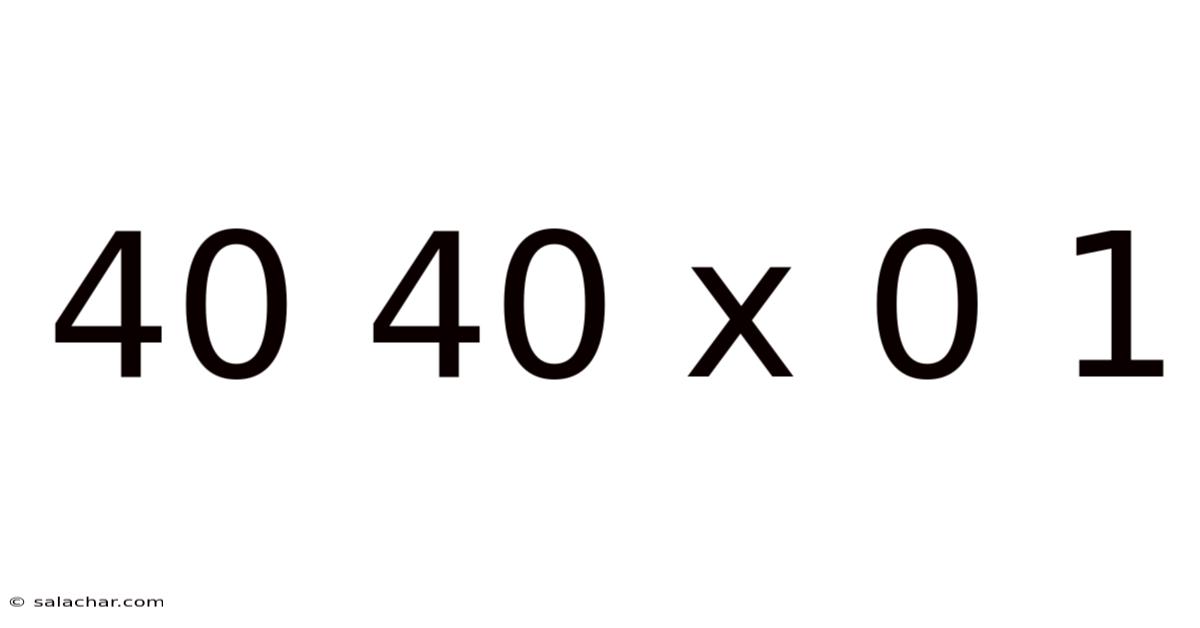
Table of Contents
Decoding 40x40x0.1: Exploring the World of Volume Calculations and Beyond
Understanding the calculation "40 x 40 x 0.1" might seem straightforward at first glance: a simple multiplication problem. However, this seemingly basic calculation opens doors to a wide range of applications, particularly in understanding volume, area, and the practical implications of these concepts in various fields. This article will delve into the mechanics of this calculation, explore its significance in different contexts, and unravel its implications beyond the purely mathematical. We will also examine the potential for misinterpretations and the importance of clear units of measurement.
Understanding the Basics: Volume Calculation
The expression "40 x 40 x 0.1" represents a volume calculation. Volume, in its simplest form, is the amount of three-dimensional space occupied by an object or substance. The calculation assumes a rectangular prism (or cuboid) – a three-dimensional shape with six rectangular faces.
The Formula: The volume of a rectangular prism is calculated by multiplying its length, width, and height. In our case:
- Length = 40 (units)
- Width = 40 (units)
- Height = 0.1 (units)
Therefore, Volume = 40 x 40 x 0.1 = 160 cubic units.
Crucial Note: The units are absolutely critical. Without specifying the units (e.g., centimeters, meters, inches, feet), the numerical value "160" is meaningless. If the units were centimeters, the volume would be 160 cubic centimeters (cm³). If the units were meters, the volume would be 160 cubic meters (m³), a significantly larger volume. Always clarify the units of measurement!
Applications Across Diverse Fields
The seemingly simple calculation of 40 x 40 x 0.1 has wide-ranging applications in various fields:
1. Construction and Engineering:
Imagine calculating the volume of concrete needed for a foundation. If the foundation measures 40 feet by 40 feet and requires a depth of 0.1 feet (or 1.2 inches), this calculation directly determines the volume of concrete needed. This translates directly into material costs and logistical planning. Similar calculations are vital in determining the volume of earth to be excavated for a basement or the volume of a water tank.
2. Agriculture and Horticulture:
In agriculture, this calculation could determine the volume of soil in a raised garden bed. Understanding the soil volume is crucial for calculating fertilizer requirements and assessing water retention capacity. Similarly, in horticulture, it could help determine the volume of potting mix needed for a large planter.
3. Manufacturing and Packaging:
Manufacturing processes often involve precise volume calculations. For example, this calculation could represent the internal volume of a container designed to hold a specific product. Accurate volume calculations are crucial for efficient packaging, preventing product damage, and ensuring accurate labeling.
4. Medicine and Pharmaceuticals:
Precise volume measurements are critical in pharmaceutical applications. This calculation could represent the volume of a particular solution or the capacity of a medical device. Accuracy in these contexts is paramount for patient safety and treatment efficacy.
Beyond Simple Volume: Exploring Related Concepts
The 40 x 40 x 0.1 calculation extends beyond simple volume calculations. Let's explore some related concepts:
1. Surface Area: While we focused on volume, understanding the surface area of the rectangular prism is equally important in various applications. The surface area influences factors like heat transfer, material costs, and the amount of paint needed to coat a surface. The surface area calculation for a rectangular prism involves calculating the area of each face and summing them up. This adds another layer of complexity to the problem and highlights the interdependency of geometric concepts.
2. Scaling and Proportionality: Imagine scaling up or down the dimensions. If we double the length and width to 80 x 80, keeping the height at 0.1, the volume increases significantly. This exemplifies the concept of proportionality and how changes in dimensions directly impact the volume. Understanding this principle is crucial in designing and scaling models or structures.
3. Unit Conversions: Mastering unit conversions is essential when dealing with volume calculations. Converting cubic centimeters to liters, cubic feet to cubic yards, or other units is a common task. This involves understanding the relationships between different units and applying appropriate conversion factors.
4. Error Analysis: In real-world applications, measurements are rarely perfectly precise. Considering potential errors in measurements is crucial for accurate volume estimations. Understanding error propagation and how measurement uncertainties affect the final volume calculation is critical for reliable results.
Potential Misinterpretations and Avoiding Mistakes
Several potential pitfalls can lead to incorrect interpretations of the 40 x 40 x 0.1 calculation:
-
Ignoring Units: As emphasized before, neglecting units is the most common mistake. Always specify the units of measurement to avoid ambiguity and ensure accurate results.
-
Incorrect Interpretation of Dimensions: Ensure that the dimensions (40, 40, and 0.1) represent the correct length, width, and height of the object. Misinterpreting these dimensions will lead to an incorrect volume calculation.
-
Assuming a Regular Shape: The calculation applies specifically to a rectangular prism. If the object is irregular in shape, more complex methods (e.g., integration or water displacement) are required to determine its volume.
-
Rounding Errors: Rounding off numbers during intermediate steps can accumulate errors, leading to significant discrepancies in the final result. It's advisable to use the full precision of the numbers throughout the calculation.
Frequently Asked Questions (FAQ)
Q: What if the dimensions are not perfectly rectangular?
A: If the shape deviates from a perfect rectangular prism, the simple 40 x 40 x 0.1 formula is no longer applicable. More advanced techniques, such as dividing the object into smaller rectangular prisms or using integration, would be necessary.
Q: How do I convert cubic units to other units (e.g., liters, gallons)?
A: Conversion factors are needed to change units. For instance, to convert cubic centimeters to liters, you would use the conversion factor 1000 cm³ = 1 liter. Similar conversion factors exist for other units. Consulting a conversion table or using online conversion tools can be helpful.
Q: What is the significance of the decimal value (0.1) in the calculation?
A: The decimal value represents the height of the rectangular prism. Its small value suggests a relatively thin or shallow object compared to its length and width. This can be relevant in various contexts, like thin layers of material or shallow foundations.
Q: Can this calculation be applied to irregular shapes?
A: No, this calculation is specifically for rectangular prisms. For irregular shapes, you would need to use different methods (e.g., water displacement, integration techniques) to determine the volume accurately.
Q: What if I want to find the volume of a cylinder instead of a rectangular prism?
A: The formula for the volume of a cylinder is different. The formula is V = πr²h, where 'r' is the radius and 'h' is the height. The calculation 40 x 40 x 0.1 would not be applicable.
Conclusion: The Power of a Simple Calculation
The seemingly simple calculation 40 x 40 x 0.1 underscores the fundamental importance of geometric principles and their widespread applications. While the calculation itself is straightforward, understanding its context, potential applications, and associated concepts is crucial for solving real-world problems across numerous fields. Remember to always pay attention to units of measurement, consider potential sources of error, and select the appropriate formula based on the object's shape to ensure accurate and reliable results. The seemingly basic math behind this calculation holds significant practical power, extending beyond the classroom into the intricate workings of many industries.
Latest Posts
Latest Posts
-
Weather In India In July
Sep 15, 2025
-
Life In A Large City
Sep 15, 2025
-
Partial Product In Math Definition
Sep 15, 2025
-
Welcome Address For An Event
Sep 15, 2025
-
Dibujo Armas De Los Espanoles
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 40 40 X 0 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.