44 50 As A Percent
salachar
Sep 07, 2025 · 5 min read
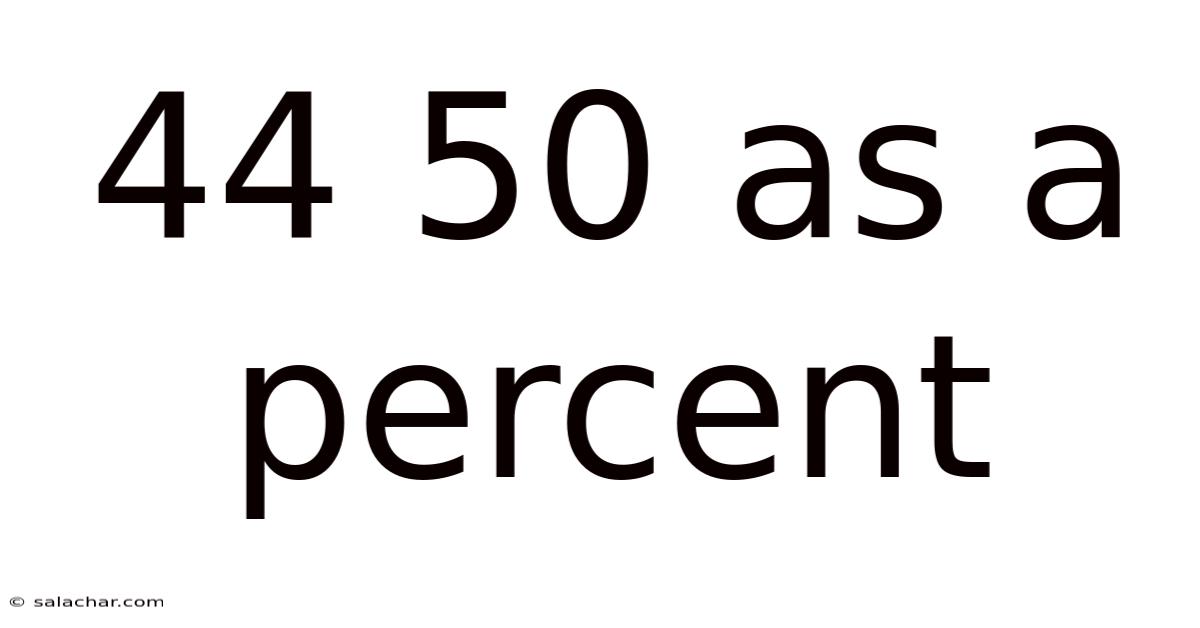
Table of Contents
Decoding 44/50 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill applicable across various fields, from everyday finances to advanced scientific calculations. This article provides a comprehensive guide on how to convert the fraction 44/50 into a percentage, explaining the underlying concepts and offering practical applications. We'll delve into the process step-by-step, explore different methods, and address common questions surrounding percentage calculations. By the end, you'll not only know the answer to "What is 44/50 as a percent?" but also possess a solid understanding of percentage conversions.
Understanding Percentages and Fractions
Before diving into the calculation, let's clarify the fundamental relationship between percentages, fractions, and decimals. A percentage represents a fraction out of 100. For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.50. Similarly, the fraction 44/50 represents 44 parts out of a total of 50 parts. To express this as a percentage, we need to convert it to an equivalent fraction with a denominator of 100.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is a common and straightforward method. We first convert the fraction 44/50 into a decimal by performing the division:
44 ÷ 50 = 0.88
Now, to convert the decimal 0.88 into a percentage, we multiply by 100:
0.88 × 100 = 88%
Therefore, 44/50 is equal to 88%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves manipulating the fraction to have a denominator of 100. We can achieve this by finding a number that, when multiplied by the original denominator (50), results in 100. In this case, that number is 2 (50 x 2 = 100). Crucially, whatever we do to the denominator, we must also do to the numerator to maintain the value of the fraction.
So, we multiply both the numerator and the denominator of 44/50 by 2:
(44 x 2) / (50 x 2) = 88/100
Since 88/100 represents 88 parts out of 100, this directly translates to 88%.
Method 3: Using Proportions
This method utilizes the concept of proportions. We can set up a proportion to solve for the percentage:
44/50 = x/100
To solve for x (the percentage), we cross-multiply:
44 x 100 = 50 x x
4400 = 50x
Now, divide both sides by 50:
x = 4400 ÷ 50 = 88
Therefore, x = 88, meaning 44/50 is 88%.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples:
-
Academic Performance: If a student answers 44 out of 50 questions correctly on a test, their score is 88%. This allows for easy comparison of performance across different tests or assignments.
-
Sales and Discounts: Stores often advertise discounts as percentages. For instance, a 20% discount on a $100 item means a reduction of $20 (20% of $100). Similar calculations are used to determine sales tax or profit margins.
-
Financial Calculations: Interest rates on loans or savings accounts are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Data Analysis: Percentages are frequently used to represent proportions in data analysis, making it easier to understand and interpret trends and patterns. For instance, if a survey shows 44 out of 50 respondents prefer a particular product, the percentage of preference can be easily communicated as 88%.
Further Exploration: Working with Different Fractions
The methods outlined above can be applied to any fraction you need to convert to a percentage. Let's consider a few examples:
-
Converting 25/50 to a percentage: Using the decimal method, 25 ÷ 50 = 0.50. Multiplying by 100 gives us 50%.
-
Converting 15/20 to a percentage: First, simplify the fraction to 3/4. Then convert to decimal: 3 ÷ 4 = 0.75. Multiplying by 100 gives us 75%.
-
Converting a fraction like 1/3 to a percentage: This will result in a recurring decimal (0.333...). Rounding to a suitable number of decimal places is often necessary. For example, 0.333... can be rounded to 0.33, giving us 33%.
Frequently Asked Questions (FAQ)
Q: Is there a quick way to calculate percentages without a calculator?
A: For simple fractions, mental math can often suffice. For example, knowing that 50% is half, you can quickly determine that 25/50 is 50%. For more complex fractions, estimation can be helpful.
Q: What if the denominator of the fraction isn't easily divisible to reach 100?
A: The decimal method remains reliable in these instances. You can still divide the numerator by the denominator to get a decimal and then multiply by 100 to obtain the percentage.
Q: How do I convert a percentage back to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 88% becomes 88/100, which simplifies to 22/25.
Q: Are there any online tools or calculators that can help with percentage conversions?
A: Yes, many online calculators can perform percentage conversions quickly and accurately. However, understanding the underlying principles remains crucial for problem-solving and comprehension.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with wide-ranging applications. This article has presented three different methods—using decimals, finding equivalent fractions, and employing proportions—each offering a clear pathway to accurate conversion. By understanding these methods and practicing them, you'll develop a strong foundation in percentage calculations, empowering you to tackle various mathematical and real-world problems with confidence. Remember, the key is not just knowing the answer (88% in this case), but understanding why and how we arrive at that answer. This deeper understanding is what truly unlocks the power of mathematical concepts.
Latest Posts
Latest Posts
-
Where Is Stratified Columnar Found
Sep 08, 2025
-
What Is 95 Of 60
Sep 08, 2025
-
Is Conductivity Physical Or Chemical
Sep 08, 2025
-
Is Naoh A Strong Base
Sep 08, 2025
-
Hard And Soft Acid Base
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 44 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.