5.25 As A Mixed Number
salachar
Sep 09, 2025 · 5 min read
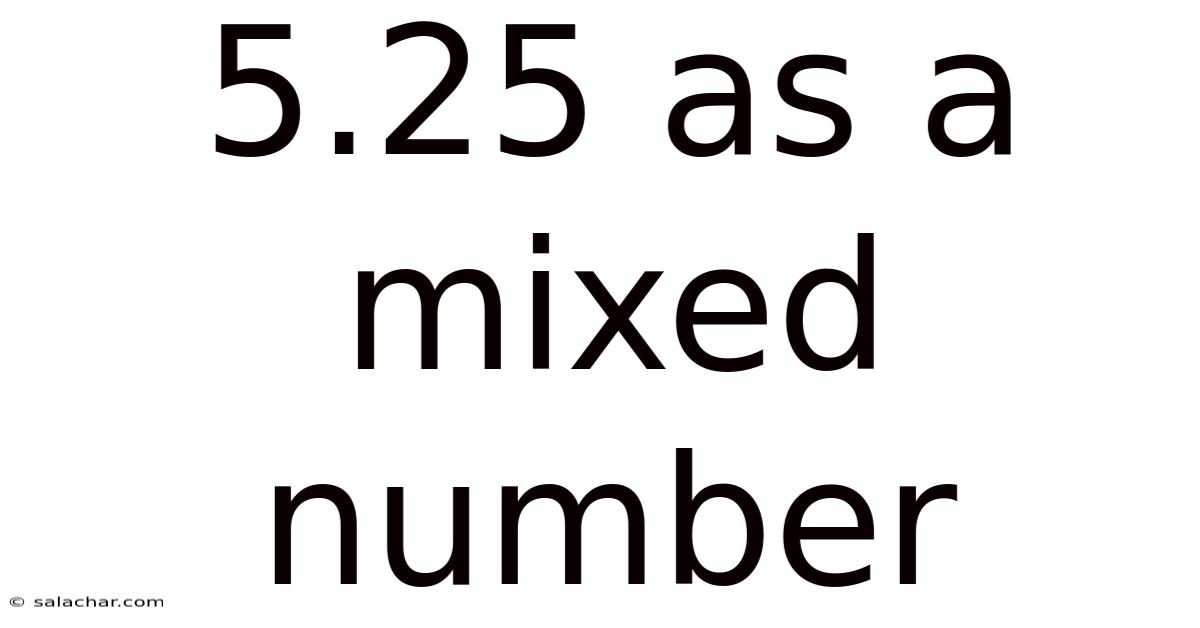
Table of Contents
Decoding 5.25: Understanding Mixed Numbers and Decimal Conversions
The seemingly simple decimal number 5.25 holds within it a world of mathematical concepts, particularly the relationship between decimals and mixed numbers. This article will delve deep into understanding 5.25 as a mixed number, explaining the process, the underlying principles, and providing further examples to solidify your grasp of this crucial mathematical skill. We'll explore not just the conversion itself, but also the broader implications of understanding fractions, decimals, and their inter-relationship.
Understanding Decimals and Mixed Numbers
Before we jump into converting 5.25, let's establish a firm understanding of the terms involved.
-
Decimal Numbers: These are numbers expressed using a base-ten system, with a decimal point separating the whole number part from the fractional part. The digits to the right of the decimal point represent fractions with denominators that are powers of 10 (tenths, hundredths, thousandths, etc.). For example, in 5.25, the '5' before the decimal represents 5 whole units, while '.25' represents 25 hundredths.
-
Mixed Numbers: These numbers combine a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). They represent a quantity that is greater than one whole unit. For example, 2 ¾ is a mixed number, representing two whole units and three-quarters of another unit.
-
Improper Fractions: Unlike proper fractions, improper fractions have a numerator that is greater than or equal to the denominator. For example, 11/4 is an improper fraction. Improper fractions can be converted to mixed numbers and vice versa.
Converting 5.25 to a Mixed Number: A Step-by-Step Guide
Converting 5.25 to a mixed number involves understanding the place value of the digits after the decimal point. Here's a step-by-step guide:
Step 1: Identify the Whole Number Part
The whole number part of 5.25 is simply 5. This will form the whole number component of our mixed number.
Step 2: Convert the Decimal Part to a Fraction
The decimal part of 5.25 is .25. To convert this to a fraction, we consider the place value of the last digit. The '5' is in the hundredths place, meaning the denominator of our fraction will be 100. The numerator will be the digits after the decimal point, which is 25. Therefore, .25 is equal to 25/100.
Step 3: Simplify the Fraction
The fraction 25/100 can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 25 and 100 is 25. Dividing both the numerator and denominator by 25, we get:
25 ÷ 25 = 1 100 ÷ 25 = 4
So, 25/100 simplifies to 1/4.
Step 4: Combine the Whole Number and the Simplified Fraction
Now, we combine the whole number part (5) and the simplified fraction (1/4) to create our mixed number: 5 ¼
Therefore, 5.25 expressed as a mixed number is 5 ¼.
Understanding the Mathematical Principles Involved
The conversion process relies on the fundamental principles of place value and fraction simplification. The place value system allows us to represent numbers efficiently, while fraction simplification ensures we express the fraction in its simplest form. Understanding these principles helps us not only convert decimals to mixed numbers but also perform other arithmetic operations involving fractions and decimals.
Further Examples and Practice
Let's practice converting more decimals to mixed numbers. Remember the key steps: identify the whole number, convert the decimal part to a fraction, simplify the fraction, and combine the whole number and the simplified fraction.
-
Example 1: Convert 3.75 to a mixed number.
- Whole number: 3
- Decimal part: .75 = 75/100
- Simplify: 75/100 = ¾ (GCD is 25)
- Mixed number: 3 ¾
-
Example 2: Convert 1.6 to a mixed number.
- Whole number: 1
- Decimal part: .6 = 6/10
- Simplify: 6/10 = 3/5 (GCD is 2)
- Mixed number: 1 ⅗
-
Example 3: Convert 8.125 to a mixed number.
- Whole number: 8
- Decimal part: .125 = 125/1000
- Simplify: 125/1000 = ⅛ (GCD is 125)
- Mixed number: 8 ⅛
Converting Mixed Numbers Back to Decimals
To reinforce your understanding, let's also look at the reverse process: converting a mixed number back to a decimal.
To convert a mixed number to a decimal, we first convert the fraction part to a decimal by dividing the numerator by the denominator. Then, we add the resulting decimal to the whole number part.
For instance, to convert 5 ¼ back to a decimal:
- Convert the fraction: 1 ÷ 4 = 0.25
- Add to the whole number: 5 + 0.25 = 5.25
Frequently Asked Questions (FAQ)
Q: What if the decimal part doesn't have an easily recognizable fraction equivalent?
A: If the decimal part doesn't simplify to a common fraction, you can leave it as a fraction. For example, if you had 2.333..., you would represent it as 2 ⅓ (approximately, as it's a repeating decimal). Or you could leave it as 2 + 333/1000. The level of simplification depends on the context and desired accuracy.
Q: Are there any shortcuts for converting decimals to mixed numbers?
A: While there aren't any significant shortcuts, recognizing common decimal-fraction equivalents (like .5 = ½, .25 = ¼, .75 = ¾) can speed up the process. Practice is key to building fluency.
Q: Why is it important to learn about converting decimals to mixed numbers?
A: This skill is crucial for a deeper understanding of mathematical concepts. It builds your ability to work with different number representations and strengthens your understanding of fractions, decimals, and their relationship. It's a foundation for more advanced mathematical operations and problem-solving.
Conclusion: Mastering Decimals and Mixed Numbers
Mastering the conversion between decimals and mixed numbers is a fundamental skill in mathematics. It requires a clear understanding of place value, fraction simplification, and the relationship between these two number systems. Through practice and understanding the underlying principles, you can confidently navigate these conversions and enhance your overall mathematical proficiency. Remember, the key is to break down the process step-by-step, and with consistent practice, you'll become proficient in converting decimals to mixed numbers and vice versa. This skill will not only help you in academic settings but also prove invaluable in various real-world applications.
Latest Posts
Latest Posts
-
The Donkey By G K Chesterton
Sep 09, 2025
-
Vinegar Is Soluble In Water
Sep 09, 2025
-
Formula For Hydrogen Sulfate Ion
Sep 09, 2025
-
Sodium Is Very Reactive Metal
Sep 09, 2025
-
Saanen Goat Milk Per Day
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 5.25 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.