75 Is What Of 125
salachar
Sep 10, 2025 · 5 min read
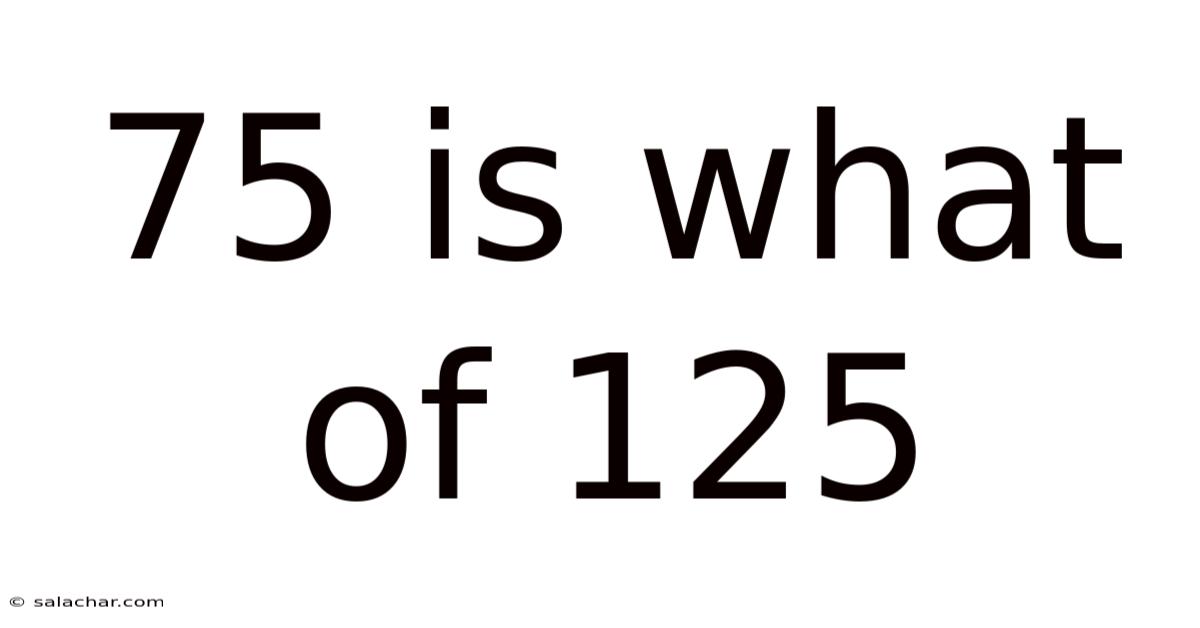
Table of Contents
75 is What Percent of 125? Understanding Percentages and Proportions
This article will thoroughly explore the question: "75 is what percent of 125?" We'll delve into the solution, explaining the underlying mathematical principles of percentages and proportions. Understanding percentages is crucial in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide will not only provide the answer but also equip you with the knowledge to solve similar problems independently. We'll cover multiple approaches, ensuring you grasp the concept fully, regardless of your current mathematical background.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" or "out of 100." When we say "x%," we mean x out of 100, or x/100. For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Percentages are used extensively to represent proportions or ratios. They are a valuable tool for comparing different quantities and making sense of data. Whether it's understanding sales tax, calculating interest rates, or analyzing changes in data, percentages provide a standardized way to express these relationships.
Solving "75 is What Percent of 125?" – Method 1: Using Proportions
The most straightforward way to solve this problem is by setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the proportion:
75/125 = x/100
Where 'x' represents the percentage we are trying to find. This proportion reads as: "75 is to 125 as x is to 100."
To solve for 'x', we can cross-multiply:
75 * 100 = 125 * x
7500 = 125x
Now, divide both sides by 125:
x = 7500 / 125
x = 60
Therefore, 75 is 60% of 125.
Solving "75 is What Percent of 125?" – Method 2: Using Decimal Conversion
Another approach involves converting the fraction 75/125 into a decimal and then multiplying by 100 to express it as a percentage.
First, divide 75 by 125:
75 ÷ 125 = 0.6
Next, multiply the decimal by 100 to convert it to a percentage:
0.6 * 100 = 60
Again, we find that 75 is 60% of 125. This method is often quicker for simpler problems.
Solving "75 is What Percent of 125?" – Method 3: The Formula Approach
A more generalized formula approach can be used to solve any "what percent of" problem. The formula is:
(Part / Whole) * 100 = Percentage
In our problem:
- Part = 75
- Whole = 125
Substituting these values into the formula:
(75 / 125) * 100 = 60
This confirms once again that 75 is 60% of 125. This formulaic approach is highly versatile and adaptable for various percentage calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in many everyday situations. Here are a few examples:
- Sales and Discounts: Stores often advertise discounts as percentages. For example, a 20% discount on a $100 item means you save $20 (20% of $100).
- Taxes: Sales tax, income tax, and other taxes are usually expressed as percentages.
- Tips and Gratuities: Calculating tips in restaurants often involves determining a percentage of the bill.
- Interest Rates: Understanding interest rates on loans, savings accounts, and investments requires working with percentages.
- Data Analysis: Percentages are used extensively in data analysis to compare proportions and trends. For example, analyzing market share often involves expressing different company's portion of the market as percentages.
- Grade Calculation: Many academic grading systems use percentages to represent a student's overall performance.
Further Exploring Percentages: Finding the Whole and the Part
While we've focused on finding the percentage, let's briefly look at how to find the whole or the part given the percentage and one of the other values.
Finding the Whole (given the part and percentage):
If we know that 75 is 60% of a certain number (the whole), we can set up the equation:
75 = 0.60 * x
Solving for x:
x = 75 / 0.60 = 125
Finding the Part (given the whole and percentage):
If we know that we want to find 60% of 125, the calculation is:
0.60 * 125 = 75
Frequently Asked Questions (FAQ)
Q: What if the numbers are decimals or fractions?
A: The methods outlined above work equally well with decimals and fractions. Simply perform the calculations using the decimal or fraction forms of the numbers.
Q: Are there online calculators for percentage calculations?
A: Yes, many online calculators are available to help with percentage calculations. These can be helpful for quick calculations or checking your work. However, understanding the underlying principles is crucial for problem-solving and application in various contexts.
Q: How do I deal with percentages greater than 100%?
A: Percentages greater than 100% simply mean that the part is larger than the whole. This situation arises frequently when comparing values over time or across different groups. For instance, if sales increased by 120%, it means the sales are now 220% of the original amount (100% + 120%).
Q: What are some common percentage calculation mistakes to avoid?
A: Common mistakes include:
- Incorrect order of operations: Remember to follow the order of operations (PEMDAS/BODMAS) when performing calculations.
- Misplacing the decimal point: Ensure you correctly handle decimal points when converting decimals to percentages and vice versa.
- Confusing the part and the whole: Always clearly identify the part and the whole in the problem.
Conclusion
This article has comprehensively explored the solution to "75 is what percent of 125?", providing three different methods for solving the problem and demonstrating the underlying mathematical principles. Understanding percentages is a fundamental skill with wide-ranging applications in various areas of life. By mastering these concepts and approaches, you'll be equipped to tackle percentage-related problems with confidence and improve your analytical abilities. Remember to practice regularly to solidify your understanding and build proficiency in this crucial mathematical area. The ability to confidently calculate and interpret percentages is a valuable asset that will serve you well in your academic and professional endeavors.
Latest Posts
Latest Posts
-
Adjectives To Describe A Cat
Sep 10, 2025
-
Electron Charge To Mass Ratio
Sep 10, 2025
-
De Jong Philosophical Text Nyt
Sep 10, 2025
-
A Fruit Beginning With E
Sep 10, 2025
-
What Acid React With Metals
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 75 Is What Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.