80 100 As A Percent
salachar
Sep 07, 2025 · 5 min read
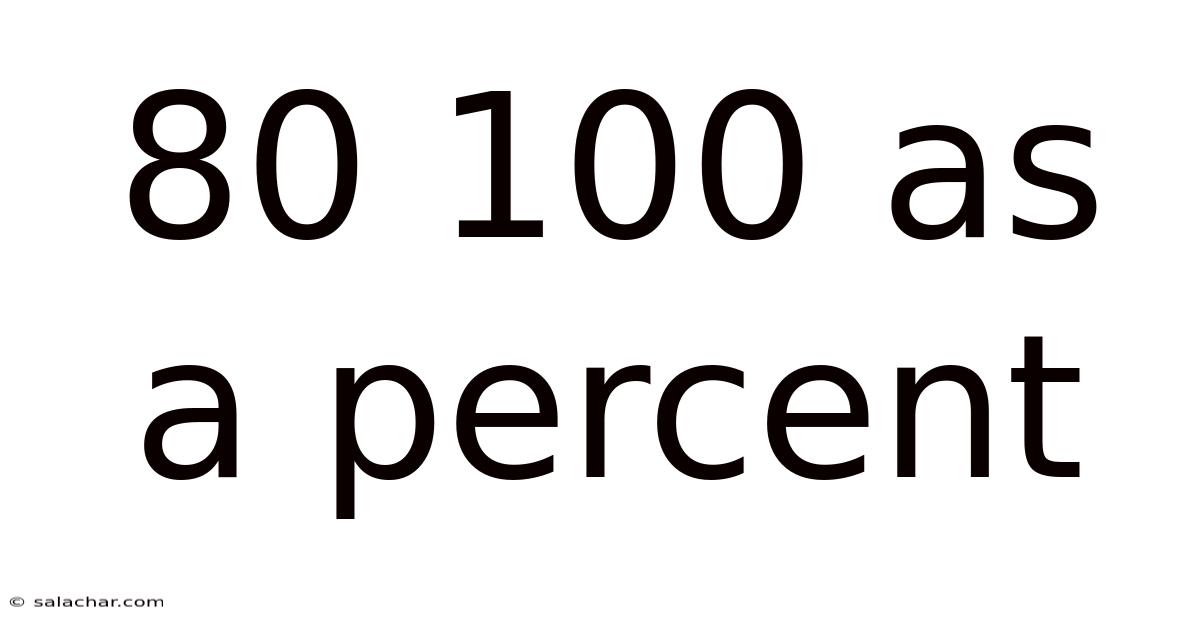
Table of Contents
Understanding 80/100 as a Percentage: A Comprehensive Guide
What does 80 out of 100 represent as a percentage? This seemingly simple question forms the basis for understanding percentages, a fundamental concept in mathematics and numerous real-world applications. This article will delve deep into calculating 80/100 as a percentage, exploring the underlying principles, practical examples, and addressing frequently asked questions. By the end, you'll not only know the answer but also possess a solid grasp of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a proportion relative to a whole, where the whole is always considered 100%.
For example, 50% means 50 out of 100, or 50/100. This is equivalent to the fraction ½ and the decimal 0.5. Understanding this foundational concept is crucial before tackling more complex percentage problems.
Calculating 80/100 as a Percentage
Calculating 80/100 as a percentage is straightforward. Since a percentage is a fraction out of 100, we can directly express 80/100 as a percentage:
80/100 = 80%
This means that 80 out of 100 represents 80 percent. It signifies that 80 parts out of a total of 100 parts are being considered.
Different Methods to Calculate Percentages
While the 80/100 example is simple, let's explore other methods for calculating percentages, which are useful when dealing with fractions that don't have a denominator of 100.
Method 1: Using the Fraction Method
This method involves converting the fraction to an equivalent fraction with a denominator of 100. If we have a fraction like 40/50, we can simplify it to 4/5 and then find an equivalent fraction with a denominator of 100:
- 4/5 = x/100
- To find x, we cross-multiply: 5x = 400
- Divide both sides by 5: x = 80
- Therefore, 40/50 = 80/100 = 80%
Method 2: Using Decimal Conversion
This involves converting the fraction to a decimal and then multiplying by 100 to get the percentage. Let's take the example of 3/4:
- Convert the fraction to a decimal: 3 ÷ 4 = 0.75
- Multiply the decimal by 100: 0.75 x 100 = 75%
- Therefore, 3/4 = 75%
Method 3: Using the Percentage Formula
The general formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
Let's say you scored 25 marks out of a total of 50 marks. Using the formula:
- (25 / 50) x 100% = 50%
This means you scored 50%.
Practical Applications of Percentages
Understanding percentages is crucial in various real-world scenarios:
-
Academic Performance: Calculating grades, test scores, and overall academic progress. A score of 80% on a test indicates a strong performance.
-
Finance: Calculating interest rates, discounts, taxes, and profit margins. Understanding percentage changes in investments is vital for financial planning.
-
Statistics: Representing data in a visually understandable way using charts and graphs. Percentages provide a standardized way to compare different datasets.
-
Sales and Marketing: Determining sales growth, market share, and advertising effectiveness. Discount percentages are essential for attracting customers.
-
Everyday Life: Calculating tips in restaurants, understanding sales discounts in stores, and comparing prices of different products.
Advanced Percentage Calculations
While 80/100 is a straightforward calculation, understanding more complex scenarios is valuable:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. For example, if a price increases from $50 to $60, the percentage increase is calculated as: [(60-50)/50] x 100% = 20%.
-
Calculating the Original Value: If you know the percentage and the final value, you can calculate the original value. For example, if a product is discounted by 20% and costs $80 after the discount, the original price was $100.
Examples of Real-World Applications of 80/100 (80%)
Let's consider some concrete examples illustrating the practical use of 80/100 or 80%:
-
Test Scores: A student achieving 80 out of 100 marks on a test has scored 80%, demonstrating a good understanding of the subject matter. This score might be considered a B or a high B-.
-
Completion Rate: A project with 80 tasks completed out of 100 is 80% complete. This allows for easy monitoring of progress and identification of any potential delays.
-
Survey Results: If 80 out of 100 respondents to a survey agree with a particular statement, this signifies strong agreement (80% approval rating).
-
Manufacturing Yield: A factory producing 80 functional products out of every 100 manufactured items has an 80% yield rate. This indicates efficiency and potential areas for improvement.
Frequently Asked Questions (FAQs)
Q1: How do I calculate a percentage if the denominator is not 100?
A1: Use one of the methods described above: the fraction method, decimal conversion, or the general percentage formula. Always divide the part by the whole and multiply by 100%.
Q2: What does it mean if a percentage is greater than 100%?
A2: A percentage greater than 100% means that the "part" is larger than the "whole." This often happens when comparing changes over time or when dealing with growth rates. For example, a 120% increase indicates that the value has more than doubled.
Q3: Can I use a calculator to calculate percentages?
A3: Yes, most calculators have a percentage function (%) that simplifies the calculation. Simply input the fraction and press the percentage button.
Q4: What are some common percentage errors to avoid?
A4: Common errors include incorrectly placing the decimal point, mixing up the "part" and the "whole" in the calculation, and not understanding the context of the percentage. Always double-check your work and ensure the calculation reflects the question being asked.
Conclusion
Understanding 80/100 as a percentage—80%—is fundamental to grasping the broader concept of percentages. This article has explored various methods of calculating percentages, discussed their wide-ranging applications, and answered common questions. Mastering percentage calculations is a vital skill applicable across numerous fields, empowering you to analyze data, interpret information, and make informed decisions in various aspects of life. Remember to practice regularly, using different methods to strengthen your understanding and build confidence in your ability to tackle percentage problems effectively. The ability to confidently work with percentages is a valuable asset in both academic and professional settings.
Latest Posts
Latest Posts
-
What Is Your Pointer Finger
Sep 07, 2025
-
Difference Between Excrete And Secrete
Sep 07, 2025
-
Role Of Credit For Development
Sep 07, 2025
-
Do Plant Cells Have Dna
Sep 07, 2025
-
Nand To And Gate Conversion
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 80 100 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.