Additive Inverse Of 2 3
salachar
Sep 13, 2025 · 6 min read
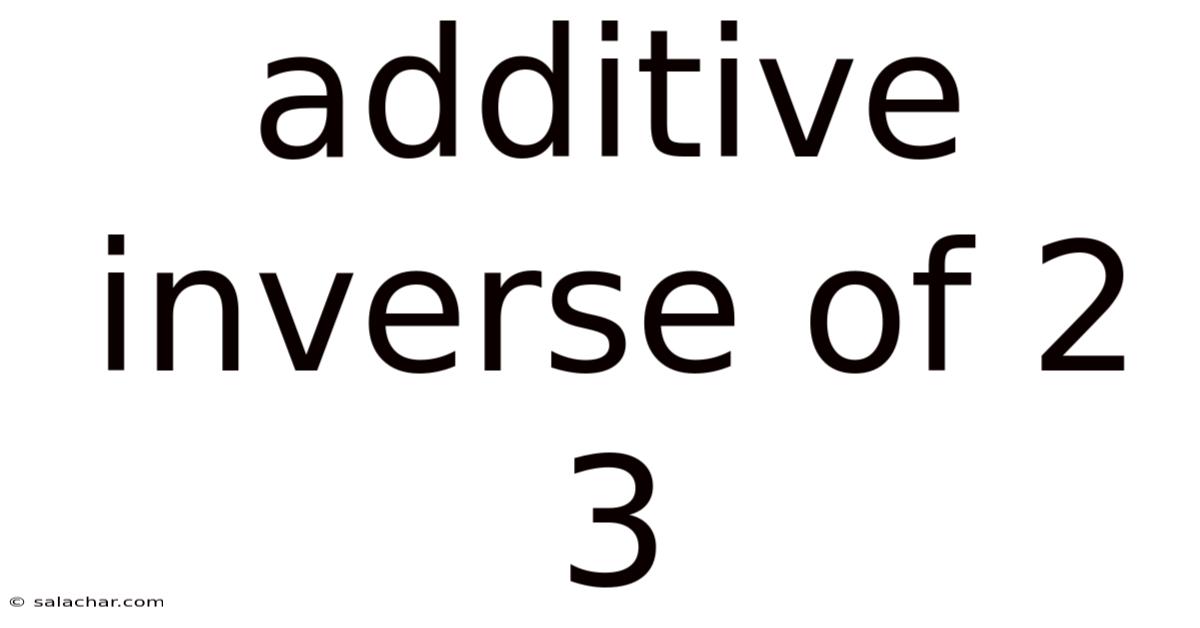
Table of Contents
Understanding the Additive Inverse: A Deep Dive into the Inverse of 2/3
The concept of additive inverse might seem daunting at first glance, especially when dealing with fractions like 2/3. But fear not! This comprehensive guide will break down the idea of additive inverses, explain how to find the additive inverse of 2/3, and explore the underlying mathematical principles. We'll delve into practical applications and even address some frequently asked questions to ensure a complete understanding of this fundamental concept in mathematics.
What is an Additive Inverse?
In simple terms, the additive inverse of a number is the number that, when added to the original number, results in a sum of zero. It's the "opposite" of a number. Think of it like this: if you're on a number line and you move a certain distance in one direction, the additive inverse represents moving the same distance in the opposite direction to get back to where you started (zero).
For example:
- The additive inverse of 5 is -5, because 5 + (-5) = 0.
- The additive inverse of -10 is 10, because -10 + 10 = 0.
- The additive inverse of 0 is 0, because 0 + 0 = 0.
Finding the Additive Inverse of 2/3
Now, let's apply this concept to the fraction 2/3. To find its additive inverse, we need to find a number that, when added to 2/3, equals zero. The answer is quite straightforward: the additive inverse of 2/3 is -2/3.
This is because:
2/3 + (-2/3) = 0
The process is simply changing the sign of the fraction. If the fraction is positive, its additive inverse is negative, and vice-versa.
A Deeper Look: Mathematical Principles
The concept of additive inverses is rooted in the properties of real numbers. Specifically, it relates to the following:
-
Additive Identity: Zero (0) is the additive identity. Adding zero to any number does not change the number's value. This is crucial because the additive inverse is defined by its ability to, when added to the original number, result in the additive identity (zero).
-
Closure Property of Addition: The sum of any two real numbers is always another real number. This ensures that the result of adding a number and its additive inverse (which is zero) remains within the set of real numbers.
-
Commutative Property of Addition: The order in which we add two numbers does not affect the sum. This means a + b = b + a. Therefore, 2/3 + (-2/3) is the same as (-2/3) + 2/3, both equaling zero.
-
Associative Property of Addition: The way we group numbers when adding multiple numbers does not affect the sum. This means (a + b) + c = a + (b + c). While not directly used in finding the additive inverse of a single number, this property becomes important when dealing with more complex additions involving additive inverses.
Additive Inverses in Different Number Systems
The concept of additive inverses extends beyond fractions and integers. It applies to all real numbers, including:
-
Integers: As seen earlier, the additive inverse of an integer is simply its negative counterpart.
-
Decimal Numbers: The additive inverse of a decimal number is its negative counterpart. For example, the additive inverse of 3.14 is -3.14.
-
Complex Numbers: Complex numbers have a real and an imaginary part (e.g., a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit, √-1). The additive inverse of a complex number is found by negating both its real and imaginary parts. For instance, the additive inverse of 2 + 3i is -2 - 3i.
Practical Applications of Additive Inverses
Understanding additive inverses is fundamental to many areas of mathematics and its applications:
-
Solving Equations: Additive inverses are essential for solving algebraic equations. To isolate a variable, we often add the additive inverse of a term to both sides of the equation. For example, to solve x + 2/3 = 1, we add -2/3 to both sides: x + 2/3 + (-2/3) = 1 + (-2/3), simplifying to x = 1/3.
-
Vector Addition: In physics and engineering, vectors represent quantities with both magnitude and direction. The additive inverse of a vector has the same magnitude but points in the opposite direction. Adding a vector to its additive inverse results in a zero vector (a vector with zero magnitude).
-
Calculus: Additive inverses play a role in various calculus concepts, such as finding limits and derivatives.
-
Linear Algebra: Additive inverses are crucial in linear algebra operations, especially when dealing with matrices and vectors.
Beyond the Basics: Exploring Related Concepts
Understanding additive inverses opens doors to exploring related mathematical concepts:
-
Multiplicative Inverse (Reciprocal): While the additive inverse results in zero when added, the multiplicative inverse (or reciprocal) results in one when multiplied. The multiplicative inverse of 2/3 is 3/2 because (2/3) * (3/2) = 1.
-
Inverse Functions: In the realm of functions, an inverse function essentially "undoes" the original function. The concept of inverses is closely related to additive and multiplicative inverses.
Frequently Asked Questions (FAQs)
Q: Is the additive inverse always negative?
A: No, the additive inverse of a negative number is positive. The additive inverse simply changes the sign of the number.
Q: Can a number have more than one additive inverse?
A: No, each number has only one additive inverse.
Q: What is the additive inverse of a fraction with a negative numerator and a negative denominator?
A: A fraction with a negative numerator and a negative denominator is positive overall. Its additive inverse will be negative. For example, the additive inverse of (-2)/(-3) (which simplifies to 2/3) is -2/3.
Q: How do I represent the additive inverse graphically?
A: On a number line, the additive inverse of a number is its reflection across zero. For example, the additive inverse of 2/3 would be plotted on the number line at -2/3.
Q: Is there a practical use for additive inverses in everyday life?
A: While not directly apparent in everyday activities, the principles underlying additive inverses are used implicitly in many situations involving balancing or canceling out quantities. For instance, in accounting, debits and credits (which can be viewed as additive inverses) are used to balance accounts.
Conclusion
Understanding the additive inverse, particularly in the context of fractions like 2/3, is a cornerstone of mathematical fluency. It's more than just a rule to memorize; it's a fundamental principle underpinning many mathematical operations and applications. By grasping this concept and exploring its related principles, you build a stronger foundation for tackling more complex mathematical problems. Remember, the additive inverse of 2/3 is simply -2/3, and understanding why this is the case provides a deeper understanding of the broader mathematical landscape. This exploration has equipped you not only to find the additive inverse of 2/3 but also to confidently approach similar problems and further explore the fascinating world of numbers and their properties.
Latest Posts
Latest Posts
-
Animals That Live In Freshwater
Sep 13, 2025
-
Sulfuric Acid And Ammonia Reaction
Sep 13, 2025
-
What Do Goosebumps Alnogy Meaning
Sep 13, 2025
-
Land Animals Without External Ears
Sep 13, 2025
-
What Is Divided By 16
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Additive Inverse Of 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.