Factor 2x 2 7x 15
salachar
Sep 09, 2025 · 6 min read
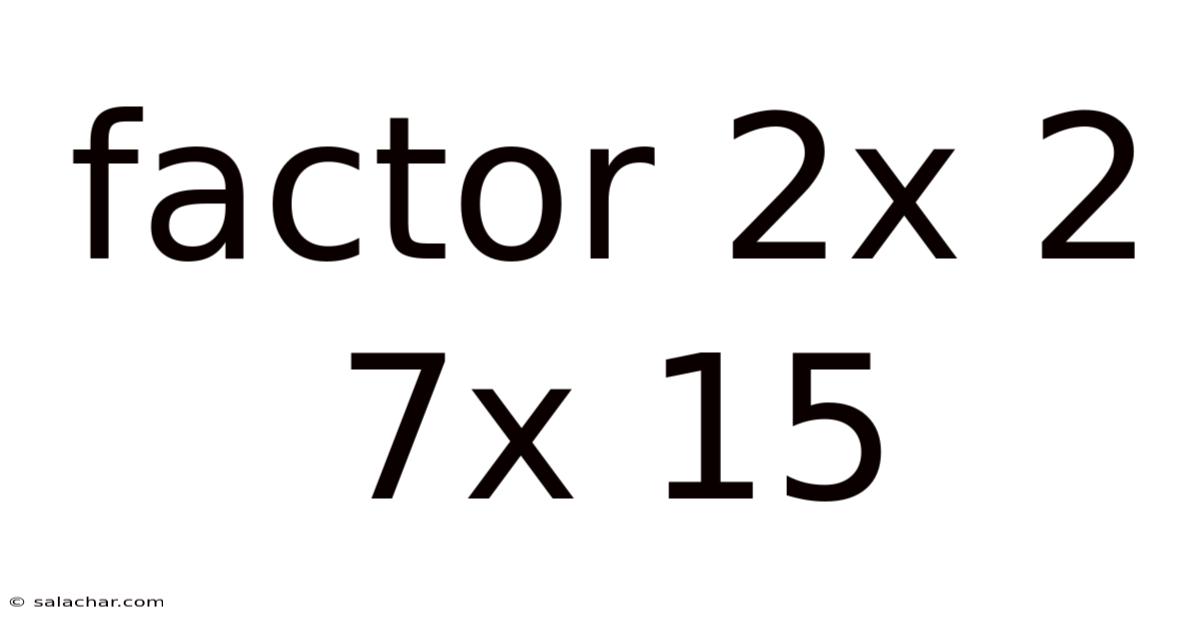
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 2x² + 7x + 15
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor allows you to solve quadratic equations, simplify complex expressions, and lay the groundwork for more advanced mathematical concepts. This article will provide a comprehensive guide on factoring the specific quadratic expression 2x² + 7x + 15, explaining the process step-by-step and exploring the underlying principles. We'll also delve into various methods and address common questions, equipping you with a solid understanding of this important algebraic technique.
Understanding Quadratic Expressions
Before we tackle the specific problem, let's review the basics. A quadratic expression is an algebraic expression of the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. The term 'quadratic' refers to the highest power of the variable 'x', which is 2. Factoring a quadratic expression means rewriting it as a product of two simpler expressions, typically two binomials. This process is the reverse of expanding binomials using the FOIL method (First, Outer, Inner, Last).
Our target expression is 2x² + 7x + 15. Here, a = 2, b = 7, and c = 15. Our goal is to find two binomials whose product equals this expression.
Method 1: Factoring by Trial and Error
This method involves systematically trying different combinations of binomial factors until we find the correct pair. It relies on understanding how the FOIL method works in reverse.
Remember, when we multiply two binomials (px + q)(rx + s), we get:
- First: px * rx = prx²
- Outer: px * s = psx
- Inner: q * rx = qrx
- Last: q * s = qs
The sum of the Outer and Inner terms gives us the 'bx' term in our quadratic expression (psx + qrx = bx), and the Last term gives us the 'c' term (qs = c).
Let's apply this to 2x² + 7x + 15:
-
Consider the factors of the leading coefficient (a = 2): The only factors of 2 are 1 and 2. This means our binomials will likely start with (x ) and (2x ).
-
Consider the factors of the constant term (c = 15): The factor pairs of 15 are (1, 15) and (3, 5).
-
Test the combinations: Let's try different combinations:
- (x + 1)(2x + 15) => Expanding this gives 2x² + 17x + 15 (Incorrect)
- (x + 15)(2x + 1) => Expanding this gives 2x² + 31x + 15 (Incorrect)
- (x + 3)(2x + 5) => Expanding this gives 2x² + 11x + 15 (Incorrect)
- (x + 5)(2x + 3) => Expanding this gives 2x² + 13x + 15 (Incorrect)
It seems none of these combinations work. Let's re-examine our approach. The issue is that we're focused solely on the constants. We need to consider the sum of the outer and inner products to equal 7x.
Let's try a more organized approach. We are looking for two numbers that:
- Multiply to equal (a * c) = (2 * 15) = 30
- Add to equal b = 7
The two numbers that fit these criteria are 3 and 10 (3 + 10 = 13, not 7, so this example doesn't factor nicely using this method, unlike many others). It seems that this quadratic expression doesn't factor nicely into whole numbers. This highlights that not all quadratic expressions can be factored using integers.
Method 2: The Quadratic Formula
When factoring by trial and error proves difficult or impossible using integers, the quadratic formula provides a reliable method for finding the roots of the quadratic equation ax² + bx + c = 0. The roots can then be used to factor the expression.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression 2x² + 7x + 15 = 0, we have: a = 2, b = 7, c = 15. Substituting these values into the formula:
x = [-7 ± √(7² - 4 * 2 * 15)] / (2 * 2) x = [-7 ± √(49 - 120)] / 4 x = [-7 ± √(-71)] / 4
Notice that we have a negative number under the square root. This means the roots are complex numbers (involving the imaginary unit 'i', where i² = -1). Therefore, the expression 2x² + 7x + 15 cannot be factored using real numbers.
Method 3: Completing the Square
Completing the square is another technique for solving quadratic equations and can sometimes be used to help factor expressions. However, it's often more complex than the quadratic formula for this specific purpose.
Why This Quadratic Doesn't Factor Nicely with Integers
The reason 2x² + 7x + 15 doesn't factor neatly using integers is related to the discriminant (the expression inside the square root in the quadratic formula: b² - 4ac). In this case, the discriminant is -71, which is negative. A negative discriminant indicates that the quadratic equation has no real roots, meaning the quadratic expression cannot be factored into linear factors with real coefficients.
Conclusion
While we initially attempted to factor 2x² + 7x + 15 using trial and error, we discovered that this expression cannot be factored into linear expressions with real number coefficients. This is because the discriminant of the corresponding quadratic equation is negative. The quadratic formula confirmed this, revealing complex roots. This highlights the importance of understanding multiple methods for solving quadratic equations and recognizing when a quadratic expression is not factorable using real numbers. Sometimes, the simplest solution is to leave the expression as it is, acknowledging that it's a prime quadratic expression in the context of real numbers.
Frequently Asked Questions (FAQs)
Q1: What does it mean for a quadratic to be "prime"?
A1: A prime quadratic expression is one that cannot be factored into linear factors with real coefficients. It's analogous to a prime number, which cannot be factored into smaller integers.
Q2: Are there other ways to express this quadratic?
A2: While it cannot be factored using real numbers, you could express it in its vertex form by completing the square, or you could use the quadratic formula to find its roots and express it in terms of those roots. However, these methods don't result in a simpler factored form in the way we initially attempted.
Q3: Is it always necessary to factor a quadratic?
A3: No, factoring is a useful technique for simplification and solving equations, but it's not always necessary or possible. Other methods, such as the quadratic formula or completing the square, can be used to solve quadratic equations or work with quadratic expressions in different contexts.
Q4: What if I encounter a similar problem in the future?
A4: Always start with attempting factoring by trial and error. If that fails, use the quadratic formula to check for real roots. If the discriminant is negative, the quadratic is prime (in the real number system). Remember that not all quadratics are easily factored.
This detailed explanation provides a thorough understanding of factoring quadratic expressions, highlighting the importance of multiple methods and the limitations of factoring with real numbers. The example of 2x² + 7x + 15 serves as a valuable case study demonstrating that not every quadratic expression can be factored simply. The focus on a single, specific problem allows for an in-depth exploration of different techniques and their applications.
Latest Posts
Latest Posts
-
Fun Facts About Howler Monkeys
Sep 09, 2025
-
Is Cos Polar Or Nonpolar
Sep 09, 2025
-
Fruits Starting With Letter C
Sep 09, 2025
-
Bicuspid Vs Tricuspid Aortic Valve
Sep 09, 2025
-
Monatomic Ions And Polyatomic Ions
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 7x 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.