Factor X 2 8x 12
salachar
Sep 10, 2025 · 6 min read
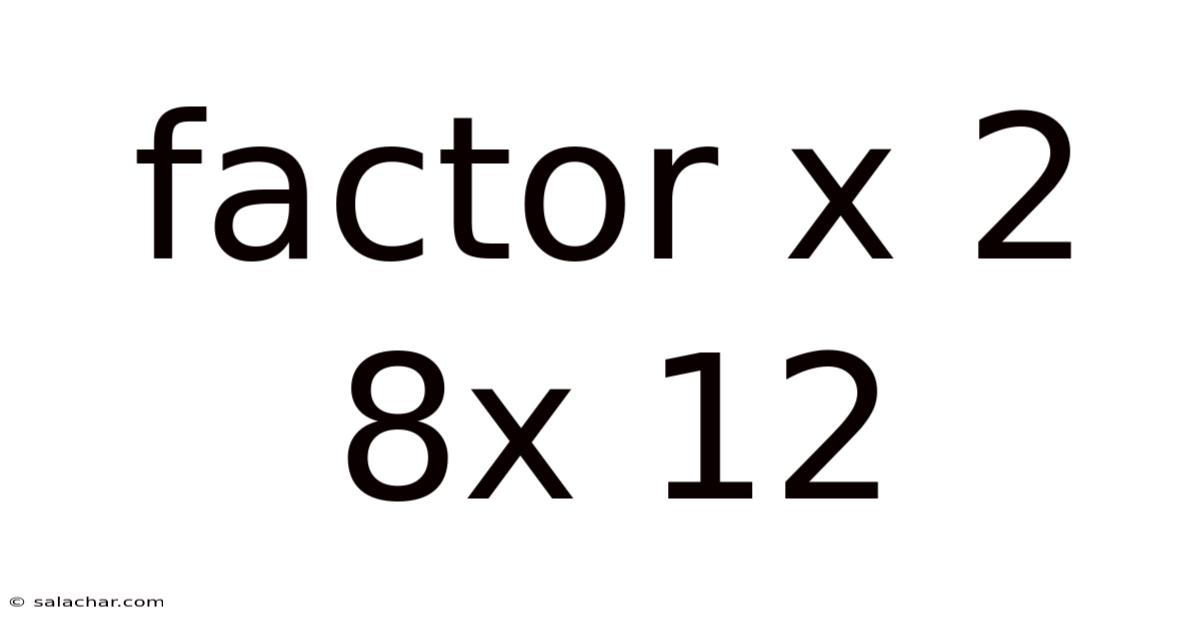
Table of Contents
Unraveling the Mystery: A Deep Dive into the Quadratic Expression x² + 8x + 12
Understanding quadratic expressions is fundamental to success in algebra and beyond. This seemingly simple expression, x² + 8x + 12, serves as an excellent example to explore the various methods for solving and interpreting quadratic equations. This article will delve into the intricacies of this specific expression, covering factorization, the quadratic formula, graphing, and real-world applications, ensuring a comprehensive understanding for students of all levels.
Introduction: What Makes x² + 8x + 12 Special?
The expression x² + 8x + 12 is a quadratic trinomial, meaning it's a polynomial with three terms and the highest power of the variable (x) is 2. Understanding how to manipulate and solve quadratic expressions like this is crucial for tackling more complex mathematical problems in fields ranging from physics and engineering to finance and computer science. This article will equip you with the tools and knowledge necessary to confidently handle similar expressions. We will explore different methods to factor this expression, understand its graphical representation, and even touch upon its application in solving real-world problems.
Method 1: Factoring the Quadratic Expression
Factoring is the process of breaking down a polynomial expression into simpler expressions that, when multiplied together, give the original expression. This is often the most efficient method for solving quadratic equations, especially when the factors are relatively easy to identify. For x² + 8x + 12, we look for two numbers that add up to 8 (the coefficient of x) and multiply to 12 (the constant term).
Those two numbers are 6 and 2. Therefore, we can factor x² + 8x + 12 as follows:
(x + 6)(x + 2)
To verify this factorization, we can expand the expression using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * 2 = 2x
- Inner: 6 * x = 6x
- Last: 6 * 2 = 12
Adding these terms together, we get x² + 2x + 6x + 12 = x² + 8x + 12, confirming our factorization.
Method 2: Completing the Square
Completing the square is a powerful technique for solving quadratic equations, especially when factoring isn't immediately apparent. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Let's apply this method to x² + 8x + 12:
-
Isolate the x terms: We start by isolating the terms containing x: x² + 8x = -12
-
Complete the square: To complete the square, we take half of the coefficient of x (which is 8/2 = 4), square it (4² = 16), and add it to both sides of the equation:
x² + 8x + 16 = -12 + 16
-
Factor the perfect square trinomial: The left side is now a perfect square trinomial:
(x + 4)² = 4
-
Solve for x: Take the square root of both sides:
x + 4 = ±2
This gives us two possible solutions:
x = -4 + 2 = -2 x = -4 - 2 = -6
These solutions correspond to the factors we found earlier: (x + 2) and (x + 6). The values of x that make the expression equal to zero are -2 and -6.
Method 3: Using the Quadratic Formula
The quadratic formula is a universal method for solving any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression, x² + 8x + 12 = 0, we have a = 1, b = 8, and c = 12. Substituting these values into the quadratic formula, we get:
x = [-8 ± √(8² - 4 * 1 * 12)] / (2 * 1) x = [-8 ± √(64 - 48)] / 2 x = [-8 ± √16] / 2 x = [-8 ± 4] / 2
This gives us the same two solutions as before:
x = (-8 + 4) / 2 = -2 x = (-8 - 4) / 2 = -6
Graphical Representation: Visualizing the Quadratic
The quadratic expression x² + 8x + 12 can be represented graphically as a parabola. The parabola opens upwards because the coefficient of x² (a) is positive. The x-intercepts of the parabola represent the roots (solutions) of the equation x² + 8x + 12 = 0. In our case, the x-intercepts are at x = -2 and x = -6. The y-intercept is found by setting x = 0, which gives us a y-intercept of 12. The vertex of the parabola (the lowest point) lies at the midpoint between the x-intercepts, which is x = -4. Substituting x = -4 into the expression gives a y-value of -4. Therefore, the vertex is at (-4, -4). This graphical representation provides a visual understanding of the behavior of the quadratic expression.
Real-World Applications: Where do we use this?
Quadratic equations have numerous applications in real-world scenarios. They can model projectile motion, the area of shapes, and various optimization problems.
For example:
-
Area Calculation: Imagine designing a rectangular garden with an area of 12 square meters and a perimeter of 14 meters. Letting x represent the width of the garden, the length would be (7-x) given that the perimeter is 2(x+(7-x)) = 14. The area would be expressed as x(7-x) = 12 which simplifies to x² - 7x + 12 = 0. Solving this equation (using any of the methods discussed above) would give you the dimensions of the garden.
-
Projectile Motion: The height of a projectile launched vertically can often be modeled using a quadratic equation. Understanding the roots of the equation helps determine when the projectile hits the ground.
-
Optimization Problems: Businesses frequently use quadratic equations to model profit, revenue, and cost functions. Finding the maximum or minimum point of a quadratic function is crucial for optimizing these factors.
Frequently Asked Questions (FAQ)
-
What is the difference between factoring and solving a quadratic equation? Factoring expresses the quadratic expression as a product of simpler expressions. Solving involves finding the values of x that make the expression equal to zero. Factoring is a method often used to solve quadratic equations.
-
Can all quadratic equations be factored easily? No, some quadratic equations have roots that are irrational or complex numbers, making factoring difficult or impossible using simple integer factors. In such cases, the quadratic formula or completing the square are more reliable methods.
-
Why is the quadratic formula so important? The quadratic formula is a powerful tool because it provides a solution for any quadratic equation, regardless of whether it's easily factorable or not. It's a universal method for solving these types of equations.
-
What does the discriminant (b² - 4ac) tell us? The discriminant in the quadratic formula determines the nature of the roots. If the discriminant is positive, there are two distinct real roots. If it's zero, there's one real root (a repeated root), and if it's negative, there are two complex roots.
Conclusion: Mastering Quadratic Expressions
The seemingly simple expression x² + 8x + 12 offers a rich opportunity to explore various techniques for understanding and solving quadratic equations. From factoring and completing the square to the universal application of the quadratic formula, each method provides valuable insights into the behavior and solutions of quadratic expressions. Understanding these methods is crucial not only for academic success but also for applying these concepts to solve a wide range of real-world problems in diverse fields. The ability to confidently manipulate and interpret quadratic expressions is a cornerstone of mathematical proficiency and problem-solving skills. By mastering these techniques, you're equipping yourself with a powerful set of tools applicable to numerous mathematical and scientific endeavors.
Latest Posts
Latest Posts
-
Plaster Of Paris Wall Art
Sep 10, 2025
-
Why Is Electron Affinity Negative
Sep 10, 2025
-
Waters Boiling Point In Kelvin
Sep 10, 2025
-
60 Minutes How Many Seconds
Sep 10, 2025
-
How Much Is 6 Nickels
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 8x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.