Gcf Of 35 And 20
salachar
Sep 08, 2025 · 6 min read
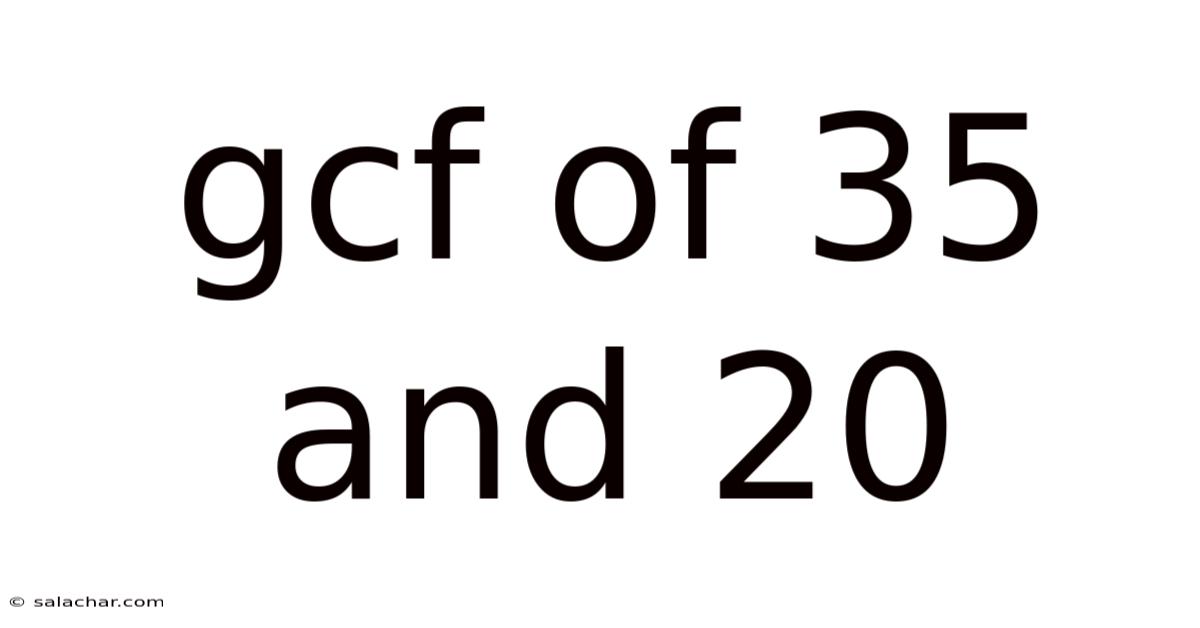
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 35 and 20: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles and exploring different methods for calculating the GCF opens doors to a deeper appreciation of number theory and its applications in various fields, from cryptography to computer science. This article will delve into the GCF of 35 and 20, explaining multiple approaches and illustrating the broader mathematical concepts involved. We'll cover everything from basic methods suitable for beginners to more advanced techniques, ensuring a comprehensive understanding for readers of all levels.
Understanding the Concept of Greatest Common Factor (GCF)
Before we tackle the specific case of 35 and 20, let's establish a solid foundation. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding this concept is crucial for various mathematical operations and problem-solving scenarios.
Method 1: Listing Factors
This is the most straightforward method, particularly useful for smaller numbers like 35 and 20. We start by listing all the factors of each number:
Factors of 35: 1, 5, 7, 35
Factors of 20: 1, 2, 4, 5, 10, 20
Now, we identify the common factors – the numbers that appear in both lists:
Common Factors: 1, 5
The greatest among these common factors is 5. Therefore, the GCF of 35 and 20 is 5.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the numbers' structure. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 35: 5 x 7
Prime Factorization of 20: 2 x 2 x 5 (or 2² x 5)
Now, we identify the common prime factors and their lowest powers. Both numbers share a single factor of 5. Therefore, the GCF is 5. This method highlights the fundamental building blocks of the numbers and allows for a more systematic approach, especially when dealing with larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger integers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 35 and 20:
- Divide the larger number (35) by the smaller number (20): 35 ÷ 20 = 1 with a remainder of 15.
- Replace the larger number (35) with the remainder (15): Now we find the GCF of 20 and 15.
- Divide the larger number (20) by the smaller number (15): 20 ÷ 15 = 1 with a remainder of 5.
- Replace the larger number (20) with the remainder (5): Now we find the GCF of 15 and 5.
- Divide the larger number (15) by the smaller number (5): 15 ÷ 5 = 3 with a remainder of 0.
Since the remainder is 0, the GCF is the last non-zero remainder, which is 5. The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers where listing factors would be impractical.
Illustrative Applications of GCF
The concept of GCF extends beyond simple arithmetic exercises. It finds practical applications in various fields:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 20/35 can be simplified by dividing both the numerator and denominator by their GCF, which is 5, resulting in the simplified fraction 4/7.
-
Geometry and Measurement: GCF is used in solving problems related to area and perimeter calculations, particularly when dealing with rectangles or other shapes with integer dimensions. For instance, finding the largest square tile that can perfectly cover a rectangular floor requires calculating the GCF of the floor's length and width.
-
Cryptography: GCF plays a vital role in cryptography, especially in RSA encryption, a widely used public-key cryptosystem. The security of RSA relies on the difficulty of finding the GCF of two very large numbers.
-
Computer Science: The Euclidean algorithm, used to find the GCF, is a fundamental algorithm in computer science, used in various applications including modular arithmetic and cryptography. Its efficiency makes it suitable for use in software and hardware implementations.
Beyond Two Numbers: Extending the Concept
The GCF concept isn't limited to just two numbers. We can extend it to find the GCF of three or more integers. One approach is to find the GCF of two numbers, and then find the GCF of the result and the next number, and so on. For example, to find the GCF of 12, 18, and 30:
- Find the GCF of 12 and 18: This is 6.
- Find the GCF of 6 and 30: This is 6.
Therefore, the GCF of 12, 18, and 30 is 6.
Frequently Asked Questions (FAQs)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, it means that the numbers are relatively prime or coprime. This signifies that they share no common factors other than 1.
Q2: Can the GCF of two numbers be larger than the smaller number?
A2: No. The GCF can never be larger than the smaller of the two numbers. It is, by definition, a common factor, and a factor cannot be larger than the number itself.
Q3: Is there a formula to calculate the GCF?
A3: There isn't a single, direct formula to calculate the GCF for all pairs of numbers. However, the methods described above (listing factors, prime factorization, and the Euclidean algorithm) provide systematic approaches to find the GCF. For specific cases, formulas might be derived, but general formulas are not available.
Q4: How can I use a calculator or computer to find the GCF?
A4: Many calculators and computer software packages include functions or commands for calculating the GCF (often denoted as GCD). Check your calculator's manual or the documentation for your software to learn how to use these functions.
Conclusion
Finding the GCF of 35 and 20, as explored through various methods, is more than just a simple arithmetic exercise. It serves as a gateway to understanding fundamental concepts in number theory, highlighting the importance of prime factorization and the efficiency of algorithms like the Euclidean algorithm. The ability to calculate the GCF is valuable not only in mathematical problem-solving but also in various fields that rely on mathematical principles. By understanding these methods and their underlying principles, we can appreciate the elegance and practicality of number theory in a broader context. The seemingly simple problem of finding the GCF of 35 and 20 thus opens a door to a richer understanding of the mathematical world around us.
Latest Posts
Latest Posts
-
What Is 42c In F
Sep 08, 2025
-
What Is 40 Of 12000
Sep 08, 2025
-
What Is Plural For Sheep
Sep 08, 2025
-
What Is 289 Square Root
Sep 08, 2025
-
Sound Is Produced By What
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 35 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.