Gcf Of 35 And 25
salachar
Sep 06, 2025 · 6 min read
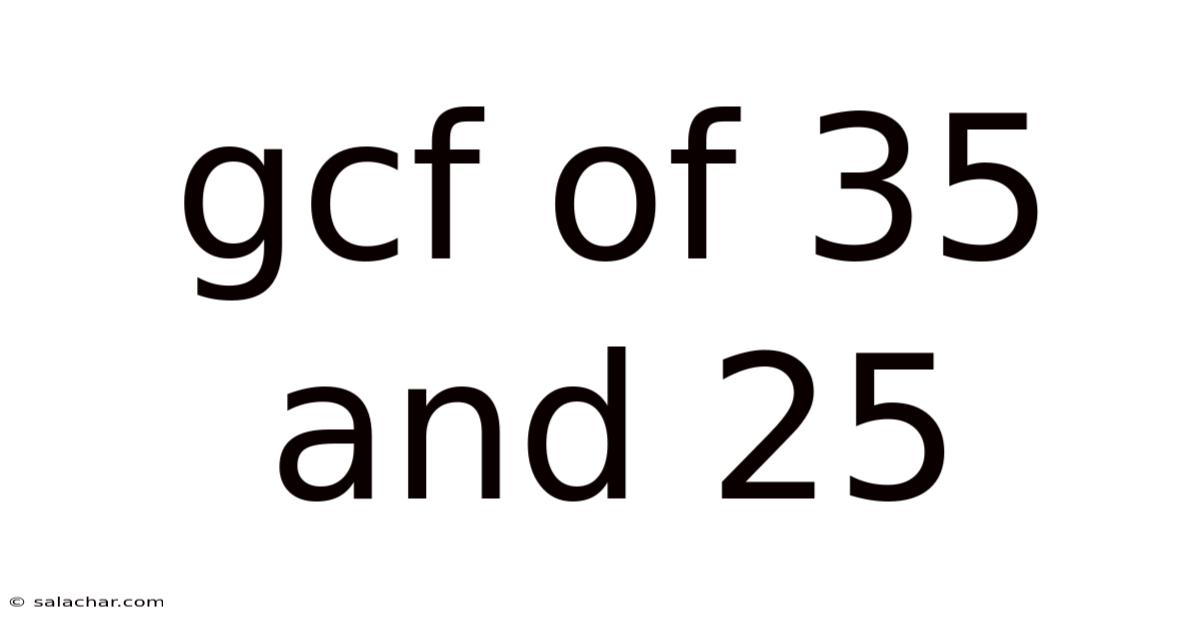
Table of Contents
Finding the Greatest Common Factor (GCF) of 35 and 25: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and tackling more advanced mathematical problems. This comprehensive guide will explore various methods for determining the GCF of 35 and 25, providing a deep dive into the underlying principles and practical applications. We'll not only find the GCF but also explore the broader implications of this mathematical concept.
Understanding Greatest Common Factor (GCF)
Before we delve into finding the GCF of 35 and 25, let's solidify our understanding of the term itself. The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest among these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
The most straightforward method to find the GCF is by listing all the factors of each number and identifying the largest common factor. Let's apply this method to find the GCF of 35 and 25.
Factors of 35: 1, 5, 7, 35
Factors of 25: 1, 5, 25
Common Factors: 1, 5
The largest common factor is 5. Therefore, the GCF of 35 and 25 is 5.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the GCF of larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on.
Let's find the prime factorization of 35 and 25:
- 35: 5 x 7
- 25: 5 x 5
Now, identify the common prime factors. Both numbers share a single factor of 5. To find the GCF, multiply the common prime factors together. In this case, the GCF is simply 5.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 35 and 25:
- Subtract the smaller number from the larger number: 35 - 25 = 10
- Replace the larger number with the result (10), and keep the smaller number (25): Now we find the GCF of 25 and 10.
- Subtract the smaller number from the larger number: 25 - 10 = 15
- Replace the larger number with the result (15), and keep the smaller number (10): Now we find the GCF of 15 and 10.
- Subtract the smaller number from the larger number: 15 - 10 = 5
- Replace the larger number with the result (5), and keep the smaller number (10): Now we find the GCF of 10 and 5.
- Subtract the smaller number from the larger number: 10 - 5 = 5
- The numbers are now 5 and 5. Therefore, the GCF is 5.
The Euclidean algorithm provides a systematic approach, especially helpful when dealing with larger numbers where listing factors becomes cumbersome.
Mathematical Implications and Applications of GCF
The concept of GCF extends far beyond simply finding the largest common factor of two numbers. It has significant applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. By dividing both the numerator and denominator by their GCF, we obtain an equivalent fraction in its simplest form. For example, the fraction 25/35 can be simplified by dividing both the numerator and denominator by their GCF, which is 5, resulting in the simplified fraction 5/7.
-
Least Common Multiple (LCM): The GCF is closely related to the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is divisible by both numbers. The relationship between GCF and LCM is given by the formula: LCM(a, b) x GCF(a, b) = a x b. This formula allows us to calculate the LCM if we know the GCF, and vice-versa.
-
Algebra: GCF plays a crucial role in factoring algebraic expressions. Factoring involves expressing an algebraic expression as a product of simpler expressions. Finding the GCF of the terms in an expression allows us to factor out the common factor, simplifying the expression.
-
Number Theory: The GCF is a fundamental concept in number theory, a branch of mathematics that deals with the properties of integers. It is used in various number-theoretic problems, including solving Diophantine equations and studying the distribution of prime numbers.
-
Real-World Applications: Beyond the realm of pure mathematics, the GCF finds applications in various real-world scenarios. For instance, it can be used to divide a collection of items into equal groups, determine the maximum size of identical squares that can be used to tile a rectangle, or solve problems related to scheduling and resource allocation.
Frequently Asked Questions (FAQ)
Q: What is the difference between GCF and LCM?
A: The GCF (Greatest Common Factor) is the largest number that divides both numbers without a remainder. The LCM (Least Common Multiple) is the smallest number that both numbers divide into without a remainder.
Q: Can the GCF of two numbers be 1?
A: Yes, if two numbers are relatively prime (meaning they share no common factors other than 1), their GCF is 1.
Q: How do I find the GCF of more than two numbers?
A: You can extend any of the methods described above to find the GCF of more than two numbers. For example, using prime factorization, find the prime factorization of each number, then identify the common prime factors and multiply them together. The Euclidean algorithm can also be adapted for multiple numbers.
Conclusion
Finding the greatest common factor of 35 and 25, as demonstrated through various methods, highlights the fundamental importance of this concept in mathematics. Whether employing the simple method of listing factors, the elegant approach of prime factorization, or the efficient Euclidean algorithm, understanding the GCF provides a solid foundation for tackling more complex mathematical problems across various disciplines. The applications of GCF extend beyond theoretical mathematics, finding practical use in simplifying fractions, factoring algebraic expressions, and solving real-world problems related to division, resource allocation, and scheduling. Mastering the concept of GCF is a key step in developing a strong mathematical foundation. Remember to choose the method that best suits your needs and the complexity of the numbers involved. Understanding the different approaches will allow you to tackle GCF problems with confidence and efficiency.
Latest Posts
Latest Posts
-
Difference Between Spermatogenesis And Oogenesis
Sep 07, 2025
-
Bank Account Closed Letter Format
Sep 07, 2025
-
Lewis Dot Structure Of Bef2
Sep 07, 2025
-
What Is Xi In Stats
Sep 07, 2025
-
B At 32c For Water
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 35 And 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.