Gcf Of 54 And 72
salachar
Sep 08, 2025 · 5 min read
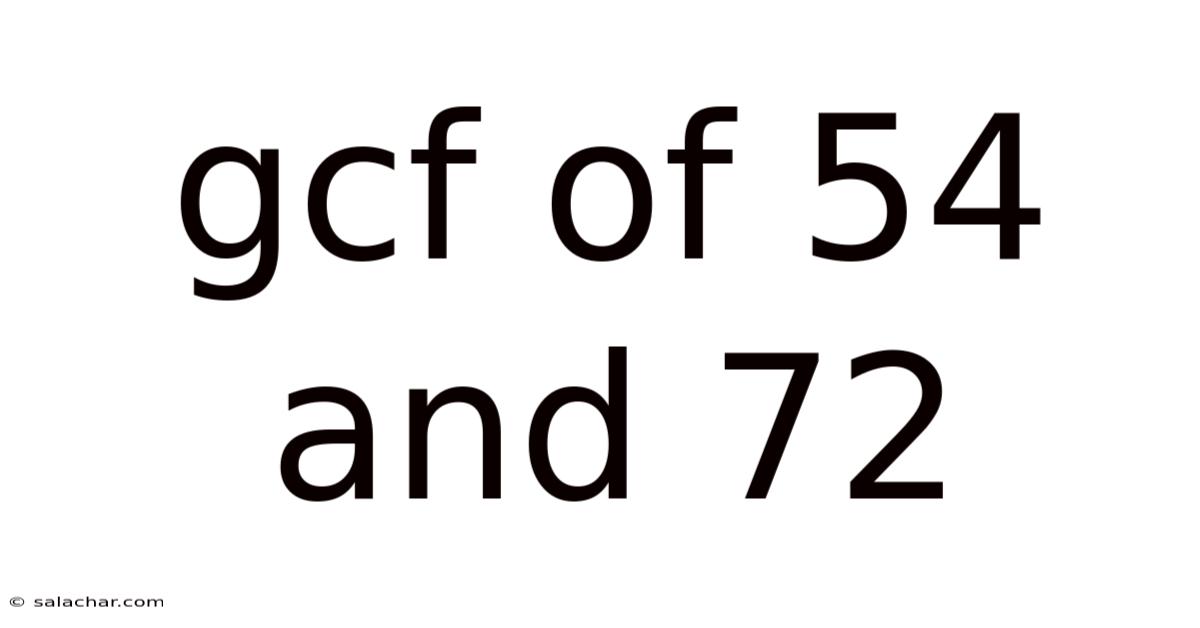
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 54 and 72: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving complex algebraic equations. This comprehensive guide will explore various methods to determine the GCF of 54 and 72, delve into the underlying mathematical principles, and provide practical examples to solidify your understanding. We will also explore the broader significance of GCFs in different mathematical contexts.
Understanding the Concept of Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. Understanding GCFs is crucial for simplifying fractions, solving problems involving ratios and proportions, and various other mathematical applications.
Method 1: Prime Factorization Method
This method is considered the most fundamental approach for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Step 1: Find the prime factorization of 54.
54 can be factored as follows: 54 = 2 x 27 = 2 x 3 x 9 = 2 x 3 x 3 x 3 = 2 x 3³.
-
Step 2: Find the prime factorization of 72.
72 can be factored as follows: 72 = 2 x 36 = 2 x 2 x 18 = 2 x 2 x 2 x 9 = 2 x 2 x 2 x 3 x 3 = 2³ x 3².
-
Step 3: Identify common prime factors.
Both 54 and 72 share the prime factors 2 and 3.
-
Step 4: Determine the lowest power of each common prime factor.
The lowest power of 2 is 2¹ (or simply 2) and the lowest power of 3 is 3².
-
Step 5: Multiply the lowest powers of the common prime factors.
GCF(54, 72) = 2¹ x 3² = 2 x 9 = 18
Therefore, the greatest common factor of 54 and 72 is 18.
Method 2: Listing Factors Method
This method is more suitable for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
-
Step 1: List all the factors of 54.
Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
-
Step 2: List all the factors of 72.
Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
-
Step 3: Identify common factors.
Common factors of 54 and 72: 1, 2, 3, 6, 9, 18
-
Step 4: Determine the greatest common factor.
The greatest common factor is 18.
This method, while straightforward, can become cumbersome with larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
-
Step 1: Start with the larger number (72) and the smaller number (54).
-
Step 2: Divide the larger number by the smaller number and find the remainder.
72 ÷ 54 = 1 with a remainder of 18
-
Step 3: Replace the larger number with the smaller number (54) and the smaller number with the remainder (18).
-
Step 4: Repeat the process.
54 ÷ 18 = 3 with a remainder of 0
-
Step 5: The GCF is the last non-zero remainder.
Since the remainder is 0, the GCF is the previous remainder, which is 18.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers.
Illustrative Examples and Applications
Let's explore how finding the GCF of 54 and 72 can be applied in practical situations.
-
Simplifying Fractions: If you have the fraction 54/72, finding the GCF (18) allows you to simplify it to its simplest form: 54/72 = (54 ÷ 18) / (72 ÷ 18) = 3/4.
-
Ratio and Proportion Problems: If you have a ratio of 54:72, simplifying it using the GCF (18) gives you a simpler equivalent ratio of 3:4.
-
Geometry Problems: Imagine you have a rectangular piece of land with dimensions 54 meters by 72 meters. You want to divide it into identical square plots. The side length of the largest possible square plot would be the GCF of 54 and 72, which is 18 meters.
Mathematical Significance and Advanced Concepts
The concept of the GCF extends beyond its basic applications. It plays a crucial role in several areas of advanced mathematics:
-
Modular Arithmetic: The GCF is fundamental in understanding modular arithmetic, which deals with remainders after division.
-
Number Theory: GCFs are essential in various number theory theorems and proofs, including the Euclidean algorithm itself.
-
Abstract Algebra: The concept of GCF extends to more abstract algebraic structures.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between GCF and LCM?
A: The GCF (Greatest Common Factor) is the largest number that divides both numbers, while the LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers.
-
Q: Can the GCF of two numbers be one of the numbers itself?
A: Yes, if one number is a multiple of the other, the GCF will be the smaller number. For instance, the GCF of 18 and 36 is 18.
-
Q: Is there a limit to the number of methods to find the GCF?
A: While the methods discussed are the most common and efficient, there are other less frequently used methods, especially for specific types of numbers.
Conclusion
Finding the greatest common factor of two numbers is a cornerstone of elementary number theory and has widespread practical applications. We've explored three key methods – prime factorization, listing factors, and the Euclidean algorithm – each offering a different approach to solving this fundamental mathematical problem. Understanding GCFs not only helps in simplifying fractions and solving ratio problems but also provides a foundation for more advanced mathematical concepts. Mastering these methods empowers you to tackle various mathematical challenges with greater confidence and efficiency. Remember to choose the method that best suits the numbers involved and your comfort level, always aiming for clarity and precision in your calculations.
Latest Posts
Latest Posts
-
What Is 25 Divisible By
Sep 09, 2025
-
Anisotropic To Isotropic Mri Function
Sep 09, 2025
-
Difference Between Conductor And Insulator
Sep 09, 2025
-
18 09 Is 26 8 Of What
Sep 09, 2025
-
Where To Buy Iron Metal
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 54 And 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.