How Many 1/4 In 3
salachar
Sep 03, 2025 · 6 min read
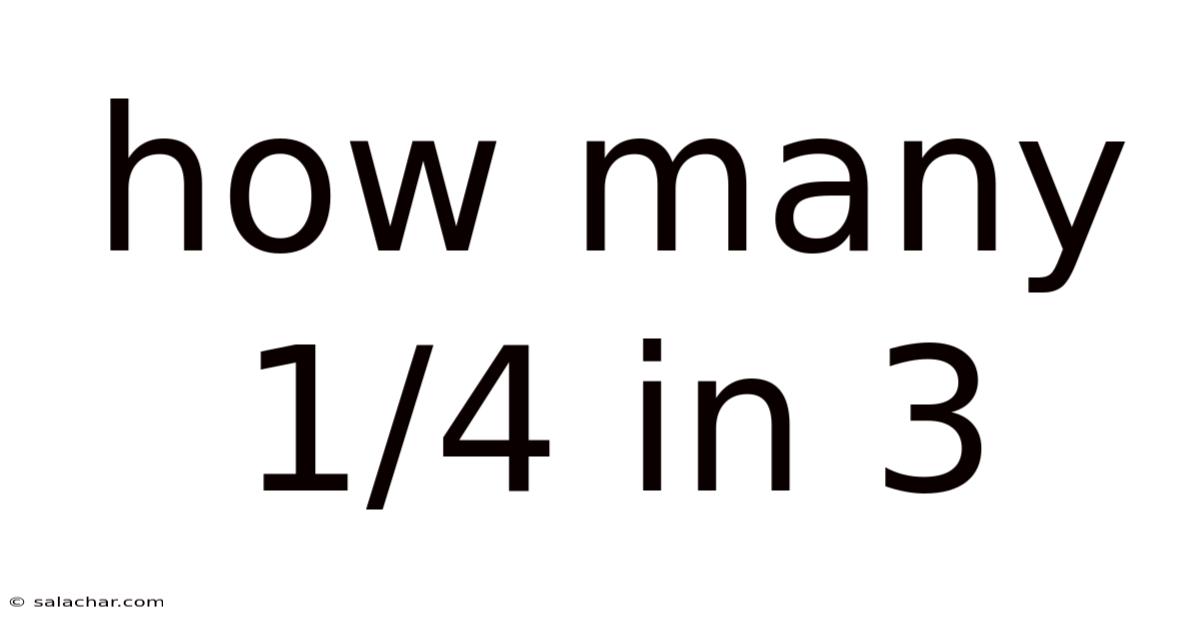
Table of Contents
How Many 1/4s are in 3? A Deep Dive into Fractions and Division
This seemingly simple question, "How many 1/4s are in 3?", opens a door to a deeper understanding of fractions, division, and the fundamental principles of mathematics. While the answer might seem immediately obvious to some, exploring the different ways to solve this problem reveals valuable insights into mathematical concepts and problem-solving strategies applicable to more complex scenarios. This article will not only provide the answer but also delve into the reasoning behind it, offering multiple approaches and explanations suitable for various learning levels. We'll cover everything from basic arithmetic to more advanced methods, ensuring a comprehensive understanding of the topic.
Understanding the Question
At its core, the question "How many 1/4s are in 3?" asks us to determine how many times the fraction 1/4 fits into the whole number 3. This is a division problem in disguise. We are essentially dividing 3 by 1/4. Understanding this fundamental relationship is crucial to solving the problem effectively.
Method 1: Using Visual Representation
A powerful way to visualize this problem is to use a simple diagram. Imagine three whole circles, each representing the number 1. Now, divide each circle into four equal quarters. Each quarter represents the fraction 1/4. By counting the total number of quarters across all three circles, we can directly see how many 1/4s are in 3.
- Step 1: Draw three circles.
- Step 2: Divide each circle into four equal parts (quarters).
- Step 3: Count the total number of quarters.
You'll find that there are 12 quarters in total. Therefore, there are 12 1/4s in 3. This visual method provides an intuitive understanding of the concept, especially for those who are new to fractions.
Method 2: Converting to an Improper Fraction
Another effective approach involves converting the whole number 3 into an improper fraction with a denominator of 4. This allows for direct comparison and division.
- Step 1: Express 3 as a fraction with a denominator of 4. To do this, we multiply 3 by 4/4 (which is equivalent to 1), giving us 12/4.
- Step 2: Now we have the fraction 12/4. This represents 3 as a fraction.
- Step 3: Divide 12/4 by 1/4. Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 1/4 is 4/1 (or simply 4). So, we have (12/4) * (4/1) = 12.
This confirms that there are 12 1/4s in 3. This method emphasizes the manipulation of fractions and demonstrates the relationship between whole numbers and their fractional equivalents.
Method 3: Using the Division Algorithm
This method uses the standard division algorithm, treating the problem as 3 ÷ (1/4). Remember that dividing by a fraction involves multiplying by its reciprocal.
- Step 1: Rewrite the problem as 3 ÷ (1/4).
- Step 2: Multiply 3 by the reciprocal of 1/4, which is 4/1 (or 4).
- Step 3: The calculation becomes 3 * 4 = 12.
Therefore, there are 12 1/4s in 3. This approach reinforces the connection between division and multiplication with fractions, a crucial concept in mathematics.
Method 4: Applying the Concept of Reciprocal
The reciprocal of a number is simply 1 divided by that number. Understanding reciprocals can greatly simplify fraction division problems. The reciprocal of 1/4 is 4. This means that there are 4 quarters in one whole. Since we have 3 wholes, we multiply 4 (quarters per whole) by 3 (number of wholes) to get 12. This highlights the efficiency of using reciprocals in fractional calculations.
Extending the Concept: Solving Similar Problems
The principles discussed above can be applied to various problems involving fractions and division. For example, let's consider "How many 1/8s are in 2?"
Following the methods described:
- Visual: Divide two circles into eight equal parts each. You will have 16 parts in total.
- Improper Fraction: 2 can be written as 16/8. (16/8) ÷ (1/8) = 16.
- Division Algorithm: 2 ÷ (1/8) = 2 * 8 = 16.
- Reciprocal: There are 8 eighths in one whole, so in two wholes there are 8 * 2 = 16 eighths.
This demonstrates the versatility of these methods in tackling different fraction-division problems.
The Importance of Understanding Fractions
The seemingly simple problem of determining how many 1/4s are in 3 provides a valuable opportunity to reinforce fundamental concepts related to fractions. A strong grasp of fractions is essential for success in higher-level mathematics, including algebra, calculus, and more. Understanding fractions is not merely about manipulating numbers; it's about developing a deep understanding of ratios, proportions, and the relationship between parts and wholes. This understanding is transferable to various real-world applications, from cooking and construction to finance and engineering.
Frequently Asked Questions (FAQs)
- Q: What if the number isn't a whole number?
A: The same principles apply. For example, to find how many 1/4s are in 2.5, you can convert 2.5 to the improper fraction 10/4. Then, (10/4) ÷ (1/4) = 10. Or, you can use the division algorithm: 2.5 ÷ 0.25 = 10.
- Q: Can I use a calculator to solve this?
A: Yes, a calculator can certainly be used. Simply input 3 ÷ (1/4) or 3 ÷ 0.25. The result will be 12. However, it's important to understand the underlying mathematical concepts to solve similar problems without relying solely on a calculator.
- Q: Why is understanding reciprocals important?
A: Reciprocals simplify division involving fractions. Instead of dividing by a fraction, you multiply by its reciprocal, which is often easier to compute. This is a fundamental concept in algebra and beyond.
- Q: Are there other ways to solve this problem?
A: While the methods described above are the most common and straightforward, more advanced mathematical techniques could also be used, but these are generally unnecessary for this specific problem.
Conclusion
The question, "How many 1/4s are in 3?", while seemingly simple, serves as an excellent gateway to understanding fundamental mathematical concepts. Through visual representation, fraction conversion, the division algorithm, and the application of reciprocals, we've explored multiple approaches to solving this problem. Mastering these methods not only provides the answer (12) but also builds a strong foundation for tackling more complex mathematical challenges. The key takeaway is that understanding the underlying principles is far more important than simply obtaining the numerical answer. The ability to analyze, interpret, and solve fractional problems is a crucial skill that transcends the classroom and finds application in numerous aspects of daily life. Remember, practice is key to mastering these concepts. The more you work with fractions and division, the more comfortable and confident you will become in solving similar problems.
Latest Posts
Latest Posts
-
Favourite Teachers My Favorite Teacher
Sep 05, 2025
-
Lewis Dot Symbol For Carbon
Sep 05, 2025
-
Refraction And Diffraction Of Light
Sep 05, 2025
-
Interesting Facts Related To Chemistry
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/4 In 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.