Integral Of Sin 2 Ax
salachar
Sep 16, 2025 · 5 min read
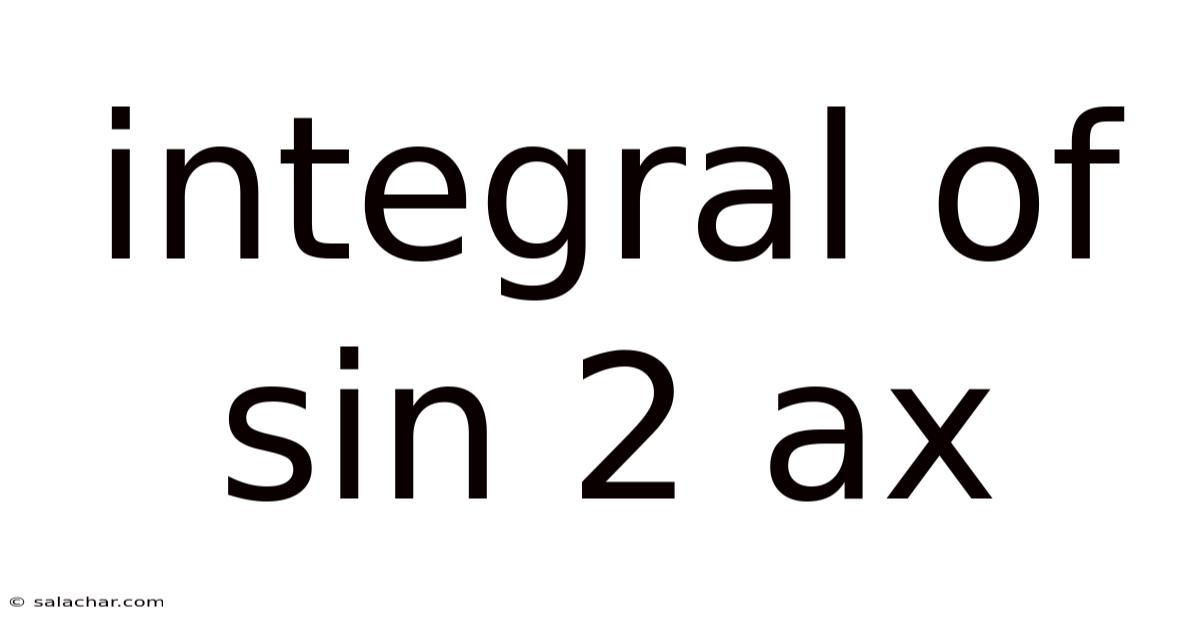
Table of Contents
Decoding the Integral of sin(2ax): A Comprehensive Guide
The integral of sin(2ax) is a fundamental concept in calculus, appearing frequently in various applications from physics and engineering to signal processing and statistics. Understanding how to solve this integral and its implications is crucial for anyone studying calculus or related fields. This article will provide a comprehensive guide, walking you through the process step-by-step, explaining the underlying principles, and exploring some real-world applications. We'll cover the solution, explore variations, delve into the scientific rationale, answer frequently asked questions, and conclude with practical advice.
Understanding the Problem: ∫sin(2ax) dx
Our goal is to find the indefinite integral of the trigonometric function sin(2ax) with respect to x. This means we are looking for a function whose derivative is sin(2ax). The presence of the constant 'a' adds a slight complexity, but the core technique remains the same.
Step-by-Step Solution: Integration Using u-Substitution
The most straightforward approach to solving this integral is using u-substitution, a powerful technique in integration.
1. Define the Substitution:
Let's define a new variable, u, as:
u = 2ax
2. Find the Differential:
Now, we need to find the differential, du, which is the derivative of u with respect to x, multiplied by dx:
du = 2a dx
3. Solve for dx:
Rearrange the equation above to solve for dx:
dx = du / (2a)
4. Substitute into the Original Integral:
Substitute u and dx into the original integral:
∫sin(2ax) dx = ∫sin(u) (du / (2a))
5. Simplify and Integrate:
The integral simplifies to:
(1 / (2a)) ∫sin(u) du
Now, we can easily integrate sin(u) with respect to u. The integral of sin(u) is -cos(u). Therefore:
(1 / (2a)) ∫sin(u) du = (1 / (2a)) (-cos(u)) + C
6. Substitute Back:
Finally, substitute back the original expression for u:
(1 / (2a)) (-cos(2ax)) + C = -cos(2ax) / (2a) + C
Where C is the constant of integration. This constant is crucial because the derivative of a constant is zero, meaning many functions can have the same derivative.
Therefore, the indefinite integral of sin(2ax) is -cos(2ax) / (2a) + C.
The Scientific Rationale: A Deeper Dive into the Process
The u-substitution method we used is based on the chain rule of differentiation. The chain rule states that the derivative of a composite function is the derivative of the outer function (with the inside function left alone) times the derivative of the inside function. Integration, being the reverse process of differentiation, employs u-substitution to effectively "undo" the chain rule. By carefully choosing our substitution (u), we simplify the integral into a more manageable form. In this case, we chose u = 2ax because it simplifies the argument of the sine function, allowing us to integrate a simpler trigonometric expression.
Variations and Extensions
The basic integral we've solved forms the basis for solving many more complex integrals. Let's consider a few variations:
-
Definite Integral: If we have limits of integration (e.g., ∫sin(2ax) dx from 0 to π), we evaluate the antiderivative at the upper and lower limits and subtract the results.
-
Integral with a Constant Multiplier: If the integral were ∫k sin(2ax) dx, where k is a constant, the solution would simply be -k cos(2ax) / (2a) + C. The constant k would simply carry through the integration process.
-
Integrals Involving Other Trigonometric Functions: The integral of sin(2ax) is frequently encountered in problems involving other trigonometric functions, often requiring the use of trigonometric identities to simplify the expression before integrating.
Frequently Asked Questions (FAQ)
Q1: Why is the constant of integration (C) important?
A: The constant of integration is crucial because the derivative of any constant is zero. Therefore, infinitely many functions can have the same derivative. The constant of integration accounts for this ambiguity and ensures that the general solution includes all possible antiderivatives.
Q2: What if 'a' is zero?
A: If a is zero, the integral becomes ∫sin(0) dx = ∫0 dx = C. The integral simplifies to a constant.
Q3: Can this integral be solved using other methods?
A: While u-substitution is the most efficient method, other techniques like integration by parts could be used, but they would be unnecessarily complicated for this particular integral.
Q4: What are some real-world applications of this integral?
A: This integral finds applications in many areas including:
- Physics: Modeling oscillatory motion (like simple harmonic motion) and wave phenomena.
- Engineering: Analyzing circuits with sinusoidal signals.
- Signal Processing: Analyzing and manipulating periodic signals.
- Probability and Statistics: In the context of Fourier analysis and probability density functions.
Conclusion: Mastering the Integral of sin(2ax)
The integral of sin(2ax) is a fundamental concept with wide-ranging applications. By understanding the u-substitution method and the underlying principles, you can confidently solve this integral and numerous variations. Remember to always include the constant of integration and to carefully check your work. Mastering this integral will significantly enhance your understanding of calculus and its practical applications in various scientific and engineering fields. With practice and a solid grasp of the fundamentals, you will find integrating trigonometric functions to be a straightforward and rewarding process. Remember, understanding the 'why' behind the mathematical processes is just as important as knowing the 'how'. This approach allows for a deeper understanding and broader application of this vital calculus skill.
Latest Posts
Latest Posts
-
Essay On Nature And Nurture
Sep 16, 2025
-
Equilibrium Solutions Of Differential Equations
Sep 16, 2025
-
Witch Vs Warlock Vs Wizard
Sep 16, 2025
-
Is Pollen Haploid Or Diploid
Sep 16, 2025
-
How Does A Spring Work
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Integral Of Sin 2 Ax . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.