Is 2/3 Bigger Than 3/4
salachar
Sep 06, 2025 · 6 min read
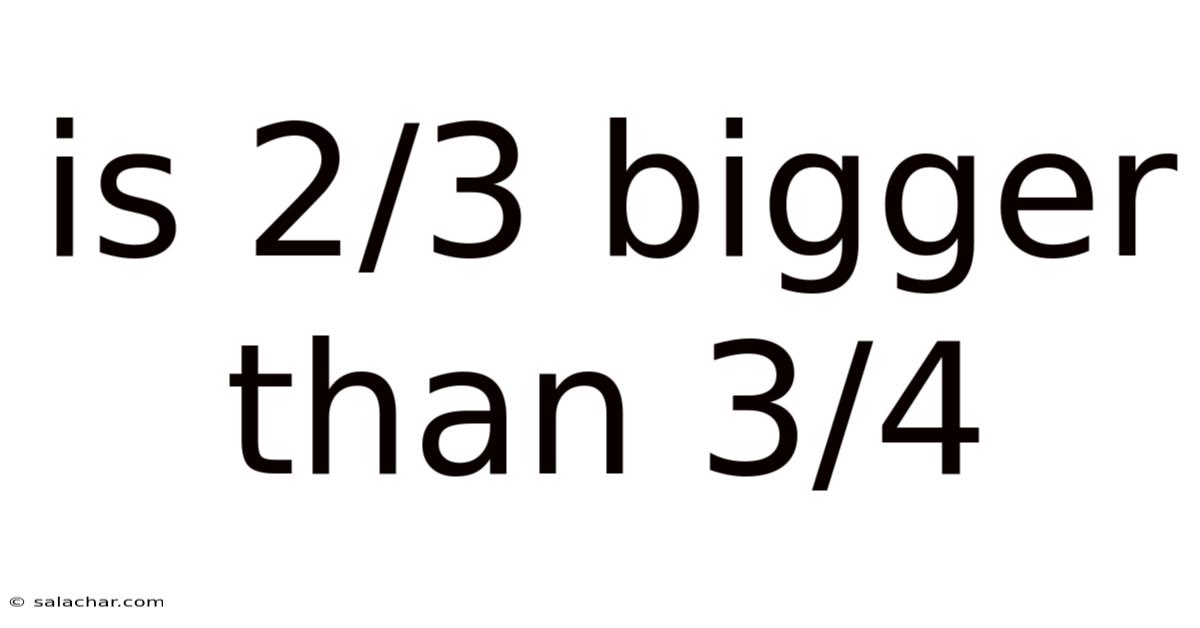
Table of Contents
Is 2/3 Bigger Than 3/4? Unraveling Fractions and Comparative Reasoning
Understanding fractions is a cornerstone of mathematical literacy. This article delves into the seemingly simple question, "Is 2/3 bigger than 3/4?", providing a comprehensive explanation suitable for learners of all levels. We'll explore different methods for comparing fractions, delve into the underlying mathematical concepts, and address common misconceptions. By the end, you'll not only know the answer but also possess a robust understanding of fractional comparison.
Introduction: Understanding Fractions
Before jumping into the comparison, let's establish a firm understanding of what fractions represent. A fraction, like 2/3 or 3/4, represents a part of a whole. The number on top (the numerator) indicates the number of parts we have, while the number on the bottom (the denominator) indicates the total number of equal parts the whole is divided into.
Imagine a pizza cut into three equal slices. 2/3 represents having two of those three slices. Similarly, if a pizza is cut into four equal slices, 3/4 represents having three of those four slices.
The question, "Is 2/3 bigger than 3/4?", essentially asks which portion of a pizza is larger: two out of three slices or three out of four slices. Intuitively, this might not be immediately obvious, highlighting the need for a systematic approach to fraction comparison.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once they share a denominator, we can directly compare their numerators.
To find a common denominator for 2/3 and 3/4, we look for the least common multiple (LCM) of 3 and 4. The LCM is the smallest number that is a multiple of both 3 and 4. In this case, the LCM is 12.
Now, we convert each fraction to have a denominator of 12:
-
2/3: To change the denominator from 3 to 12, we multiply both the numerator and the denominator by 4: (2 x 4) / (3 x 4) = 8/12
-
3/4: To change the denominator from 4 to 12, we multiply both the numerator and the denominator by 3: (3 x 3) / (4 x 3) = 9/12
Now the comparison is simple: 8/12 versus 9/12. Since 8 is less than 9, we conclude that 8/12 (or 2/3) is smaller than 9/12 (or 3/4).
Method 2: Converting to Decimals
Another effective method is converting the fractions to decimals. This involves dividing the numerator by the denominator for each fraction.
-
2/3: 2 ÷ 3 ≈ 0.6667
-
3/4: 3 ÷ 4 = 0.75
Comparing the decimal equivalents, we see that 0.6667 is less than 0.75. Therefore, 2/3 is smaller than 3/4. This method provides a clear numerical comparison, especially useful when dealing with more complex fractions or when visualization is less intuitive.
Method 3: Visual Representation
While less precise for complex fractions, visual representation can be incredibly helpful for understanding the concept. Imagine two identical circles.
Divide the first circle into three equal parts and shade two of them (representing 2/3). Divide the second circle into four equal parts and shade three of them (representing 3/4). By visually comparing the shaded areas, it becomes apparent that the shaded area in the second circle (3/4) is larger than the shaded area in the first circle (2/3). This visual approach strengthens intuitive understanding.
Method 4: Cross-Multiplication
A more advanced, yet efficient method is cross-multiplication. This technique directly compares the fractions without finding a common denominator.
Cross-multiply the fractions as follows:
(2 x 4) and (3 x 3)
This results in 8 and 9. Since 8 < 9, we conclude that 2/3 < 3/4.
The rule is: if (numerator of first fraction x denominator of second fraction) < (numerator of second fraction x denominator of first fraction), then the first fraction is smaller. Conversely, if it's greater, then the first fraction is larger.
Addressing Common Misconceptions
A common misconception is that simply comparing numerators or denominators will determine which fraction is larger. This is incorrect. Consider 1/2 and 1/10. Although 10 > 2, 1/2 is actually larger than 1/10 because half of something is more than one-tenth of it. Always use a valid comparison method as outlined above.
The Importance of Understanding Fraction Comparison
The ability to compare fractions accurately is fundamental in various aspects of mathematics and beyond. From baking and cooking (measuring ingredients) to construction (measuring materials) and data analysis (interpreting proportions), understanding fraction comparison is crucial for everyday life and professional contexts. Mastering this skill builds a strong foundation for further mathematical exploration.
Frequently Asked Questions (FAQ)
-
Q: Can I always use the common denominator method? A: Yes, the common denominator method always works, although it can be more time-consuming for fractions with large denominators. Cross-multiplication offers a faster alternative in such cases.
-
Q: Which method is best for visual learners? A: Visual representation is excellent for building intuitive understanding. Drawing diagrams or using physical objects helps to make the comparison more concrete.
-
Q: How do I compare fractions with different signs (positive and negative)? A: When comparing fractions with different signs, a positive fraction is always greater than a negative fraction. For instance, 1/2 > -3/4. If both fractions are negative, the fraction with the smaller absolute value (the value without the negative sign) is larger. For example, -1/2 > -3/4.
-
Q: What if the fractions have a common numerator instead of a common denominator? A: If fractions share the same numerator, the fraction with the smaller denominator is the larger fraction. For example, 3/5 > 3/10 because fifths are larger than tenths.
Conclusion: Mastering Fraction Comparison
Determining whether 2/3 is bigger than 3/4, initially a seemingly simple question, has led us on a journey to explore different techniques for comparing fractions. We've discovered that 2/3 is smaller than 3/4, confirmed through multiple methods: finding a common denominator, converting to decimals, visual representation, and cross-multiplication. The crucial takeaway isn't just the answer itself but the understanding of the underlying mathematical principles and the ability to apply various methods effectively. This knowledge empowers you to confidently tackle more complex fractional comparisons in the future and appreciate the versatile nature of fractions in various real-world applications. Remember to practice regularly to solidify your understanding and build your mathematical confidence.
Latest Posts
Latest Posts
-
Is Force A Vector Quantity
Sep 07, 2025
-
242 Metric Tons To Pounds
Sep 07, 2025
-
What Fahrenheit Is 37 Celsius
Sep 07, 2025
-
Blood Is Heterogeneous Or Homogeneous
Sep 07, 2025
-
What Is 5 Of 2800
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Is 2/3 Bigger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.