Lcm Of 3 4 6
salachar
Sep 09, 2025 · 6 min read
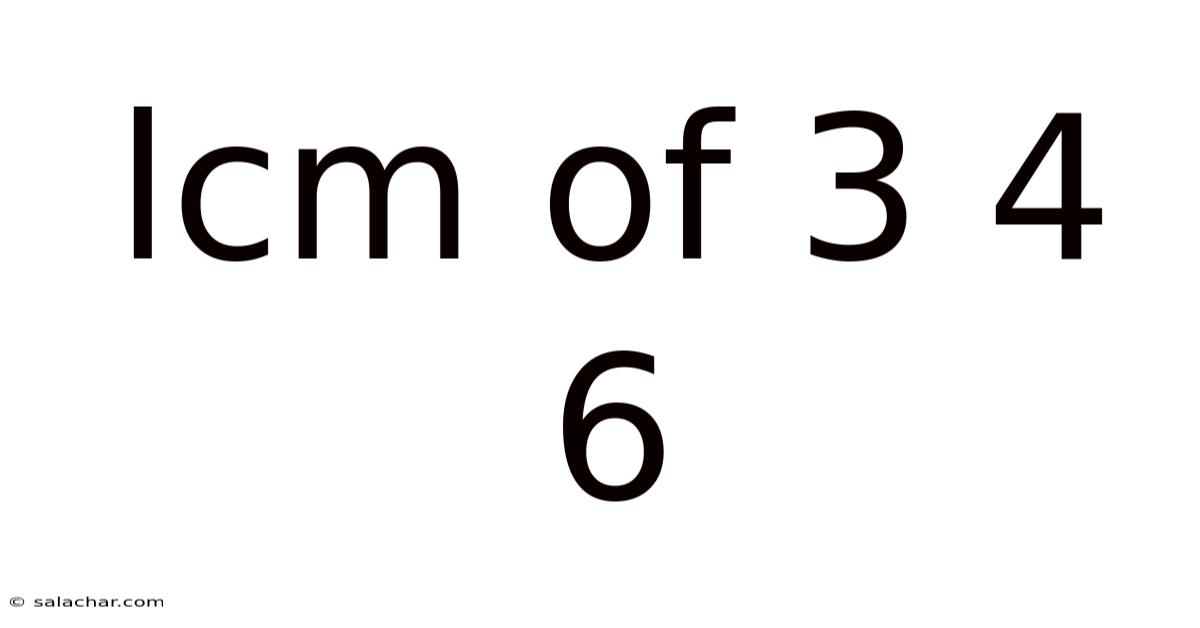
Table of Contents
Finding the LCM of 3, 4, and 6: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of numbers might seem like a simple arithmetic task, but understanding the underlying concepts unlocks a deeper appreciation for number theory and its applications in various fields. This article will not only guide you through calculating the LCM of 3, 4, and 6 but also delve into the theoretical foundation, different methods of calculation, and real-world applications of LCM. We'll explore the concept in detail, making it accessible to everyone, regardless of their mathematical background.
Introduction: What is a Least Common Multiple?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding LCM is crucial in various mathematical operations, including simplifying fractions, solving problems involving cycles and periodic events, and even in areas like music theory and computer programming.
Let's focus on our example: finding the LCM of 3, 4, and 6. This seemingly straightforward problem offers a great opportunity to illustrate different approaches to finding the LCM and to solidify the conceptual understanding behind the calculation.
Method 1: Listing Multiples
One of the simplest methods, especially for smaller numbers, is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
By examining the lists, we can see that the smallest number present in all three lists is 12. Therefore, the LCM of 3, 4, and 6 is 12. This method is intuitive but can become time-consuming and impractical for larger numbers or a greater number of integers.
Method 2: Prime Factorization
This method is more efficient and works for any set of integers. It involves breaking down each number into its prime factors. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
-
Find the prime factorization of each number:
- 3 = 3
- 4 = 2 x 2 = 2²
- 6 = 2 x 3
-
Identify the highest power of each prime factor present:
- The prime factors are 2 and 3.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3¹ = 3.
-
Multiply the highest powers together:
- LCM(3, 4, 6) = 2² x 3 = 4 x 3 = 12
This method is more systematic and less prone to errors than simply listing multiples, particularly when dealing with larger numbers. It provides a clear and concise approach to finding the LCM, highlighting the fundamental role of prime factorization in number theory.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are intimately related. The GCD is the largest number that divides all the given numbers without leaving a remainder. We can utilize the following formula:
LCM(a, b, c) = (|a x b x c|) / GCD(a, b, c)
However, this formula is most easily applied when dealing with only two numbers. For three or more numbers, it's more efficient to use a stepwise approach. First, find the LCM of two numbers, and then find the LCM of that result and the next number, and so on. Let's apply this to our example:
-
Find the LCM of 3 and 4:
- Multiples of 3: 3, 6, 9, 12...
- Multiples of 4: 4, 8, 12...
- LCM(3, 4) = 12
-
Find the LCM of 12 and 6:
- Multiples of 12: 12, 24, 36...
- Multiples of 6: 6, 12, 18, 24...
- LCM(12, 6) = 12
Therefore, the LCM of 3, 4, and 6 is 12. This method showcases the interconnectedness of LCM and GCD, reinforcing the underlying mathematical structure. While it might appear more complex initially, this approach becomes particularly useful when dealing with larger numbers and more complex scenarios.
A Deeper Look: The Mathematical Underpinnings
The concept of LCM is deeply rooted in number theory. Understanding prime factorization is key. Every integer greater than 1 can be expressed uniquely as a product of prime numbers. This fundamental theorem of arithmetic forms the bedrock for finding LCM. The method using prime factorization elegantly leverages this theorem. By expressing each number as a product of its prime factors, we can identify the common and unique factors, leading to the efficient calculation of the LCM.
Furthermore, the relationship between LCM and GCD demonstrates a fundamental duality in number theory. The product of the LCM and GCD of two numbers is equal to the product of the two numbers themselves. This property extends to multiple numbers, albeit with a more complex application.
Real-World Applications of LCM
The seemingly abstract concept of LCM finds practical applications in various aspects of life:
-
Scheduling: Imagine you have three machines that complete a cycle every 3, 4, and 6 hours respectively. The LCM (12) helps determine when all machines will complete a cycle simultaneously. This is crucial for scheduling maintenance or coordinating production lines.
-
Fraction Arithmetic: Finding the LCM of the denominators is essential when adding or subtracting fractions. This allows us to convert the fractions to a common denominator, simplifying the calculation.
-
Music Theory: Musical rhythms and time signatures often involve fractions. Understanding LCM helps musicians understand and harmonize different rhythmic patterns.
-
Computer Science: In computer programming, LCM is utilized in tasks involving cyclical processes, timing events, or resource allocation.
-
Construction & Engineering: LCM can assist in determining the optimal time for coordinating different phases of a project that have varying completion times.
Frequently Asked Questions (FAQ)
-
What if the numbers have no common factors? If the numbers are coprime (i.e., their GCD is 1), their LCM is simply the product of the numbers. For example, LCM(5, 7) = 35.
-
Can I use a calculator to find the LCM? Yes, many scientific calculators and online tools have built-in functions to calculate LCM. However, understanding the underlying methods is crucial for applying the concept in different contexts and solving more complex problems.
-
How does LCM differ from GCD? The LCM is the smallest common multiple, while the GCD is the largest common divisor. They are inversely related; a larger GCD implies a smaller LCM and vice-versa.
-
What happens if one of the numbers is zero? The LCM of any number and zero is undefined. Zero has infinitely many multiples, making it impossible to define the smallest common multiple.
Conclusion: Mastering the LCM
Finding the LCM of 3, 4, and 6, while seemingly straightforward, provides a gateway to understanding a powerful concept in number theory. Mastering LCM extends beyond simple calculations; it involves grasping the underlying principles of prime factorization, the relationship with GCD, and the versatility of its applications. By understanding these concepts, we can effectively solve a wide array of problems across various disciplines, making the seemingly simple calculation of LCM a valuable asset in our mathematical toolkit. This understanding enhances not just our mathematical skills, but also our problem-solving abilities in diverse real-world situations. Remember, the power of mathematics lies not only in the answers but in the understanding of the process that leads us to those answers.
Latest Posts
Latest Posts
-
Distance From Mars To Jupiter
Sep 09, 2025
-
Face Centered Cubic Edge Length
Sep 09, 2025
-
What Is 4 Of 600
Sep 09, 2025
-
The New Deal 3 Rs
Sep 09, 2025
-
Plaster Of Paris Chemical Formula
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 4 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.