Lcm Of 3 6 9
salachar
Sep 12, 2025 · 6 min read
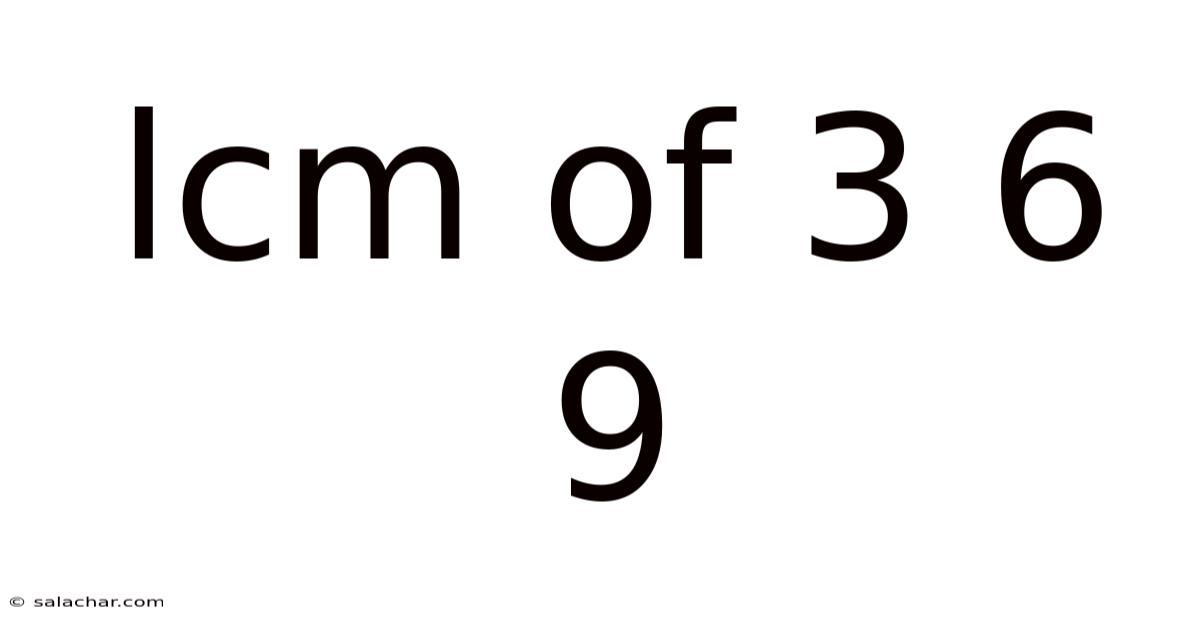
Table of Contents
Finding the LCM of 3, 6, and 9: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of 3, 6, and 9 might seem like a simple task, especially for those familiar with basic arithmetic. However, understanding the underlying principles and exploring different methods for calculating LCMs offers a valuable insight into number theory and its practical applications. This comprehensive guide will not only show you how to find the LCM of 3, 6, and 9 but will also delve deeper into the concept of LCMs, exploring various calculation methods and their applications in real-world scenarios. We'll cover everything from prime factorization to the use of the greatest common divisor (GCD), ensuring you gain a thorough understanding of this fundamental mathematical concept.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 3, 6, and 9, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21...
The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method, particularly for smaller numbers like 3, 6, and 9, is to list the multiples of each number until a common multiple is found.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 9: 9, 18, 27, 36, 45...
Observing the lists, we can see that the smallest number appearing in all three lists is 18. Therefore, the LCM of 3, 6, and 9 is 18. This method is effective for small numbers, but becomes cumbersome and inefficient when dealing with larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept of LCMs. It involves breaking down each number into its prime factors. Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 3, 6, and 9:
- 3: 3 (3 is a prime number)
- 6: 2 x 3
- 9: 3 x 3 = 3²
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ (from 6).
- The highest power of 3 is 3² (from 9).
Now, multiply these highest powers together: 2¹ x 3² = 2 x 9 = 18. Therefore, the LCM of 3, 6, and 9 is 18. This method is generally preferred for larger numbers as it provides a systematic and efficient approach.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD of two or more integers is the largest positive integer that divides all the integers without leaving a remainder. There's a formula connecting the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, but the calculation becomes more complex. Let's first find the GCD of 3, 6, and 9. We can use the Euclidean algorithm for this:
- GCD(3, 6) = 3
- GCD(3, 9) = 3
- Therefore, GCD(3, 6, 9) = 3
While this formula directly relates LCM and GCD, applying it to more than two numbers requires a more iterative approach, which makes the prime factorization method often more straightforward for finding the LCM of multiple numbers. For this particular example, while we can calculate the GCD, using it to directly compute the LCM is less efficient than the prime factorization method.
Applications of LCM in Real-World Scenarios
Understanding LCMs extends beyond theoretical mathematics; it has practical applications in various real-world scenarios:
-
Scheduling: Imagine you have two events that occur at regular intervals. One event occurs every 3 days, and another every 6 days. To find out when both events will occur simultaneously, you need to find the LCM of 3 and 6, which is 6. Both events will occur together every 6 days. This principle extends to more complex scheduling problems involving multiple events with different intervals.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. The LCM becomes the common denominator, simplifying the addition or subtraction process.
-
Modular Arithmetic: LCM plays a significant role in modular arithmetic, which is used in cryptography and other areas of computer science.
-
Construction and Engineering: In construction projects, LCM is used to determine the optimal timing for various tasks, ensuring efficient resource allocation and project completion.
-
Music Theory: LCM is used in music theory to determine the least common multiple of note durations, allowing the creation of rhythmically complex musical pieces.
Frequently Asked Questions (FAQ)
Q: What is the difference between LCM and GCD?
A: The LCM (Least Common Multiple) is the smallest positive integer that is a multiple of all the given integers. The GCD (Greatest Common Divisor) is the largest positive integer that divides all the given integers without leaving a remainder.
Q: Can the LCM of two numbers be greater than both numbers?
A: Yes, the LCM is always greater than or equal to the largest of the given numbers. If the numbers share a common factor greater than 1, the LCM will be larger than the greatest of the numbers.
Q: Is there a way to calculate the LCM of more than three numbers?
A: Yes, the prime factorization method works perfectly well for any number of integers. Find the prime factorization of each number and then take the highest power of each prime factor that appears in any of the factorizations. Multiply these highest powers together to find the LCM.
Q: What if one of the numbers is zero?
A: The LCM of any set of numbers that includes zero is undefined. This is because zero is a multiple of every number, so there's no smallest positive multiple that is divisible by all the numbers in the set.
Conclusion
Finding the LCM of 3, 6, and 9, while seemingly simple, provides a gateway to understanding the broader concept of least common multiples and their application across various fields. We explored three distinct methods – listing multiples, prime factorization, and utilizing the GCD – each offering a unique perspective and level of efficiency. The prime factorization method, in particular, is highly recommended for its general applicability and ease of use, especially when dealing with larger numbers. Understanding LCMs isn't just about solving mathematical problems; it's about grasping a fundamental concept with far-reaching implications in various aspects of our world. From scheduling events to simplifying fraction calculations, the principles of LCMs are deeply intertwined with our daily lives. The exploration presented here offers not only a solution but a profound understanding of this important mathematical concept.
Latest Posts
Latest Posts
-
First Law For Open System
Sep 12, 2025
-
Number Of Neutrons In O
Sep 12, 2025
-
Female Names That Mean Wolf
Sep 12, 2025
-
A Quadrilateral Is A Rhombus
Sep 12, 2025
-
The Blue Print Of Life
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 6 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.