Lcm Of 36 And 45
salachar
Sep 10, 2025 · 6 min read
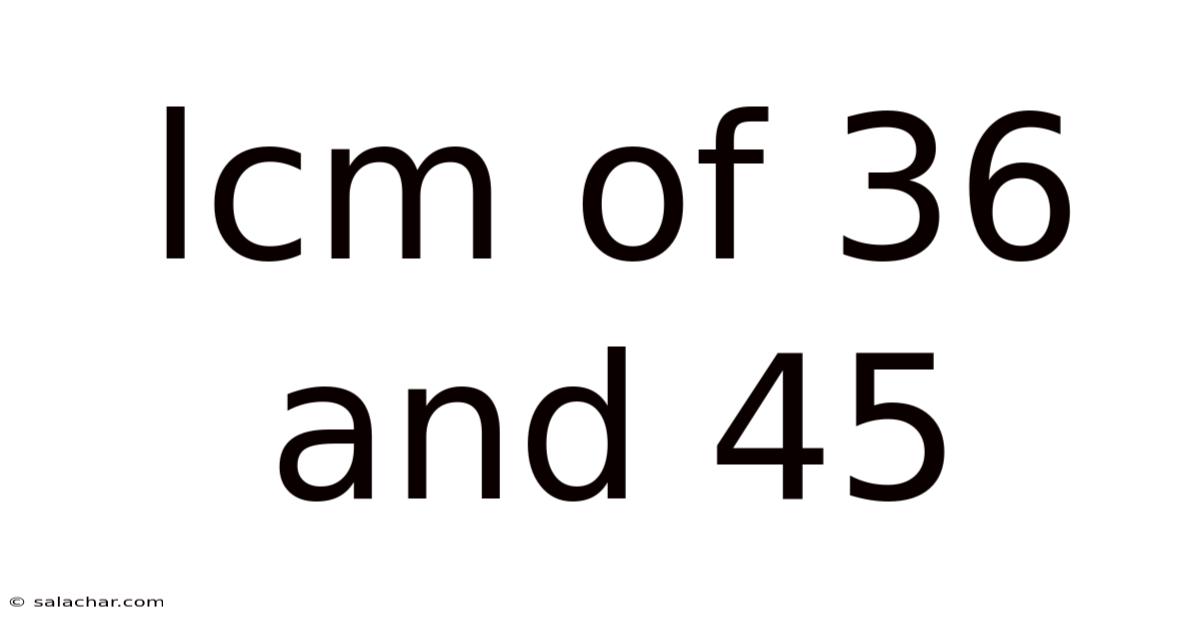
Table of Contents
Finding the LCM of 36 and 45: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers, like 36 and 45, might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating the LCM provides a valuable foundation in number theory and its applications in various fields, from scheduling tasks to understanding musical harmony. This article will explore the LCM of 36 and 45 in detail, examining various approaches and expanding upon the core mathematical principles involved.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that both (or all) of the given numbers can divide into without leaving a remainder. This concept is crucial in various applications, including:
- Scheduling: Determining when events will occur simultaneously. For example, if two buses arrive at a station every 36 minutes and 45 minutes respectively, finding the LCM helps determine when they'll both arrive at the same time.
- Fractions: Finding a common denominator when adding or subtracting fractions.
- Music: Understanding rhythmic patterns and harmonies. Different musical notes can have frequencies that are multiples of a fundamental frequency. The LCM helps in understanding the synchronization and harmony between these notes.
- Modular Arithmetic: Used extensively in cryptography and computer science.
Method 1: Listing Multiples
The most straightforward method, albeit time-consuming for larger numbers, is to list the multiples of each number until a common multiple is found.
- Multiples of 36: 36, 72, 108, 144, 180, 216, 252, 288, 324, 360, ...
- Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360, ...
Notice that 180 appears in both lists. However, a smaller common multiple, 180, is found before encountering any larger ones. Therefore, the LCM of 36 and 45 is 180. This method works well for smaller numbers but becomes impractical for larger ones.
Method 2: Prime Factorization
This method is more efficient, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 36: 36 = 2² x 3²
- Prime factorization of 45: 45 = 3² x 5
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2² = 4
- Highest power of 3: 3² = 9
- Highest power of 5: 5¹ = 5
Now, multiply these highest powers together:
LCM(36, 45) = 2² x 3² x 5 = 4 x 9 x 5 = 180
This method is significantly more efficient than listing multiples, especially for larger numbers. It provides a systematic approach that avoids the trial-and-error involved in listing multiples.
Method 3: Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. The relationship is expressed as:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 36 and 45 using the Euclidean algorithm:
- Divide the larger number (45) by the smaller number (36): 45 = 1 x 36 + 9
- Replace the larger number with the smaller number (36) and the smaller number with the remainder (9): 36 = 4 x 9 + 0
Since the remainder is 0, the GCD is 9.
Now, we can use the formula:
LCM(36, 45) = (36 x 45) / GCD(36, 45) = (36 x 45) / 9 = 180
This method is efficient because it uses the GCD, which can be calculated relatively quickly using the Euclidean algorithm. This approach is particularly helpful when dealing with larger numbers where prime factorization might be more time-consuming.
Explanation of the Methods: A Deeper Dive
The effectiveness of each method hinges on the mathematical principles at play:
-
Listing Multiples: This method is fundamentally based on the definition of a multiple. Every multiple of a number is obtained by multiplying it by an integer. By listing multiples, we systematically search for the smallest number that appears in both lists, thus satisfying the definition of the LCM. However, its inefficiency stems from its exhaustive nature – it requires generating a potentially large number of multiples before finding a common one.
-
Prime Factorization: This method is rooted in the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely expressed as a product of prime numbers. By breaking down the numbers into their prime factors, we identify the essential building blocks of the numbers. The LCM is then constructed by selecting the highest power of each prime factor present in the factorizations. This directly addresses the core requirement of the LCM: it must contain all the prime factors of both numbers with the highest possible powers to ensure divisibility.
-
GCD Method: This method relies on the fundamental relationship between the LCM and GCD. The Euclidean algorithm efficiently finds the GCD, leveraging the properties of division with remainders. The formula connecting LCM and GCD elegantly encapsulates the relationship between these two crucial concepts, offering a concise and efficient way to calculate the LCM once the GCD is known.
Frequently Asked Questions (FAQ)
-
What if the numbers are relatively prime? If two numbers are relatively prime (their GCD is 1), their LCM is simply their product. For instance, LCM(15, 28) = 15 x 28 = 420 because their GCD is 1.
-
Can I use this for more than two numbers? Yes, the prime factorization method can be extended to find the LCM of more than two numbers. You would find the prime factorization of each number and then select the highest power of each prime factor present among all the factorizations.
-
Why is the LCM important in real-world applications? The LCM is crucial for coordinating events with different periodicities, like scheduling tasks, designing rhythmic patterns in music, or managing processes in manufacturing that need synchronized operation.
Conclusion:
Finding the LCM of 36 and 45, while seemingly simple, reveals a wealth of mathematical concepts. We've explored three different methods: listing multiples, prime factorization, and the GCD method. Each method offers a unique perspective and level of efficiency, highlighting the versatility of number theory. Understanding the LCM is not merely an arithmetic exercise but a stepping stone to grasping deeper mathematical principles with significant applications across various disciplines. Choosing the most appropriate method depends on the context and the magnitude of the numbers involved. For smaller numbers, listing multiples is manageable, but for larger numbers, the prime factorization or GCD method is far more efficient and systematic. This comprehensive exploration aims to solidify your understanding of LCM and its importance in both theoretical and practical settings.
Latest Posts
Latest Posts
-
Characteristics Of A Great Mother
Sep 10, 2025
-
Plaster Of Paris Wall Art
Sep 10, 2025
-
Why Is Electron Affinity Negative
Sep 10, 2025
-
Waters Boiling Point In Kelvin
Sep 10, 2025
-
60 Minutes How Many Seconds
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 36 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.