Log Base 4 Of 1
salachar
Sep 08, 2025 · 6 min read
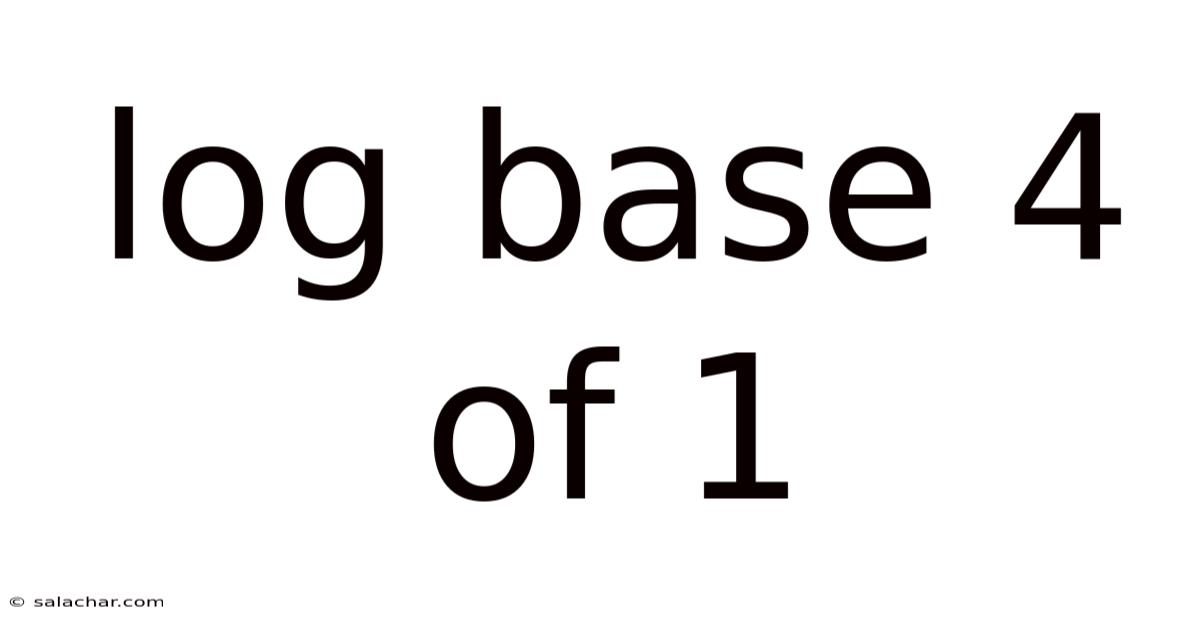
Table of Contents
Understanding Log Base 4 of 1: A Comprehensive Guide
Logarithms can seem daunting at first, but understanding their fundamental principles reveals their elegant simplicity and widespread utility in mathematics and beyond. This article delves into the specific case of log base 4 of 1, explaining not only its solution but also the underlying concepts that govern logarithmic operations. We'll cover the definition of logarithms, explore different approaches to solving this problem, discuss related properties, and even touch upon the practical applications of logarithms. By the end, you’ll have a solid grasp of this seemingly simple yet conceptually rich topic.
What are Logarithms?
Before tackling log base 4 of 1, let's establish a solid foundation. A logarithm is essentially the inverse operation of exponentiation. In simpler terms, if we have an equation like b<sup>x</sup> = y, then the logarithm is expressed as log<sub>b</sub>y = x. Here:
- b is the base of the logarithm (it's the number being raised to a power).
- y is the argument (it's the result of the exponentiation).
- x is the exponent or the logarithm itself (it's the power to which the base must be raised to obtain the argument).
Think of it like this: exponentiation asks "What is b raised to the power of x?", while the logarithm asks "To what power must b be raised to get y?".
Solving log<sub>4</sub>1: The Direct Approach
Now, let's address the question at hand: log<sub>4</sub>1. This means we're looking for the exponent (x) such that 4<sup>x</sup> = 1. We can solve this directly by considering the properties of exponents:
Any number (except 0) raised to the power of 0 equals 1. Therefore:
4<sup>0</sup> = 1
Consequently, log<sub>4</sub>1 = 0.
This is a fundamental property of logarithms: the logarithm of 1 with any valid base (a base greater than 0 and not equal to 1) is always 0.
Understanding the Logarithmic Function Graphically
Visualizing logarithmic functions can further solidify our understanding. Let's consider the graph of the function y = log<sub>4</sub>x. This is the inverse function of y = 4<sup>x</sup>. The graph of y = 4<sup>x</sup> shows exponential growth, while its inverse, y = log<sub>4</sub>x, shows logarithmic growth. Crucially, the point (1, 0) always lies on the graph of any logarithmic function where the base is positive and not equal to 1. This is because, regardless of the base, log<sub>b</sub>1 = 0, confirming our earlier calculation.
Change of Base Formula and its Relevance
While directly solving log<sub>4</sub>1 is straightforward, let's explore the change of base formula. This formula allows us to convert a logarithm from one base to another. The formula is:
log<sub>b</sub>a = log<sub>c</sub>a / log<sub>c</sub>b
Where 'a' is the argument, 'b' is the original base, and 'c' is the new base. We could use this formula to calculate log<sub>4</sub>1 using a common base like 10 or e (the natural logarithm base):
log<sub>4</sub>1 = log<sub>10</sub>1 / log<sub>10</sub>4 = 0 / log<sub>10</sub>4 = 0
or
log<sub>4</sub>1 = ln1 / ln4 = 0 / ln4 = 0
This reinforces our previous finding that log<sub>4</sub>1 = 0. The change of base formula, however, is most useful when dealing with logarithms that aren't as easily solvable directly.
Properties of Logarithms: Expanding the Understanding
Understanding the properties of logarithms is essential for manipulating and simplifying logarithmic expressions. Several key properties are relevant here:
- Product Rule: log<sub>b</sub>(xy) = log<sub>b</sub>x + log<sub>b</sub>y
- Quotient Rule: log<sub>b</sub>(x/y) = log<sub>b</sub>x - log<sub>b</sub>y
- Power Rule: log<sub>b</sub>(x<sup>p</sup>) = p * log<sub>b</sub>x
- Logarithm of 1: log<sub>b</sub>1 = 0 (as demonstrated above)
- Logarithm of the Base: log<sub>b</sub>b = 1
These properties are fundamental to solving more complex logarithmic equations and simplifying expressions. For instance, if we were presented with a more complicated equation involving log base 4, understanding these properties would be crucial for its solution.
Applications of Logarithms: Beyond the Classroom
Logarithms are not just abstract mathematical concepts; they have numerous practical applications across various fields:
- Chemistry: pH calculations (measuring acidity and alkalinity) utilize the logarithmic scale.
- Physics: Measuring sound intensity (decibels) and earthquake magnitude (Richter scale) both involve logarithmic scales.
- Computer Science: Logarithmic algorithms are widely used in computer science for efficient searching and sorting (e.g., binary search).
- Finance: Compound interest calculations often involve logarithmic functions.
- Engineering: Signal processing and data analysis frequently employ logarithmic transformations.
Frequently Asked Questions (FAQs)
Q1: Can the base of a logarithm be any number?
A1: No. The base of a logarithm must be a positive number, and it cannot be 1. This is because 1 raised to any power is always 1, making it impossible to define a unique logarithm.
Q2: What is the significance of the natural logarithm (ln)?
A2: The natural logarithm is a logarithm with base e, where e is Euler's number (approximately 2.71828). It has significant importance in calculus and many areas of science and engineering due to its relationship with exponential growth and decay processes.
Q3: How do I solve logarithmic equations that are more complex than log<sub>4</sub>1?
A3: Solving more complex logarithmic equations often involves using the properties of logarithms mentioned earlier. You might need to combine these properties to simplify the equation and then use algebraic manipulation to solve for the unknown variable. In some cases, numerical methods might be necessary.
Q4: Are there any limitations to using the change of base formula?
A4: The change of base formula is a powerful tool, but it's crucial to ensure that the new base you choose is also a valid logarithmic base (positive and not equal to 1).
Q5: Why is the logarithm of 1 always 0 regardless of the base?
A5: This stems directly from the definition of logarithms and the property that any number (except 0) raised to the power of 0 equals 1. It's a fundamental property inherent in the nature of exponential and logarithmic functions.
Conclusion: A Deeper Appreciation for Logarithms
This in-depth exploration of log base 4 of 1 has moved beyond a simple numerical answer. We've unearthed the underlying principles governing logarithmic operations, highlighted the importance of understanding logarithmic properties, and showcased the wide-ranging applications of logarithms in various fields. While seemingly straightforward, the concept of log<sub>4</sub>1 provides a crucial stepping stone to understanding the broader world of logarithms, a powerful tool with significant implications across numerous disciplines. Hopefully, this comprehensive guide has not only solved the problem but has also equipped you with a deeper and more nuanced understanding of logarithms. Remember, the key to mastering logarithms lies in practicing and applying the fundamental principles and properties we’ve explored.
Latest Posts
Latest Posts
-
What Are Man Made Elements
Sep 09, 2025
-
How Long Till October 3rd
Sep 09, 2025
-
Picture Of A Jersey Cow
Sep 09, 2025
-
Examples Of Values In Family
Sep 09, 2025
-
Where Did Wool Come From
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Log Base 4 Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.