Log Base 4 Of 4
salachar
Sep 13, 2025 · 7 min read
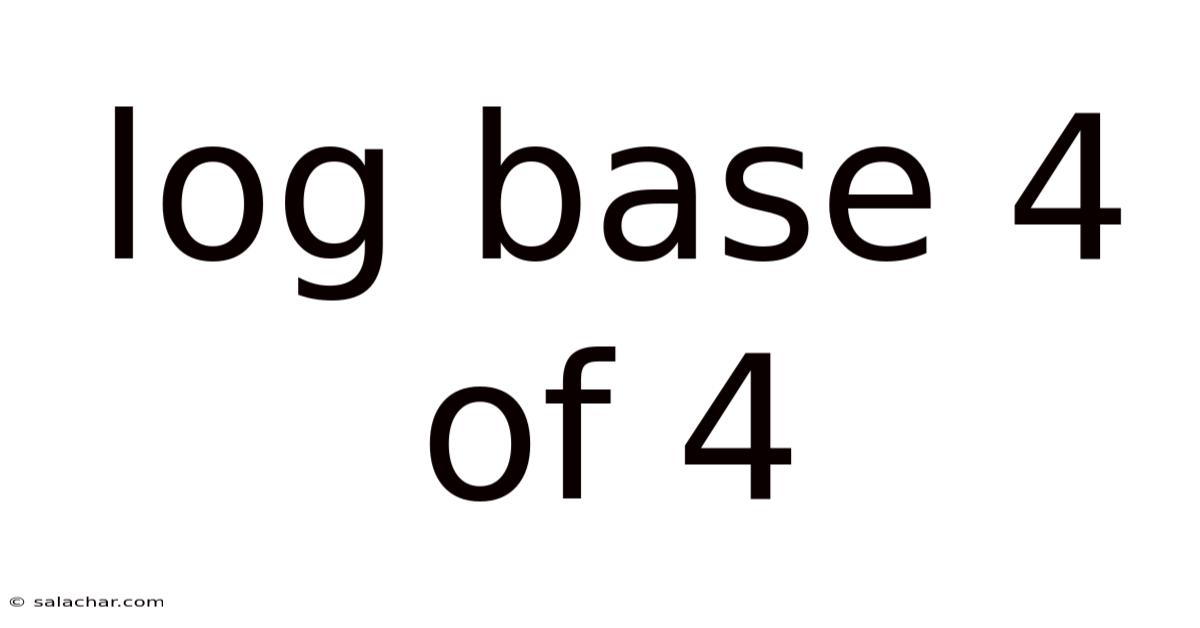
Table of Contents
Decoding the Mystery: Log₄4 and the Fundamentals of Logarithms
Logarithms, often perceived as daunting mathematical concepts, are actually powerful tools with widespread applications across various fields, from physics and engineering to finance and computer science. Understanding logarithms is crucial for grasping exponential growth and decay, solving complex equations, and interpreting data on a logarithmic scale. This article dives deep into the seemingly simple expression "log₄4," unraveling its meaning, exploring the underlying principles of logarithms, and demonstrating its relevance in a broader mathematical context. We will also address frequently asked questions to solidify your understanding.
Introduction to Logarithms: Unveiling the Inverse Relationship
Before tackling log₄4, let's establish a firm foundation in logarithmic principles. A logarithm is essentially the inverse operation of exponentiation. In simpler terms, if we have an exponential equation like b<sup>x</sup> = y, its logarithmic equivalent is log<sub>b</sub>y = x. Here:
- b represents the base of the logarithm (and the base of the exponent). It must be a positive number other than 1.
- y represents the argument or antilogarithm, the result of the exponential operation. It must also be positive.
- x represents the exponent or logarithm, the power to which the base must be raised to obtain the argument.
So, what does this mean in practical terms? If we ask "What is the logarithm base 10 of 100 (log₁₀100)?" we're essentially asking, "To what power must we raise 10 to get 100?" The answer is 2, because 10² = 100. Therefore, log₁₀100 = 2.
Understanding Log₄4: A Straightforward Case
Now, let's address the specific question: What is log₄4? Using the definition above, we're asking, "To what power must we raise 4 to obtain 4?" The answer is immediately apparent: 1. Because 4¹ = 4. Therefore, log₄4 = 1.
This seemingly simple example highlights a crucial property of logarithms: log<sub>b</sub>b = 1 for any positive base b (b ≠ 1). This property holds true because any number raised to the power of 1 equals itself.
Properties of Logarithms: Expanding the Toolkit
Understanding the properties of logarithms is critical for manipulating and simplifying logarithmic expressions. These properties are derived directly from the rules of exponents and are essential for solving more complex logarithmic equations and problems. Here are some key properties:
- Product Rule: log<sub>b</sub>(xy) = log<sub>b</sub>x + log<sub>b</sub>y. The logarithm of a product is the sum of the logarithms.
- Quotient Rule: log<sub>b</sub>(x/y) = log<sub>b</sub>x - log<sub>b</sub>y. The logarithm of a quotient is the difference of the logarithms.
- Power Rule: log<sub>b</sub>(x<sup>p</sup>) = p log<sub>b</sub>x. The logarithm of a power is the exponent times the logarithm of the base.
- Change of Base Rule: log<sub>b</sub>x = (log<sub>a</sub>x) / (log<sub>a</sub>b). This rule allows you to change the base of a logarithm from one base to another. This is particularly useful when using calculators, which typically only have base 10 or base e (natural logarithm) functions.
- Logarithm of 1: log<sub>b</sub>1 = 0 for any positive base b (b ≠ 1). This is because b<sup>0</sup> = 1.
These properties are fundamental for simplifying complex logarithmic expressions and solving logarithmic equations. Mastering them will significantly enhance your ability to work with logarithms effectively.
Logarithms in Different Bases: Exploring Common Scenarios
While base 4 is used in our example, logarithms can be expressed in various bases. The most common bases are:
- Base 10 (Common Logarithm): Often written as log x (without explicitly stating the base). This is the base used in many scientific and engineering applications.
- Base e (Natural Logarithm): Written as ln x, where e is Euler's number (approximately 2.71828). The natural logarithm is widely used in calculus and many scientific fields due to its close relationship with exponential functions and their derivatives.
- Base 2 (Binary Logarithm): Frequently employed in computer science and information theory, often used to describe the number of bits required to represent a number.
The choice of base depends heavily on the context of the problem. However, remember the change of base rule allows for conversion between different bases if needed.
Applications of Logarithms: From Science to Finance
Logarithms are not merely abstract mathematical concepts; they have real-world applications across a multitude of disciplines:
- Physics and Engineering: Logarithmic scales are used to represent phenomena with wide ranges of values, such as sound intensity (decibels), earthquake magnitude (Richter scale), and acidity (pH scale).
- Chemistry: pH calculations, which measure the acidity or alkalinity of a solution, rely heavily on logarithms.
- Finance: Logarithms are used in compound interest calculations and modeling exponential growth and decay in financial markets.
- Computer Science: Logarithmic algorithms are used in various computational tasks, such as searching and sorting, due to their efficiency. Binary logarithms are particularly relevant in analyzing algorithm complexity and data structures.
- Biology: Logarithmic scales are used to represent bacterial growth curves and population dynamics.
The versatility of logarithms makes them an indispensable tool in tackling complex problems across various scientific and technological domains.
Solving Logarithmic Equations: A Practical Application
Understanding the properties of logarithms is crucial for solving logarithmic equations. Let's consider an example:
Solve for x: log₂(x + 1) + log₂(x - 1) = 3
Using the product rule, we can simplify the left-hand side:
log₂[(x + 1)(x - 1)] = 3
This simplifies to:
log₂(x² - 1) = 3
Converting to exponential form:
x² - 1 = 2³
x² - 1 = 8
x² = 9
x = ±3
However, we must check for extraneous solutions. Since the argument of a logarithm must be positive, x + 1 > 0 and x - 1 > 0. This means x > 1. Therefore, only x = 3 is a valid solution.
This example demonstrates the importance of using logarithmic properties and carefully checking for extraneous solutions when solving logarithmic equations.
Advanced Topics in Logarithms: A Glimpse into Further Exploration
For those seeking a deeper understanding, here are some more advanced concepts related to logarithms:
- Complex Logarithms: Extending the concept of logarithms to complex numbers.
- Logarithmic Differentiation: A technique used in calculus to differentiate functions involving products, quotients, and powers.
- Taylor and Maclaurin Series for Logarithmic Functions: Representing logarithmic functions as infinite sums, useful in approximation and analysis.
- Applications in Differential Equations: Logarithms play a significant role in solving certain types of differential equations.
Exploring these advanced topics will further enhance your comprehension of the power and versatility of logarithms in mathematics and its applications.
Frequently Asked Questions (FAQ)
Q: What is the difference between log and ln?
A: log typically refers to the common logarithm (base 10), while ln denotes the natural logarithm (base e).
Q: Can the base of a logarithm be negative or zero?
A: No, the base of a logarithm must be a positive number other than 1. This is because negative bases would lead to complex numbers for certain exponents, and a base of 1 would render the logarithm undefined.
Q: What happens if the argument of a logarithm is negative?
A: The logarithm of a negative number is undefined in the real number system. However, the concept can be extended to complex numbers using complex logarithms.
Q: How can I calculate logarithms without a calculator?
A: For simple cases, you can use the definition and properties of logarithms. For more complex cases, approximation techniques or logarithmic tables can be used.
Q: Are there any limitations to using logarithms?
A: While logarithms are powerful tools, they are not always applicable. For instance, they are not defined for negative arguments (in the real number system) or for a base of 1.
Conclusion: Mastering Logarithms – A Key to Mathematical Proficiency
This comprehensive exploration of log₄4 has not only answered the specific question but has also provided a foundational understanding of logarithms and their applications. From the simple yet significant result of log₄4 = 1, we’ve expanded to cover crucial properties, various bases, real-world applications, and techniques for solving logarithmic equations. Remember, consistent practice and a solid grasp of logarithmic properties are crucial for successfully navigating the world of logarithms and leveraging their power in diverse fields. By understanding these principles, you unlock a valuable mathematical tool with far-reaching applications across numerous disciplines.
Latest Posts
Latest Posts
-
Which Fruit Has Seed Outside
Sep 13, 2025
-
Drain Flies Baking Soda Vinegar
Sep 13, 2025
-
Present Continuous And Future Continuous
Sep 13, 2025
-
Color Of Flame Calcium Chloride
Sep 13, 2025
-
Derivative Of Sinh And Cosh
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Log Base 4 Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.