Log Base 4 Of 8
salachar
Sep 10, 2025 · 5 min read
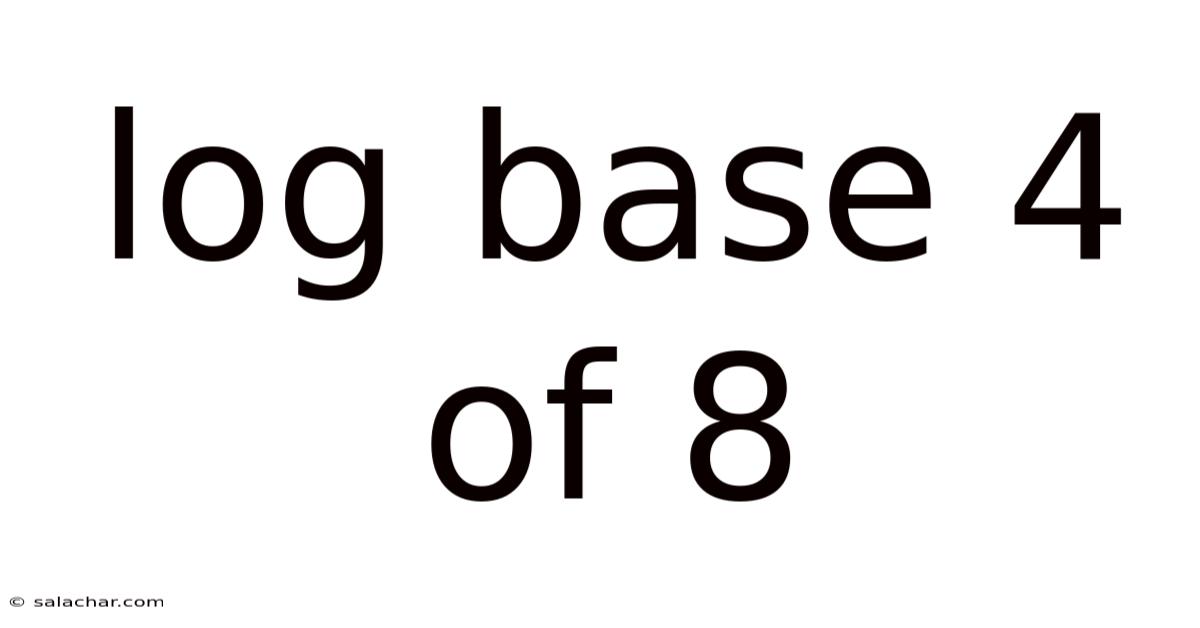
Table of Contents
Decoding the Mystery: A Deep Dive into Log₄8
Understanding logarithms might seem daunting at first, but with a clear explanation and a focus on practical application, the concept becomes significantly more accessible. This article delves into the seemingly simple, yet surprisingly revealing, logarithmic expression: log₄8. We'll unpack its meaning, explore various methods to solve it, and even discuss its broader implications within mathematics and beyond. This exploration will not only help you understand this specific logarithm but also equip you with a solid foundation for tackling more complex logarithmic problems.
What is a Logarithm? A Gentle Introduction
Before we jump into log₄8, let's establish a firm understanding of logarithms themselves. A logarithm answers the question: "To what power must we raise a base to obtain a given number?" In the general expression logₐb = x, 'a' is the base, 'b' is the argument (or number), and 'x' is the exponent. This equation is equivalent to the exponential equation aˣ = b.
In simpler terms, if we have log₂8 = 3, this means 2 raised to the power of 3 equals 8 (2³ = 8). The logarithm essentially "undoes" an exponential operation.
Understanding Log₄8: Breaking Down the Components
Now, let's focus on our specific expression: log₄8. Here:
- Base (a): 4
- Argument (b): 8
- Exponent (x): This is what we need to find.
Therefore, the question we're trying to answer is: "To what power must we raise 4 to obtain 8?"
Method 1: Using the Change of Base Formula
One of the most effective ways to solve log₄8 is by employing the change of base formula. This formula allows us to convert a logarithm with any base into a logarithm with a more convenient base, typically 10 or e (the natural logarithm base). The formula is:
logₐb = logₓb / logₓa
Where 'x' can be any base (usually 10 or e).
Let's use base 10:
log₄8 = log₁₀8 / log₁₀4
Using a calculator:
log₁₀8 ≈ 0.903 log₁₀4 ≈ 0.602
Therefore:
log₄8 ≈ 0.903 / 0.602 ≈ 1.5
This method provides a numerical approximation.
Method 2: Expressing with a Common Base
A more elegant and precise method involves expressing both the base and the argument as powers of a common base. Since both 4 and 8 are powers of 2, we can rewrite the expression as:
log₄8 = log₂²8 = log₂(2³)
Using the logarithm power rule (logₐbⁿ = n logₐb), we get:
log₂(2³) = 3 log₂2
Since log₂2 = 1 (because 2¹ = 2), the equation simplifies to:
3 * 1 = 3
This reveals that log₄8 = 1.5 (because 3/2 = 1.5). This is a precise answer, unlike the approximation from the change of base method. It showcases the power of expressing numbers in terms of their prime factorization.
Method 3: Using the Definition of Logarithms Directly
We can also solve this directly by considering the definition of a logarithm. We are looking for an exponent 'x' such that 4ˣ = 8. We can rewrite this equation using powers of 2:
(2²)ˣ = 2³
Simplifying the left side, we get:
2²ˣ = 2³
Since the bases are equal, we can equate the exponents:
2x = 3
Solving for x:
x = 3/2 = 1.5
Again, we arrive at the precise solution: log₄8 = 1.5
The Significance of the Result: What Does Log₄8 = 1.5 Tell Us?
The result, log₄8 = 1.5, tells us that raising the base 4 to the power of 1.5 (or 3/2) will result in the argument 8. We can verify this:
4^(3/2) = (2²)^(3/2) = 2^(2 * 3/2) = 2³ = 8
This demonstrates the inverse relationship between exponents and logarithms.
Logarithms in the Real World: Beyond the Classroom
Logarithms might seem like abstract mathematical concepts, but they have widespread practical applications in various fields:
- Chemistry: Calculating pH values (acidity/alkalinity) uses the logarithmic scale.
- Physics: Measuring sound intensity (decibels) and earthquake magnitudes (Richter scale) rely on logarithmic scales.
- Computer Science: Logarithmic algorithms are fundamental to efficient data structures and searching algorithms (e.g., binary search).
- Finance: Compound interest calculations often involve logarithms.
- Engineering: Analyzing signal strength and attenuation in communication systems utilizes logarithmic scales.
Understanding logarithms empowers us to interpret and analyze data across diverse scientific and engineering disciplines.
Frequently Asked Questions (FAQ)
-
Q: Can I use any base for the change of base formula? A: Yes, you can use any positive base other than 1. However, bases 10 and e are commonly used due to their availability on calculators and their mathematical properties.
-
Q: Why is expressing numbers in terms of a common base helpful? A: Expressing numbers as powers of a common base allows us to simplify logarithmic expressions and often leads to more direct and elegant solutions.
-
Q: Are there other methods to solve log₄8? A: Yes, more advanced techniques like using the properties of logarithms (e.g., product rule, quotient rule) could be employed for more complex logarithmic expressions. However, for log₄8, the methods described above are the most straightforward and efficient.
-
Q: What if the argument is not a perfect power of the base? A: In that case, using the change of base formula or numerical approximation techniques will be necessary. You won't be able to find an exact, rational solution.
Conclusion: Mastering the Fundamentals
Understanding log₄8, and logarithms in general, is crucial for anyone pursuing studies in mathematics, science, or engineering. This article has demonstrated several approaches to solving this specific problem, highlighting the importance of both conceptual understanding and practical application. By mastering these techniques, you can confidently tackle more challenging logarithmic problems and appreciate the significant role logarithms play in various aspects of our world. The key is to practice, experiment, and explore different methods to find the most efficient solution for each specific problem you encounter. Remember, even complex mathematical concepts become manageable with a systematic approach and a solid grasp of the underlying principles.
Latest Posts
Latest Posts
-
Why Data Classification Is Important
Sep 10, 2025
-
Is Mgoh2 A Strong Base
Sep 10, 2025
-
Are Roses Dicots Or Monocots
Sep 10, 2025
-
Where Do You Buy Alum
Sep 10, 2025
-
Is Angular Velocity A Vector
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Log Base 4 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.