Numbers That Multiply To 36
salachar
Sep 10, 2025 · 6 min read
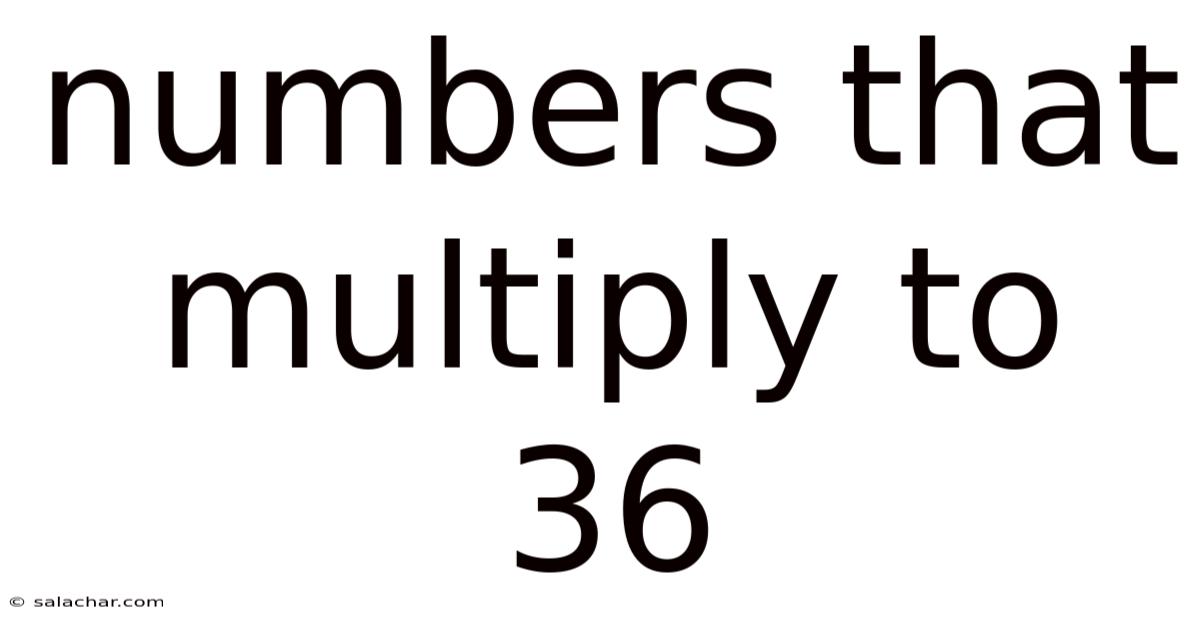
Table of Contents
Exploring the Factors and Multiples of 36: A Deep Dive into Number Theory
Finding all the numbers that multiply to 36 might seem like a simple arithmetic exercise. However, exploring this seemingly basic problem opens doors to a fascinating world of number theory, revealing concepts like prime factorization, factors, multiples, and even touching upon the elegance of mathematical relationships. This article will delve deep into the factors of 36, exploring their properties, providing practical examples, and explaining the underlying mathematical principles. We'll also address frequently asked questions and offer a concise summary.
Introduction: Unveiling the Multiplicative Partners of 36
The number 36, a seemingly ordinary integer, holds a wealth of mathematical secrets within its multiplicative structure. Understanding its factors – the numbers that divide evenly into 36 – is crucial for various mathematical operations and problem-solving. This exploration will go beyond simply listing the numbers; we'll investigate the patterns, relationships, and underlying mathematical principles that govern these factors. This understanding provides a foundational building block for more advanced concepts in number theory and algebra.
Finding the Factors of 36: A Systematic Approach
The most straightforward method to find all the numbers that multiply to 36 is through systematic factorization. We start by considering pairs of numbers whose product equals 36:
- 1 x 36: The simplest pair, representing the smallest and largest factors.
- 2 x 18: Introducing the factor 2, a prime number.
- 3 x 12: Here, we see the prime factor 3.
- 4 x 9: Both 4 and 9 are composite numbers (non-prime numbers greater than 1).
- 6 x 6: A unique pair, representing a perfect square factor.
This process reveals the complete set of factors for 36: 1, 2, 3, 4, 6, 9, 12, 18, and 36. Notice that these factors can be organized into pairs, except for 6 which pairs with itself. This signifies that 36 is a perfect square (6 x 6 = 36).
Prime Factorization: Deconstructing 36 into its Building Blocks
Prime factorization is a fundamental concept in number theory. It involves expressing a number as the product of its prime factors – prime numbers that, when multiplied together, result in the original number. For 36, the prime factorization is:
2² x 3²
This indicates that 36 is composed of two factors of 2 and two factors of 3. This prime factorization is unique to 36 and is essential for understanding many of its properties, including finding the number of divisors.
Calculating the Number of Divisors: A Formulaic Approach
The number of divisors of a number can be calculated directly from its prime factorization. If the prime factorization of a number n is given by:
n = p₁ᵃ¹ x p₂ᵃ² x ... x pₖᵃₖ
where pᵢ are distinct prime numbers and aᵢ are their respective exponents, then the number of divisors of n (denoted as τ(n) or d(n)) is given by:
τ(n) = (a₁ + 1)(a₂ + 1)...(aₖ + 1)
Applying this formula to 36 (2² x 3²):
τ(36) = (2 + 1)(2 + 1) = 3 x 3 = 9
This confirms our earlier finding that 36 has nine divisors.
Understanding Multiples of 36: Expanding the Horizons
While we've focused on factors, it's equally important to understand multiples of 36. Multiples are the products of 36 and any integer. The first few multiples of 36 are:
- 36 x 1 = 36
- 36 x 2 = 72
- 36 x 3 = 108
- 36 x 4 = 144
- and so on…
The multiples of 36 extend infinitely in both the positive and negative directions. They represent all numbers that are evenly divisible by 36.
Factors, Multiples, and the Relationship Between Them:
Factors and multiples have an inverse relationship. If a is a factor of b, then b is a multiple of a. For instance, since 6 is a factor of 36, 36 is a multiple of 6. This reciprocal relationship is fundamental to understanding divisibility and number relationships.
Practical Applications: Real-World Scenarios Involving the Factors of 36
The concept of factors and multiples isn't confined to theoretical mathematics; it has numerous practical applications:
-
Geometry: Calculating areas and volumes often involves finding factors. For instance, constructing a rectangle with an area of 36 square units requires considering the factor pairs of 36 (e.g., length 6 and width 6, length 9 and width 4, etc.).
-
Dividing Quantities: When dividing a quantity of 36 items into equal groups, the possible group sizes are determined by the factors of 36.
-
Number Puzzles and Games: Many mathematical puzzles and games involve finding factors or multiples, building problem-solving skills.
Beyond the Basics: Exploring Advanced Concepts
The seemingly simple problem of finding numbers that multiply to 36 can serve as a springboard for exploring more advanced mathematical concepts:
-
Greatest Common Divisor (GCD): Finding the greatest common divisor of two or more numbers is a crucial concept in simplifying fractions and solving various mathematical problems. For example, the GCD of 36 and 48 is 12.
-
Least Common Multiple (LCM): The least common multiple is the smallest number that is a multiple of two or more numbers. The LCM of 36 and 48 is 144.
-
Modular Arithmetic: Understanding factors and multiples is essential in modular arithmetic, which deals with remainders after division.
-
Number Theory Theorems: Many theorems in number theory relate to properties of factors and divisors, including the fundamental theorem of arithmetic.
Frequently Asked Questions (FAQs)
-
Q: What are the prime factors of 36?
- A: The prime factors of 36 are 2 and 3.
-
Q: Is 36 a perfect number?
- A: No, 36 is not a perfect number. A perfect number is a positive integer that is equal to the sum of its proper divisors (divisors excluding the number itself).
-
Q: How many divisors does 36 have?
- A: 36 has 9 divisors.
-
Q: What is the prime factorization of 36?
- A: The prime factorization of 36 is 2² x 3².
-
Q: What are some real-world applications of finding factors of 36?
- A: Real-world applications include geometry (calculating areas and volumes), dividing quantities into equal groups, and solving various mathematical puzzles.
Conclusion: The Enduring Significance of Factorization
The exploration of numbers that multiply to 36 has provided a comprehensive overview of fundamental number theory concepts. From basic factorization to prime factorization and the calculation of divisors, we've seen how a seemingly simple problem can unveil a wealth of mathematical richness. The concepts discussed—factors, multiples, prime factorization, GCD, and LCM—are not only important for a strong foundation in mathematics but also have far-reaching applications in various fields. Understanding these concepts fosters critical thinking, problem-solving skills, and a deeper appreciation for the elegance and interconnectedness of mathematical ideas. The journey into the world of factors and multiples of 36 has, hopefully, inspired further exploration of this fascinating branch of mathematics.
Latest Posts
Latest Posts
-
Is Wood A Pure Substance
Sep 10, 2025
-
Interrogative Declarative Imperative And Exclamatory
Sep 10, 2025
-
Pic For Dp On Whatsapp
Sep 10, 2025
-
Where To Buy Magnesium Chloride
Sep 10, 2025
-
Do Dark Colors Absorb Heat
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Numbers That Multiply To 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.