Square Root Of 12 25
salachar
Sep 14, 2025 · 5 min read
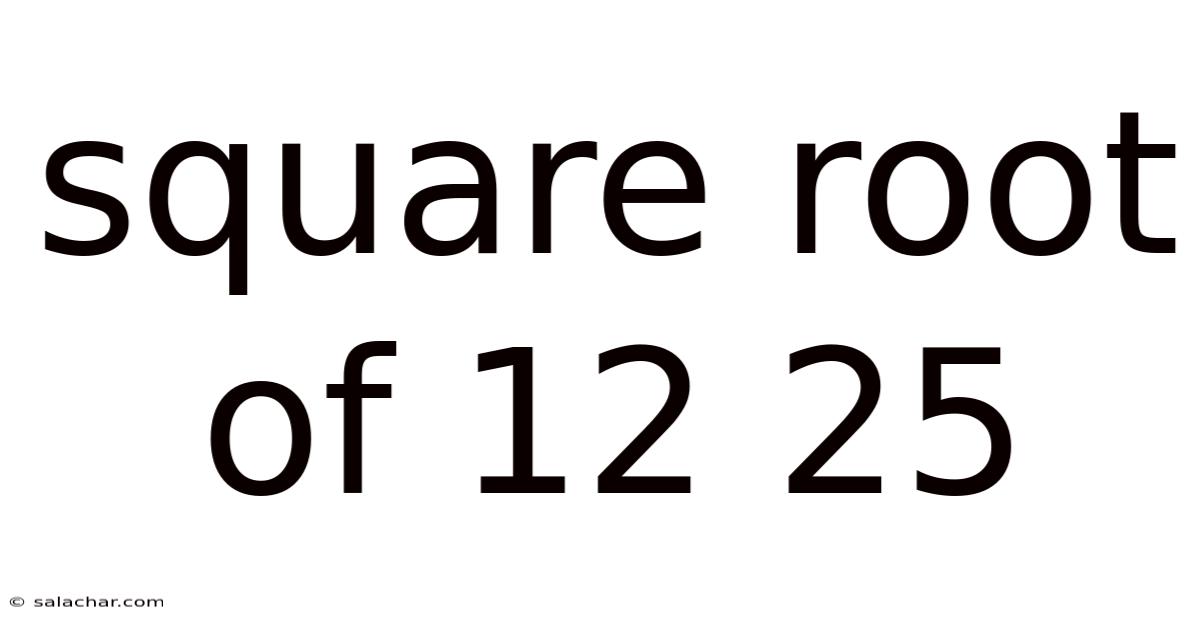
Table of Contents
Understanding the Square Root of 1225: A Comprehensive Guide
Finding the square root of a number might seem like a simple mathematical operation, but understanding the process and its implications can unlock a deeper appreciation for numbers and their relationships. This comprehensive guide will delve into calculating the square root of 1225, exploring different methods and highlighting the underlying mathematical concepts. We'll also address frequently asked questions and explore practical applications of square roots. By the end, you'll not only know the answer but also grasp the 'why' behind the calculation.
Introduction: What is a Square Root?
Before jumping into the specifics of the square root of 1225, let's establish a foundational understanding. A square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. Similarly, the square root of 16 is 4 because 4 x 4 = 16. It's important to note that all positive numbers have two square roots: a positive and a negative one. However, when we refer to "the" square root, we typically mean the positive square root.
Method 1: Prime Factorization
One effective method for finding the square root of 1225 is through prime factorization. This involves breaking down the number into its prime factors – numbers divisible only by 1 and themselves. Let's break down 1225:
- Divide by 5: 1225 ÷ 5 = 245
- Divide by 5 again: 245 ÷ 5 = 49
- Divide by 7: 49 ÷ 7 = 7
- Finally, 7 is a prime number:
Therefore, the prime factorization of 1225 is 5 x 5 x 7 x 7, or 5² x 7².
Now, because the square root involves finding a number that, when multiplied by itself, equals the original number, we can simplify:
√1225 = √(5² x 7²) = √5² x √7² = 5 x 7 = 35
Therefore, the square root of 1225 is 35.
Method 2: Estimation and Trial and Error
For smaller numbers, estimation and trial and error can be a viable approach. We know that 30 x 30 = 900 and 40 x 40 = 1600. Since 1225 falls between these two squares, we know the square root will be between 30 and 40. We can then systematically try numbers within this range:
- 31 x 31 = 961
- 32 x 32 = 1024
- 33 x 33 = 1089
- 34 x 34 = 1156
- 35 x 35 = 1225
This method confirms that the square root of 1225 is 35. While effective for smaller numbers, this method becomes less efficient for larger numbers.
Method 3: Using a Calculator
The simplest and most efficient method, especially for larger numbers, is using a calculator. Most calculators have a dedicated square root function (√). Simply input 1225 and press the square root button to obtain the answer: 35.
The Significance of Perfect Squares
The number 1225 is a perfect square because its square root is a whole number (35). Perfect squares are numbers that result from squaring a whole number. Understanding perfect squares is crucial in various mathematical contexts, including algebra, geometry, and number theory. Recognizing perfect squares can often simplify calculations and problem-solving.
Geometric Interpretation of Square Roots
The square root of a number also has a geometric interpretation. If you visualize a square with an area of 1225 square units, the length of each side of that square would be the square root of 1225, which is 35 units. This visual representation helps to connect the abstract concept of square roots to a tangible geometric reality.
Applications of Square Roots
Square roots find applications in many areas:
- Geometry: Calculating the sides of squares, right-angled triangles (using the Pythagorean theorem: a² + b² = c²), and other geometric figures.
- Physics: Formulas involving distance, velocity, and acceleration often utilize square roots.
- Engineering: Design and construction often require calculations involving square roots.
- Statistics: Standard deviation and other statistical measures involve square roots.
- Computer Graphics: Calculating distances and transformations in computer graphics frequently uses square roots.
Understanding Square Roots in Algebra
Square roots play a critical role in solving algebraic equations. For example, consider the equation x² = 1225. To solve for x, we take the square root of both sides: √x² = √1225, which gives us x = ±35. This highlights that algebraic equations often have multiple solutions, including both positive and negative square roots.
Advanced Concepts: Irrational Numbers and Approximations
While 1225 has a whole number square root, many numbers do not. The square roots of these numbers are irrational numbers – numbers that cannot be expressed as a simple fraction and have infinite, non-repeating decimal expansions. For example, the square root of 2 is an irrational number, approximately 1.41421356... For such numbers, we often rely on approximations obtained through iterative methods or calculators.
Frequently Asked Questions (FAQ)
-
Q: Is there only one square root for a number? A: No, every positive number has two square roots: a positive and a negative one. However, the principal square root (typically referred to as "the" square root) is the positive one.
-
Q: How can I calculate the square root of a negative number? A: The square root of a negative number is not a real number. It falls into the realm of imaginary numbers, denoted by 'i', where i² = -1.
-
Q: Are there different methods to find the square root besides the ones mentioned? A: Yes, there are more advanced methods, including numerical methods like the Newton-Raphson method, which are particularly useful for finding the square roots of very large numbers or irrational numbers.
-
Q: What if I need to find the square root of a decimal number? A: The same methods apply. You can use prime factorization (though it might be more complex), estimation, or a calculator. Calculators are particularly useful for handling decimal square roots efficiently.
Conclusion: Mastering Square Roots
Understanding the square root of 1225 – and square roots in general – extends beyond a simple calculation. It's about grasping fundamental mathematical concepts, appreciating the relationships between numbers, and recognizing the diverse applications of square roots across various fields. Through prime factorization, estimation, or the simple use of a calculator, finding the square root of 1225 (which is 35) provides a stepping stone to understanding more complex mathematical concepts and problem-solving strategies. The ability to calculate and interpret square roots is a valuable skill that will continue to serve you well in your mathematical journey.
Latest Posts
Latest Posts
-
What Is 15 Of 245
Sep 14, 2025
-
Example Of Connotation In Literature
Sep 14, 2025
-
I Love U My Hubby
Sep 14, 2025
-
Making A Difference Starfish Story
Sep 14, 2025
-
Food That Start With T
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 12 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.