Square Root Of 150 Simplified
salachar
Sep 15, 2025 · 6 min read
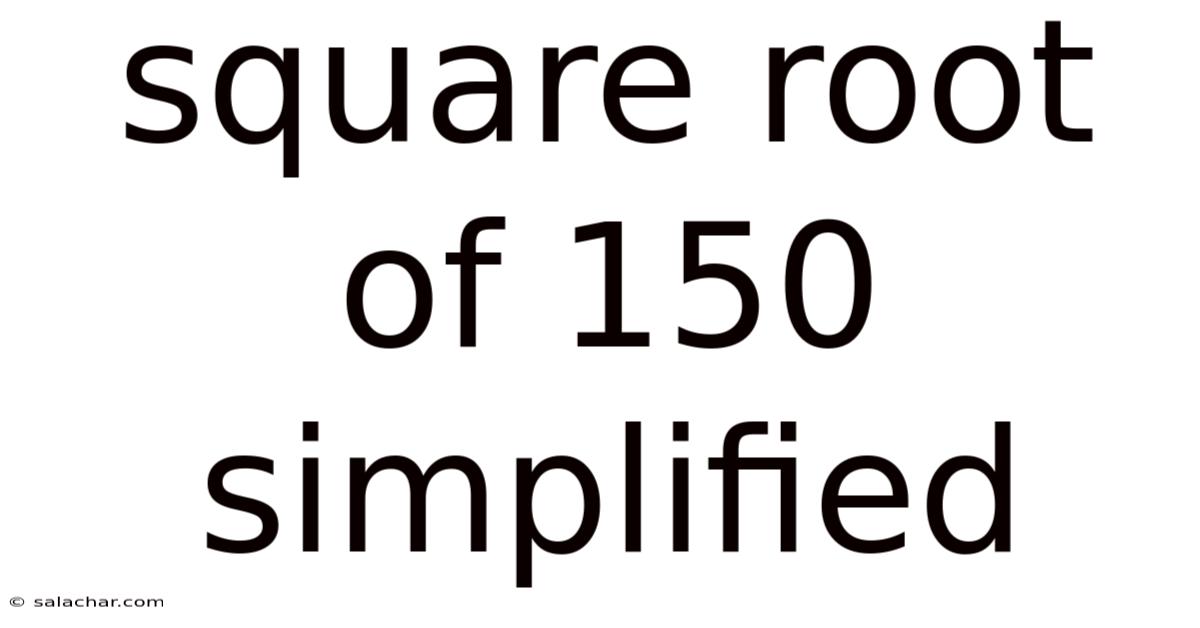
Table of Contents
Unveiling the Secrets of √150: A Comprehensive Guide to Simplifying Square Roots
Finding the square root of a number, especially one like 150 that isn't a perfect square, can seem daunting at first. But understanding the process of simplifying square roots unlocks a powerful tool in mathematics and opens doors to more advanced concepts. This comprehensive guide will take you step-by-step through simplifying √150, explaining the underlying principles and providing practical examples to build your confidence. We'll explore the concept of prime factorization, its crucial role in simplifying radicals, and address common misconceptions along the way. By the end, you'll not only know the simplified form of √150 but also possess the skills to tackle similar problems with ease.
Understanding Square Roots and Perfect Squares
Before diving into the simplification of √150, let's establish a solid foundation. A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. A perfect square is a number that results from squaring an integer (a whole number). Examples of perfect squares include 1 (1 x 1), 4 (2 x 2), 9 (3 x 3), 16 (4 x 4), and so on.
Numbers like 150, however, are not perfect squares. This means their square roots are not whole numbers but rather irrational numbers – numbers that cannot be expressed as a simple fraction. Simplifying such square roots involves expressing them in their most concise and manageable form.
The Power of Prime Factorization
The key to simplifying square roots like √150 lies in prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 150:
- Start with the smallest prime number, 2: 150 is an even number, so it's divisible by 2. 150 ÷ 2 = 75.
- Move to the next prime number, 3: 75 is divisible by 3. 75 ÷ 3 = 25.
- Continue with prime numbers: 25 is divisible by 5. 25 ÷ 5 = 5. 5 is a prime number itself.
Therefore, the prime factorization of 150 is 2 x 3 x 5 x 5, or 2 x 3 x 5².
Simplifying √150: A Step-by-Step Approach
Now that we have the prime factorization of 150, we can simplify its square root:
- Rewrite the square root using the prime factorization: √150 = √(2 x 3 x 5²)
- Identify pairs of identical factors: Notice that we have a pair of 5s (5²).
- Bring out pairs as whole numbers: Since √(5²) = 5, we can bring one 5 outside the square root symbol.
- Leave remaining factors under the square root: The factors 2 and 3 remain under the square root.
Therefore, the simplified form of √150 is 5√6.
Visualizing the Simplification
Imagine a square with an area of 150 square units. Simplifying √150 is like finding the side length of this square. By factoring 150 into 2 x 3 x 5 x 5, we can visualize the square as being composed of smaller squares and rectangles. The pair of 5s represents a 5 x 5 square (area 25), which contributes a side length of 5 to our overall square root. The remaining factors, 2 and 3, represent a rectangle with area 6, leaving its dimensions still under the square root.
Addressing Common Mistakes
A frequent mistake is incorrectly simplifying square roots by just dividing the original number by a perfect square. For example, some might incorrectly state that √150 = √(25 x 6) = 5√6, without understanding why this step is valid due to the prime factorization. Remember, the process hinges on identifying pairs of identical factors within the prime factorization, not simply dividing by any perfect square.
Expanding the Concept: Simplifying Other Square Roots
The method we used for simplifying √150 applies to other square roots as well. Let's consider another example: √72
- Prime factorization of 72: 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
- Rewrite the square root: √72 = √(2³ x 3²)
- Identify pairs: We have a pair of 2s and a pair of 3s.
- Simplify: √72 = √(2² x 2 x 3²) = 2 x 3√2 = 6√2
Beyond the Basics: Working with Variables
The principles of prime factorization and simplifying square roots extend to expressions involving variables. For example, let's simplify √(12x²y³):
- Prime factorization: 12 = 2² x 3; x² = x x x; y³ = y x y x y
- Rewrite: √(12x²y³) = √(2² x 3 x x² x y³)
- Identify pairs: We have a pair of 2s, a pair of xs, and a pair of ys.
- Simplify: √(12x²y³) = 2xy√(3y)
Frequently Asked Questions (FAQ)
Q: Why is prime factorization essential for simplifying square roots?
A: Prime factorization allows us to break down a number into its fundamental building blocks. This makes it easier to identify pairs of identical factors, which are crucial for simplifying the square root. Without prime factorization, we might miss potential simplifications.
Q: What if there are no pairs of factors after prime factorization?
A: If, after prime factorization, there are no pairs of identical factors, the square root is already in its simplest form. For example, √17 is already simplified because 17 is a prime number.
Q: Can I simplify square roots with fractions?
A: Yes, you can. Simplify the numerator and denominator separately, then simplify the resulting square root. For example, √(4/9) = √4 / √9 = 2/3. For more complex fractional square roots, consider simplifying the fraction within the square root first before applying the prime factorization method.
Q: Are there any shortcuts for simplifying square roots?
A: While prime factorization is the most fundamental method, with practice, you might develop an intuition for recognizing perfect square factors within a number. However, relying solely on intuition can lead to mistakes, particularly with larger numbers. The systematic approach of prime factorization ensures accuracy.
Conclusion: Mastering the Art of Square Root Simplification
Simplifying square roots, initially appearing complex, becomes a manageable and even enjoyable process with a solid understanding of prime factorization. This methodical approach not only provides the correct answer but also fosters a deeper appreciation of mathematical principles. By consistently practicing the steps outlined in this guide and by addressing common misconceptions, you'll not only confidently simplify square roots like √150 but also build a stronger foundation for more advanced mathematical concepts. Remember that mathematical proficiency comes with persistent practice and a curious mind – keep exploring, keep learning, and keep simplifying!
Latest Posts
Latest Posts
-
Triangular Prism Real Life Examples
Sep 15, 2025
-
2 Root 3 2
Sep 15, 2025
-
P V R Full Form
Sep 15, 2025
-
What Is A Inexhaustible Resource
Sep 15, 2025
-
Darwins Tubercle Dominant Or Recessive
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 150 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.