Square Root Of 17 Simplified
salachar
Sep 09, 2025 · 5 min read
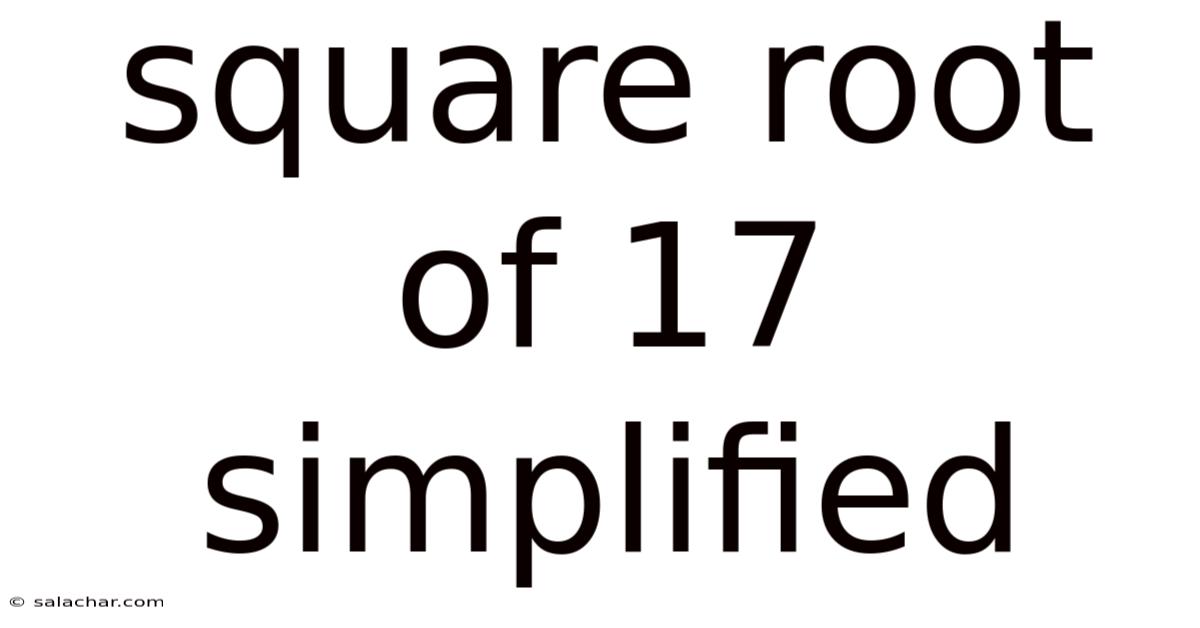
Table of Contents
Unveiling the Mystery: Simplifying the Square Root of 17
Finding the square root of 17 might seem like a straightforward task, especially with the readily available calculators. However, understanding the process of simplifying square roots, particularly those that don't yield whole numbers, reveals a deeper appreciation for mathematical principles. This article delves into the intricacies of simplifying √17, exploring its approximate value, the reasons behind its irrationality, and the methods used to approach such calculations both manually and conceptually. We'll also explore practical applications and address frequently asked questions.
Understanding Square Roots and Irrational Numbers
Before we tackle √17 specifically, let's establish a foundational understanding. A square root (√) of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. However, not all square roots result in neat whole numbers or simple fractions. Numbers like √17 fall into a category called irrational numbers.
Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representation goes on forever without repeating. This is precisely why simplifying √17 doesn't lead to a concise, exact answer like √9 does. Instead, we aim to simplify it to its most concise radical form and understand its approximate decimal value.
Why √17 Cannot Be Simplified Further
Unlike square roots like √16 (which simplifies to 4) or √25 (which simplifies to 5), √17 doesn't have any perfect square factors other than 1. To simplify a square root, we look for perfect square factors within the radicand (the number under the square root symbol). The prime factorization of 17 is simply 17. It's a prime number; it's only divisible by 1 and itself. This means there are no perfect squares (like 4, 9, 16, 25, etc.) that divide evenly into 17. Therefore, √17 is already in its simplest radical form.
This doesn't mean we can't work with it or understand its value; it simply means we can't express it as a whole number or a fraction.
Approximating the Value of √17
Since we can't simplify √17 to a more elegant form, we can approximate its value using several methods:
-
Using a Calculator: The simplest and most accurate method is to use a calculator. √17 ≈ 4.1231
-
Estimation: We know that 4² = 16 and 5² = 25. Since 17 lies between 16 and 25, √17 must lie between 4 and 5. We can refine this estimation by noticing that 17 is closer to 16 than to 25, suggesting that √17 is closer to 4 than to 5.
-
Babylonian Method (or Heron's Method): This iterative method provides a progressively more accurate approximation of square roots. Let's illustrate it for √17:
- Start with an initial guess: Let's guess 4.
- Improve the guess: Divide 17 by the guess (17/4 = 4.25).
- Average the guess and the result: Average 4 and 4.25: (4 + 4.25)/2 = 4.125
- Repeat: Now, use 4.125 as the new guess and repeat steps 2 and 3. The more iterations you perform, the closer your approximation gets to the actual value.
Understanding √17 in Geometric Contexts
The square root of 17 has a clear geometrical interpretation. Imagine a right-angled triangle with legs of length 1 and 4. By the Pythagorean theorem (a² + b² = c²), the hypotenuse (c) would have a length of √(1² + 4²) = √17. Therefore, √17 represents the length of the hypotenuse in this specific right-angled triangle. This geometric representation provides a tangible understanding of the value, even if we can't express it precisely as a fraction.
Practical Applications of √17
While √17 might not appear as frequently as simpler square roots in everyday calculations, it does arise in various applications, including:
-
Physics and Engineering: Calculations involving vectors, distances, and forces often involve square roots of non-perfect squares.
-
Computer Graphics: Determining distances and positions in 2D or 3D space frequently utilizes square roots.
-
Mathematics: In advanced mathematical concepts like calculus and geometry, irrational numbers are fundamental.
Frequently Asked Questions (FAQs)
Q: Can √17 be expressed as a decimal?
A: While it can't be expressed as a finite or repeating decimal, it can be approximated to any desired level of accuracy using a calculator or iterative methods like the Babylonian method.
Q: Is √17 a rational or irrational number?
A: √17 is an irrational number because it cannot be expressed as a ratio of two integers. Its decimal representation is non-terminating and non-repeating.
Q: How can I simplify √17 without using a calculator?
A: You can't simplify √17 further in the traditional sense of finding perfect square factors. However, you can approximate its value using estimation or iterative methods like the Babylonian method.
Q: What are some other examples of irrational square roots?
A: Many square roots of non-perfect squares are irrational, such as √2, √3, √5, √6, √7, and so on. Essentially, any square root of a number that is not a perfect square is irrational.
Conclusion
Simplifying √17, although seemingly a simple task, offers a valuable insight into the nature of irrational numbers and the limitations of expressing certain mathematical concepts using finite fractions or decimals. While we cannot express √17 in a simpler radical form, understanding its approximate value and its geometrical interpretation provides a deeper comprehension of this number’s significance. Whether you're a student grappling with basic algebra or an engineer tackling complex calculations, grasping the concept of simplifying (or in this case, the inability to simplify) square roots is a crucial element of mathematical proficiency. The exploration of √17, therefore, goes beyond a simple calculation and acts as a gateway to a wider appreciation for the intricacies and elegance of mathematics.
Latest Posts
Latest Posts
-
How To Make Origami Stuff
Sep 09, 2025
-
Log To The Base 3
Sep 09, 2025
-
Funny Things About The Internet
Sep 09, 2025
-
Use Has In A Sentence
Sep 09, 2025
-
What Atomic Number Has 7
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 17 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.