Square Root Of 2 500
salachar
Sep 09, 2025 · 6 min read
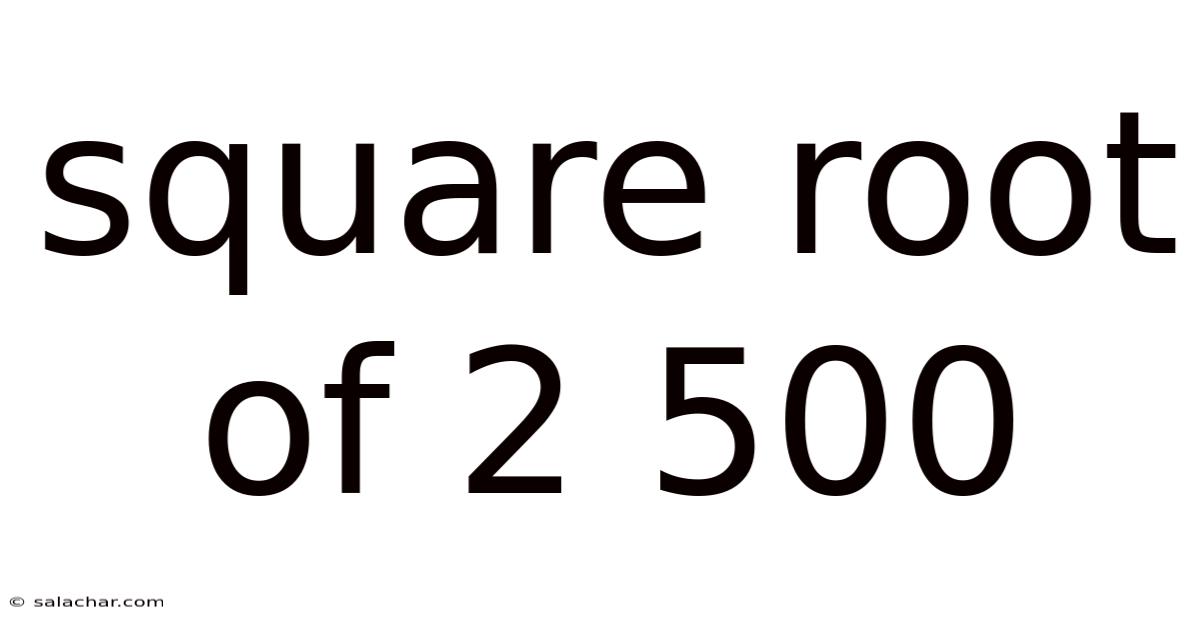
Table of Contents
Unveiling the Mystery: Understanding the Square Root of 2500
The square root of a number is a value that, when multiplied by itself, gives the original number. Finding the square root of 2500 might seem like a simple mathematical task, but exploring its solution opens doors to a deeper understanding of fundamental mathematical concepts, including perfect squares, prime factorization, and even the history of mathematics. This comprehensive guide will not only show you how to calculate the square root of 2500 but also explore the broader mathematical context surrounding it.
Understanding Perfect Squares
Before diving into the specifics of calculating the square root of 2500, let's establish a foundational understanding of perfect squares. A perfect square is the result of squaring a whole number (an integer). For example:
- 1² = 1
- 2² = 4
- 3² = 9
- 4² = 16
- and so on...
Recognizing perfect squares is crucial for quickly calculating square roots. The number 2500 itself is a perfect square, which simplifies the calculation considerably.
Calculating the Square Root of 2500: The Simple Approach
The most straightforward method for finding the square root of 2500 is to recognize it as a perfect square. Since 50 multiplied by 50 equals 2500 (50² = 2500), the square root of 2500 is 50.
This method is effective for relatively small perfect squares. However, for larger numbers or numbers that are not perfect squares, more sophisticated methods are needed.
Prime Factorization: A Deeper Dive
Prime factorization is a powerful technique in number theory. It involves breaking down a number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 2500:
- Start with the smallest prime number, 2: 2500 is an even number, so it's divisible by 2. 2500 / 2 = 1250.
- Continue with 2: 1250 is also even. 1250 / 2 = 625.
- Now, move to the next prime number, 5: 625 ends in 5, indicating divisibility by 5. 625 / 5 = 125.
- Continue with 5: 125 is also divisible by 5. 125 / 5 = 25.
- Continue with 5: 25 is divisible by 5. 25 / 5 = 5.
- Finally, we have our last prime factor, 5.
Therefore, the prime factorization of 2500 is 2 x 2 x 5 x 5 x 5 x 5, or 2² x 5⁴.
How does this help us find the square root? When finding the square root, we essentially look for pairs of factors. In our prime factorization, we have a pair of 2s and two pairs of 5s. Taking one factor from each pair, we get 2 x 5 x 5 = 50. This confirms our earlier finding that the square root of 2500 is 50.
Approximation Methods for Non-Perfect Squares
While 2500 is a perfect square, let's consider how to approximate the square root of a number that isn't a perfect square. Several methods exist, including:
-
Babylonian Method (or Heron's Method): This iterative method refines an initial guess to get closer to the actual square root. It involves repeatedly averaging the guess and the number divided by the guess.
-
Linear Approximation: This simpler method uses the slope of the square root function to estimate the square root based on a known nearby perfect square.
-
Using a Calculator or Computer: Modern technology provides the easiest way to calculate square roots to a high degree of accuracy.
These methods are particularly useful for dealing with numbers that are not perfect squares.
The Square Root of 2500 in Different Number Systems
While our calculations have been in the decimal system (base 10), it's interesting to consider how the square root of 2500 might be represented in other number systems:
-
Binary (base 2): 2500 in binary is 100111000100. Finding the square root in binary requires a different approach, but the result would still be equivalent to 50 (110010 in binary).
-
Hexadecimal (base 16): 2500 in hexadecimal is 9C4. Again, the square root in hexadecimal would represent the decimal equivalent of 50.
This illustrates that the fundamental mathematical concept of the square root remains consistent across different number systems.
The Historical Significance of Square Roots
The concept of square roots has a rich history, tracing back to ancient civilizations. The Babylonians, for instance, developed sophisticated algorithms for approximating square roots. The Greeks, notably Pythagoras and his followers, extensively studied square roots and their geometric interpretations. The discovery of irrational numbers, such as the square root of 2, significantly impacted the development of mathematics. The square root of 2, famously, cannot be expressed as a simple fraction, challenging the then-prevailing understanding of numbers.
The calculation of square roots, particularly of larger numbers, has been significantly aided by the development of computational tools. From slide rules to modern calculators and computers, the quest for efficient computation has driven mathematical advancements.
Applications of Square Roots
Understanding square roots has vast applications across numerous fields:
-
Physics: Calculating velocity, distance, and acceleration often involves square roots. Equations in mechanics, optics, and other branches of physics frequently utilize square roots.
-
Engineering: In structural engineering, calculating stress and strain often requires working with square roots. Civil, mechanical, and electrical engineers use square roots in various applications.
-
Geometry: Finding the lengths of diagonals in rectangles, squares, and other geometric shapes involves the Pythagorean theorem, which relies heavily on square roots.
-
Finance: In finance, calculating standard deviation and variance in investment analysis often involves square roots.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest way to find the square root of 2500?
- A: The simplest way is to recognize that 2500 is a perfect square, specifically 50². Therefore, the square root is 50.
-
Q: How do I calculate the square root of a number that is not a perfect square?
- A: For non-perfect squares, approximation methods like the Babylonian method or using a calculator are necessary.
-
Q: What are the practical applications of square roots?
- A: Square roots are widely applied in physics, engineering, geometry, finance, and many other fields. They are essential for solving various mathematical problems in these domains.
-
Q: Is the square root of 2500 a rational or irrational number?
- A: The square root of 2500 (which is 50) is a rational number because it can be expressed as a fraction (50/1). Irrational numbers, like the square root of 2, cannot be expressed as a simple fraction.
-
Q: What is the difference between a square root and a cube root?
- A: A square root is a number that, when multiplied by itself, gives the original number. A cube root is a number that, when multiplied by itself three times, gives the original number.
Conclusion
Finding the square root of 2500, seemingly a simple arithmetic problem, provides a gateway to a wealth of mathematical concepts. From the basic understanding of perfect squares and prime factorization to more advanced approximation techniques and the historical context of square root calculations, this exploration has highlighted the fundamental role of square roots in mathematics and their far-reaching applications in various fields. Whether you're a student grappling with basic arithmetic or a professional needing to solve complex equations, a thorough understanding of square roots is crucial for success in numerous endeavors. The seemingly simple question of "What is the square root of 2500?" thus opens a window into the beauty and utility of mathematics.
Latest Posts
Latest Posts
-
Difference Between Kva And Kw
Sep 09, 2025
-
Is Area Squared Or Cubed
Sep 09, 2025
-
When Is Winter In India
Sep 09, 2025
-
What Is Divisible By 57
Sep 09, 2025
-
Meaning Of Being And Been
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.