Square Root Of 289 Simplified
salachar
Sep 14, 2025 · 6 min read
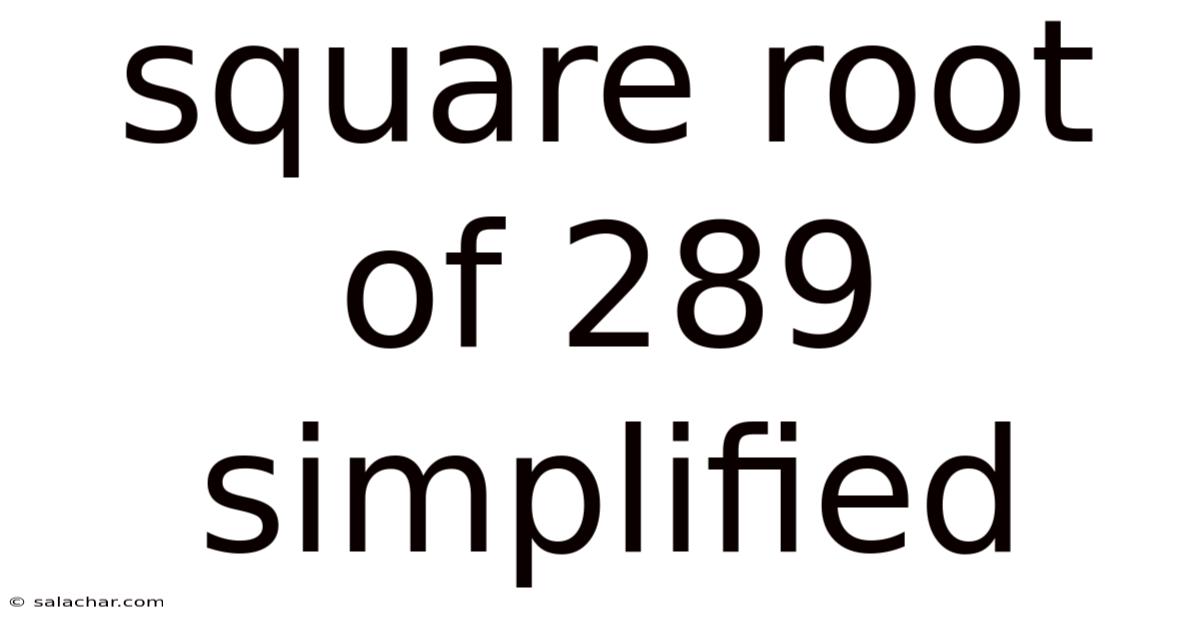
Table of Contents
Unveiling the Secrets of √289: A Comprehensive Guide to Simplifying Square Roots
Finding the square root of a number might seem like a simple arithmetic task, but understanding the underlying principles and methods can unlock a deeper appreciation for mathematics. This comprehensive guide delves into the process of simplifying the square root of 289 (√289), exploring various techniques and providing a solid foundation for tackling more complex square root problems. We'll go beyond simply stating the answer and delve into the "why" behind the methods, making this understanding accessible to everyone from beginners to those looking to refresh their knowledge.
Understanding Square Roots: A Quick Refresher
Before we dive into simplifying √289, let's solidify our understanding of what a square root actually represents. The square root of a number is a value that, when multiplied by itself, results in the original number. For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. In simpler terms, it's finding the side length of a square given its area.
This concept extends to all non-negative numbers. While the square root of a negative number involves imaginary numbers (denoted by 'i'), we'll focus on positive real numbers in this article.
Method 1: Prime Factorization – The Foundation of Simplification
The most fundamental approach to simplifying square roots involves prime factorization. This method breaks down a number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this to 289:
-
Find the Prime Factors: We need to find the prime numbers that multiply together to equal 289. We can start by trying small prime numbers: 289 is not divisible by 2 (it's not even), nor by 3 (the sum of its digits, 2+8+9=19, is not divisible by 3). Let's try 17: 289 ÷ 17 = 17. Therefore, the prime factorization of 289 is 17 x 17, or 17².
-
Simplify the Square Root: Now that we have the prime factorization, we can rewrite √289 as √(17 x 17) or √(17²). Since the square root and the square cancel each other out, the simplified answer is simply 17.
Therefore, √289 = 17.
Method 2: Using a Calculator – A Quick and Convenient Approach
While prime factorization provides a deeper understanding, using a calculator offers a quick and efficient way to find the square root of any number. Most scientific and even basic calculators have a square root function (usually denoted by √ or √x). Simply enter 289 and press the square root button; the calculator will directly provide the answer, 17. This method is particularly useful when dealing with larger numbers or when speed is crucial.
Method 3: Estimation and Perfect Squares – Building Intuition
Before resorting to a calculator, developing an intuitive sense for perfect squares can help estimate the square root. Perfect squares are numbers that result from squaring an integer (e.g., 1, 4, 9, 16, 25, etc.). By recognizing the perfect squares surrounding 289, we can make a reasonable estimate.
We know that 17² = 289. While this specific case is easily identifiable, this method helps build intuition for estimating the square root of numbers that aren't perfect squares. For example, if you were asked to estimate √300, you could reason that it's slightly larger than √289 (which is 17), and considerably smaller than √324 (which is 18).
Understanding the Concept of Simplification: Beyond Perfect Squares
While 289 is a perfect square, making the simplification straightforward, many numbers are not. Let's consider how to simplify a square root when the number isn't a perfect square. For example, let's examine √72.
-
Prime Factorization: The prime factorization of 72 is 2³ x 3².
-
Pairing Factors: We look for pairs of identical prime factors within the factorization. We have a pair of 3s (3²).
-
Simplifying: We can rewrite √72 as √(2³ x 3²) = √(2² x 2 x 3²) = √(2²) x √(3²) x √2 = 2 x 3 x √2 = 6√2.
Therefore, √72 simplifies to 6√2. This shows that even if a number isn't a perfect square, we can simplify the radical expression by finding perfect square factors.
This process highlights that simplification involves extracting perfect square factors from under the square root symbol. This leaves only prime factors without pairs under the radical sign, leading to a more concise and simplified form.
Expanding on the Concept: Dealing with Variables in Square Roots
The principles of simplification extend beyond numerical values to include variables. Consider simplifying √(16x⁴y²).
-
Factorization: We factor the expression under the square root: √(4² x x⁴ x y²)
-
Pairing: We identify pairs of identical factors: (4²), (x² x x²), and (y²).
-
Simplification: Extracting the paired factors from the square root: 4 x x² x y = 4x²y.
Therefore, √(16x⁴y²) simplifies to 4x²y. Note that if there were leftover variables without pairs, they would remain under the square root. For example, simplifying √(25x³y⁴) would result in 5xy²√x.
Applications of Square Roots: Real-World Examples
Understanding square roots isn't merely an academic exercise; it has numerous applications in various fields:
- Geometry: Calculating the diagonal of a square or rectangle, finding the distance between two points using the Pythagorean theorem.
- Physics: Determining the velocity or energy in various physical scenarios.
- Engineering: Calculating structural dimensions and forces.
- Computer Graphics: Used extensively in calculations related to 2D and 3D graphics.
Frequently Asked Questions (FAQs)
-
Q: What if the number under the square root is negative?
- A: The square root of a negative number involves imaginary numbers. The imaginary unit, i, is defined as √(-1). Therefore, √(-9) would be represented as 3i.
-
Q: Can I use a calculator for every square root problem?
- A: While calculators provide a quick solution, understanding the underlying methods of prime factorization and simplification is crucial for comprehending the mathematical concepts and tackling more complex problems involving variables and expressions.
-
Q: Why is simplification important?
- A: Simplifying square roots provides a more concise and manageable form, making further calculations and analysis easier. It also helps in understanding the fundamental structure of the number.
-
Q: Are there any online tools to check my simplification?
- A: While specific online tools aren't recommended here, many math websites and calculators can help verify your simplification steps. It's helpful to work through the problems independently and then use such tools for verification rather than relying on them entirely.
Conclusion: Mastering the Art of Simplifying Square Roots
Simplifying the square root of 289, as we've seen, is relatively straightforward due to it being a perfect square. However, the techniques and principles we've explored extend far beyond this specific example. Mastering prime factorization and understanding how to extract perfect squares from under the radical sign are essential skills for anyone seeking a deeper understanding of mathematics and its practical applications. By combining these methods and cultivating an intuitive sense for perfect squares, you can confidently tackle a wide range of square root problems, solidifying your mathematical foundation and expanding your problem-solving abilities. Remember that practice is key to mastering this skill. Try simplifying various square roots, starting with simpler examples and gradually progressing to more complex ones. The more you practice, the more intuitive and efficient you'll become.
Latest Posts
Latest Posts
-
Convert Oz To Troy Oz
Sep 14, 2025
-
At 6 00 In The Morning
Sep 14, 2025
-
Citric Acid And Sodium Hydroxide
Sep 14, 2025
-
Real Life Examples Of Inertia
Sep 14, 2025
-
Short Rhyme Poems For Teachers
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 289 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.