Square Root Of 5 6
salachar
Sep 08, 2025 · 5 min read
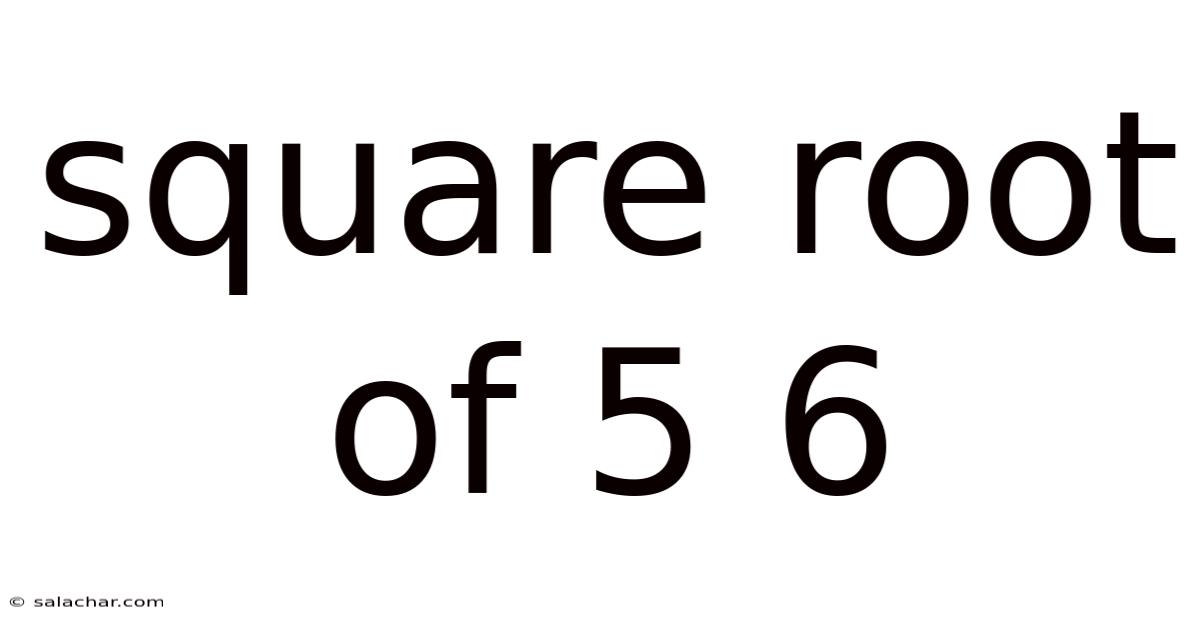
Table of Contents
Unveiling the Mysteries of the Square Root of 56: A Deep Dive
The square root of 56, denoted as √56, is a number that, when multiplied by itself, equals 56. While seemingly simple, exploring this seemingly straightforward concept opens doors to a fascinating world of mathematics, touching upon topics like prime factorization, estimation techniques, and the nature of irrational numbers. This article will provide a comprehensive understanding of √56, exploring its calculation, applications, and the broader mathematical principles it exemplifies.
Understanding Square Roots
Before delving into the specifics of √56, let's refresh our understanding of square roots. A square root of a number 'x' is a value that, when multiplied by itself, results in 'x'. For instance, the square root of 9 (√9) is 3 because 3 x 3 = 9. However, not all square roots are whole numbers. Many numbers, including 56, have square roots that are irrational numbers – numbers that cannot be expressed as a simple fraction and have decimal representations that continue infinitely without repeating.
Calculating √56: The Prime Factorization Approach
One common method for approximating the square root of a number like 56 involves prime factorization. This method breaks down the number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization: Let's find the prime factors of 56:
56 = 2 x 28 = 2 x 2 x 14 = 2 x 2 x 2 x 7 = 2³ x 7
-
Simplifying the Square Root: Now, we can rewrite √56 using the prime factorization:
√56 = √(2³ x 7) = √(2² x 2 x 7) = 2√(2 x 7) = 2√14
This simplified form, 2√14, tells us that the square root of 56 is twice the square root of 14. While this doesn't give us a precise decimal value, it presents a simplified radical form often preferred in mathematical contexts.
Approximating √56: Numerical Methods
Since √56 is irrational, we can only approximate its decimal value. Several methods can achieve this, including:
-
Using a Calculator: The simplest approach is to use a calculator with a square root function. This will provide a decimal approximation, typically accurate to several decimal places. A calculator will show that √56 ≈ 7.4833.
-
Babylonian Method (or Heron's Method): This iterative method provides increasingly accurate approximations. It starts with an initial guess and refines it through repeated calculations. Let's illustrate this:
-
Initial Guess: Let's start with an initial guess of 7 (since 7² = 49, which is close to 56).
-
Iteration 1: Divide 56 by the guess (56/7 = 8). Average the result with the initial guess: (7 + 8)/2 = 7.5.
-
Iteration 2: Repeat the process using the new guess (7.5). 56/7.5 ≈ 7.4667. Average: (7.5 + 7.4667)/2 ≈ 7.4833
With each iteration, the approximation becomes more accurate. Further iterations would yield even closer approximations to the actual value of √56.
-
-
Linear Approximation: This method uses the tangent line to the curve y = √x at a nearby point to estimate the square root. While less precise than the Babylonian method, it's conceptually simpler.
Understanding the Irrational Nature of √56
As previously mentioned, √56 is an irrational number. This means it cannot be expressed as a fraction of two integers (a/b, where 'a' and 'b' are integers and 'b' is not zero). Its decimal representation is non-terminating and non-repeating, meaning it continues infinitely without exhibiting a repeating pattern. This is a fundamental characteristic of many square roots, particularly those of non-perfect squares (numbers that are not the square of an integer).
Applications of √56 and Related Concepts
The square root, and more broadly, the concept of radicals, finds numerous applications across various fields:
-
Geometry: Calculating lengths of diagonals in squares and rectangles, or determining the hypotenuse of a right-angled triangle using the Pythagorean theorem (a² + b² = c²) often involves square roots.
-
Physics: Many physics formulas utilize square roots, such as calculations involving velocity, energy, and momentum. For example, calculating the speed of an object based on kinetic energy involves a square root.
-
Engineering: In structural engineering, designing stable and load-bearing structures requires precise calculations involving square roots to handle stress and strain.
-
Computer Graphics: Generating realistic graphics and simulations often relies on extensive mathematical calculations, including square roots, for accurate representations of shapes, movements, and interactions.
-
Finance: Calculating compound interest and various financial models often involve the use of roots and powers.
Frequently Asked Questions (FAQs)
-
Q: Is √56 a rational or irrational number?
- A: √56 is an irrational number.
-
Q: How can I calculate √56 without a calculator?
- A: You can use methods like the Babylonian method or linear approximation to obtain an approximate value. Prime factorization simplifies the radical but doesn't provide a decimal approximation.
-
Q: What is the difference between √56 and 56²?
- A: √56 represents the square root of 56 (the number that, when multiplied by itself, equals 56). 56² represents 56 raised to the power of 2 (56 multiplied by itself), which equals 3136.
-
Q: Can √56 be simplified further than 2√14?
- A: No, 2√14 is the simplest radical form for √56.
Conclusion: A Deeper Appreciation of √56
While at first glance, the square root of 56 may seem like a simple mathematical concept, a closer examination reveals a deeper richness. Understanding its calculation through prime factorization, exploring approximation techniques like the Babylonian method, and recognizing its irrational nature all contribute to a more profound understanding of numbers and their properties. The widespread applications of square roots across various scientific and engineering disciplines highlight their importance in solving real-world problems. Hopefully, this exploration has not only provided a clear understanding of √56 but also sparked a curiosity to delve deeper into the fascinating world of mathematics.
Latest Posts
Latest Posts
-
Barium Chloride And Sodium Sulphate
Sep 09, 2025
-
Shiba Inu Black Lab Mix
Sep 09, 2025
-
What Is A Template Strand
Sep 09, 2025
-
Electron Dot Diagram For Beryllium
Sep 09, 2025
-
Henrys Law Vs Raoults Law
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.