What Is 0.0098 In Scientific
salachar
Sep 04, 2025 · 5 min read
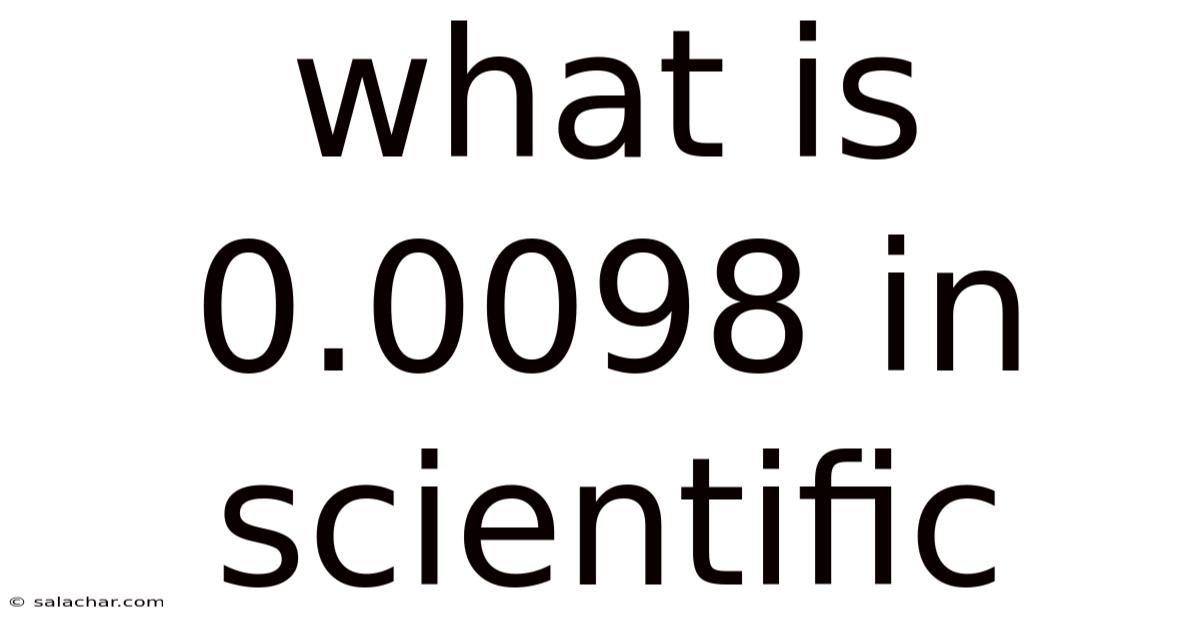
Table of Contents
Decoding 0.0098: A Deep Dive into Scientific Notation
Understanding scientific notation is crucial for anyone working with very large or very small numbers, common in fields like science, engineering, and finance. This article will thoroughly explore how to express the number 0.0098 in scientific notation, explaining the process step-by-step and delving into the underlying principles. We'll cover not only the conversion but also the broader implications and applications of scientific notation. By the end, you'll be confident in converting numbers to and from scientific notation and grasping its importance in various disciplines.
Understanding Scientific Notation
Scientific notation, also known as standard form, is a standardized way of writing numbers that are either very large or very small. It's based on powers of 10, making it concise and efficient for representing numbers that would otherwise be cumbersome to write in standard decimal form. The general format is:
N x 10<sup>e</sup>
Where:
- N is a number between 1 and 10 (but not including 10 itself). This is called the coefficient or mantissa.
- e is an integer exponent, representing the power of 10. This indicates how many places the decimal point has been moved.
Converting 0.0098 to Scientific Notation: A Step-by-Step Guide
Let's break down how to convert 0.0098 into scientific notation.
Step 1: Identify the Coefficient (N)
We need to reposition the decimal point to create a number between 1 and 10. In 0.0098, we move the decimal point three places to the right, resulting in 9.8. Therefore, our coefficient (N) is 9.8.
Step 2: Determine the Exponent (e)
Since we moved the decimal point three places to the right, the exponent (e) will be -3. Moving the decimal point to the right indicates a negative exponent because the original number is less than 1. If we had moved it to the left, the exponent would be positive.
Step 3: Write the Scientific Notation
Combining the coefficient and exponent, we get the scientific notation for 0.0098:
9.8 x 10<sup>-3</sup>
Why Use Scientific Notation?
The benefits of scientific notation are numerous:
-
Conciseness: It provides a compact way to represent extremely large or small numbers. Imagine writing out Avogadro's number (approximately 602,214,076,000,000,000,000,000) without scientific notation!
-
Clarity: It improves readability and reduces errors, especially when dealing with many digits.
-
Ease of Calculation: Multiplication and division become significantly simpler when numbers are in scientific notation. You can multiply or divide the coefficients and then add or subtract the exponents.
-
Standardisation: It provides a universally accepted format for representing numbers, facilitating communication across disciplines and geographical locations.
Applications of Scientific Notation Across Disciplines
Scientific notation's versatility shines across diverse fields:
-
Physics: Representing distances in astronomy (light-years), the size of atoms, or the strength of forces.
-
Chemistry: Expressing the mass of molecules or the concentration of solutions. Consider molarity calculations, where extremely small numbers are commonplace.
-
Biology: Describing the size of microorganisms or population sizes.
-
Computer Science: Representing memory capacity (gigabytes, terabytes), processing speeds, and data storage.
-
Finance: Dealing with large sums of money, national debts, or global economic indicators.
Further Exploration: Precision and Significant Figures
When working with scientific notation, understanding significant figures is vital. Significant figures indicate the precision of a measurement. In our example, 9.8 x 10<sup>-3</sup>, the number 9.8 has two significant figures. This means we're certain about the digits 9 and 8, but there's uncertainty in any further decimal places. The number of significant figures is crucial in determining the level of accuracy in calculations and reported results.
The rules for determining significant figures are as follows:
- All non-zero digits are significant.
- Zeros between non-zero digits are significant.
- Leading zeros (zeros to the left of the first non-zero digit) are not significant.
- Trailing zeros (zeros to the right of the last non-zero digit) are significant only if the number contains a decimal point.
Beyond 0.0098: Practicing with Different Numbers
To solidify your understanding, let's practice with a few more examples:
-
Convert 0.00000075 to scientific notation:
Move the decimal point seven places to the right to get 7.5. The exponent will be -7. Therefore, the scientific notation is 7.5 x 10<sup>-7</sup>.
-
Convert 45,600,000 to scientific notation:
Move the decimal point seven places to the left to get 4.56. The exponent will be 7. Therefore, the scientific notation is 4.56 x 10<sup>7</sup>. Note the inclusion of all significant figures here.
-
Convert 1.23 x 10<sup>5</sup> to standard decimal notation:
Move the decimal point five places to the right (because the exponent is positive). This gives 123,000.
-
Convert 8.7 x 10<sup>-2</sup> to standard decimal notation:
Move the decimal point two places to the left (because the exponent is negative). This gives 0.087.
Frequently Asked Questions (FAQ)
Q: What if the number is already between 1 and 10?
A: If a number is already between 1 and 10, it's already in scientific notation, with an exponent of 10<sup>0</sup> (which is 1). For example, 5 is the same as 5 x 10<sup>0</sup>.
Q: Can a number have more than one representation in scientific notation?
A: No. While you might move the decimal point differently, the correct scientific notation will always have a coefficient between 1 and 10. For instance, 98 x 10<sup>-4</sup> is not in correct scientific notation, even though it's numerically equal to 0.0098.
Q: Why is scientific notation important in calculations?
A: Scientific notation simplifies calculations involving very large or small numbers. It avoids writing out many zeros and makes multiplication and division easier by manipulating exponents and coefficients separately.
Conclusion
Mastering scientific notation is a fundamental skill in many scientific and technical fields. It provides a clear, concise, and efficient way to represent numbers across an enormous range of magnitudes. By understanding the steps involved in converting numbers to and from scientific notation and appreciating its underlying principles, you'll enhance your problem-solving capabilities and improve your understanding of numerical data in any context. This skill will prove invaluable as you continue your studies or work in any field that involves numerical analysis. Remember to always pay attention to significant figures to maintain accuracy in your work. Practice converting various numbers to and from scientific notation to solidify your understanding and build confidence in your abilities.
Latest Posts
Latest Posts
-
Cell Analogy Of A Car
Sep 04, 2025
-
Food Chain For Desert Ecosystem
Sep 04, 2025
-
Is Milk A Heterogeneous Mixture
Sep 04, 2025
-
Toys That Start With S
Sep 04, 2025
-
Is Soil A Biotic Factor
Sep 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 0.0098 In Scientific . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.