What Is 1/5 Of 2/3
salachar
Sep 08, 2025 · 5 min read
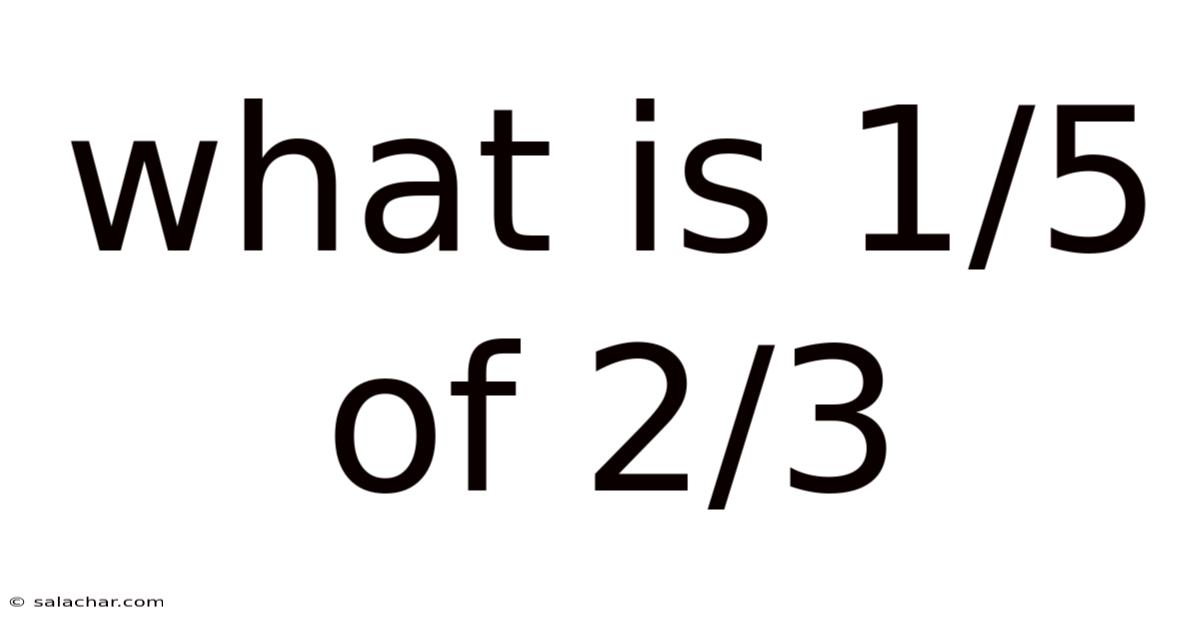
Table of Contents
What is 1/5 of 2/3? A Deep Dive into Fraction Multiplication
Finding a fraction of another fraction might seem daunting at first, but it's a fundamental concept in mathematics with wide-ranging applications. This article will guide you through the process of calculating 1/5 of 2/3, explaining the underlying principles in a clear and accessible way. We'll not only solve the problem but also explore the broader concepts of fraction multiplication and its relevance in various fields. By the end, you'll not only understand how to solve this specific problem but also have a solid grasp of the techniques involved.
Understanding Fractions: A Quick Recap
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) represents two equal parts making up the whole.
Multiplying Fractions: The Simple Rule
Multiplying fractions is surprisingly straightforward. The rule is simple: multiply the numerators together and multiply the denominators together. That's it!
Let's illustrate with a simple example: 1/2 x 1/3.
- Multiply the numerators: 1 x 1 = 1
- Multiply the denominators: 2 x 3 = 6
Therefore, 1/2 x 1/3 = 1/6.
Calculating 1/5 of 2/3: A Step-by-Step Guide
Now, let's tackle the problem at hand: finding 1/5 of 2/3. Remember, "of" in mathematics often signifies multiplication. Therefore, we can rewrite the problem as:
1/5 x 2/3
Following the rule for multiplying fractions:
- Multiply the numerators: 1 x 2 = 2
- Multiply the denominators: 5 x 3 = 15
This gives us the result: 2/15.
Therefore, 1/5 of 2/3 is 2/15.
Visualizing the Problem
Visual representations can often make abstract mathematical concepts easier to grasp. Imagine a rectangular pizza cut into 15 equal slices (representing the denominator of our final answer). If we take 2/3 of the pizza, that's 10 slices (2/3 x 15 = 10). Now, we want to find 1/5 of those 10 slices. Dividing the 10 slices into 5 equal groups gives us 2 slices per group. This visually confirms that 1/5 of 2/3 is indeed 2/15.
Simplifying Fractions: Finding the Lowest Terms
Sometimes, the result of fraction multiplication can be simplified. This means reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
In our case, 2/15 is already in its simplest form. The GCD of 2 and 15 is 1, and dividing both by 1 doesn't change the fraction's value. However, let's consider an example where simplification is necessary. If we had 4/8, the GCD of 4 and 8 is 4. Dividing both the numerator and denominator by 4 gives us 1/2, which is the simplified form.
The Importance of Understanding Fraction Multiplication
The ability to multiply fractions is crucial in many areas of life, not just in mathematics classes. Here are some examples:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Understanding fraction multiplication allows you to accurately scale recipes up or down. For instance, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you need to calculate 1/2 of 1/2, which is 1/4 cup of flour.
-
Construction and Engineering: Precise measurements are essential in construction and engineering. Fraction multiplication ensures accurate calculations of material quantities, dimensions, and proportions.
-
Finance and Budgeting: Managing finances often involves working with percentages and fractions. Understanding fraction multiplication helps in calculating discounts, interest rates, and proportions of budgets.
-
Data Analysis and Statistics: Many statistical calculations involve fractions and proportions. Understanding fraction multiplication is necessary for interpreting data and making informed decisions.
Beyond the Basics: More Complex Fraction Problems
While 1/5 of 2/3 is a relatively simple problem, the principles involved extend to more complex scenarios. For example, you might encounter problems involving mixed numbers (numbers with both whole and fractional parts) or more than two fractions. The fundamental process remains the same: convert mixed numbers to improper fractions (where the numerator is larger than the denominator), then multiply the numerators and the denominators separately, and finally, simplify the result if possible.
Frequently Asked Questions (FAQs)
Q: What if the fractions have different denominators?
A: You can still multiply them directly using the method described above. However, simplifying the result might be easier if you simplify the fractions before multiplying.
Q: Can I multiply fractions with whole numbers?
A: Yes! Think of the whole number as a fraction with a denominator of 1. For example, 2 x 1/3 is the same as 2/1 x 1/3 = 2/3.
Q: What about dividing fractions?
A: Dividing fractions involves multiplying the first fraction by the reciprocal (inverse) of the second fraction. The reciprocal of a fraction is obtained by switching the numerator and the denominator. For example, to divide 1/2 by 1/3, you would multiply 1/2 by 3/1 (the reciprocal of 1/3).
Conclusion: Mastering Fractions – A Stepping Stone to Success
Calculating 1/5 of 2/3, as we've seen, is a relatively straightforward application of fraction multiplication. However, understanding the underlying principles is crucial for tackling more complex mathematical problems and for applying these concepts in various real-world scenarios. Mastering fraction multiplication lays a strong foundation for further mathematical learning and enhances your ability to solve problems across diverse fields. Remember the simple rule: multiply the numerators, multiply the denominators, and simplify if possible. With practice and a clear understanding of the concepts, you'll confidently navigate the world of fractions and their applications.
Latest Posts
Latest Posts
-
Shiba Inu Black Lab Mix
Sep 09, 2025
-
What Is A Template Strand
Sep 09, 2025
-
Electron Dot Diagram For Beryllium
Sep 09, 2025
-
Henrys Law Vs Raoults Law
Sep 09, 2025
-
Final Goods Vs Intermediate Goods
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/5 Of 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.