What Is 1/5 Of 20
salachar
Sep 12, 2025 · 5 min read
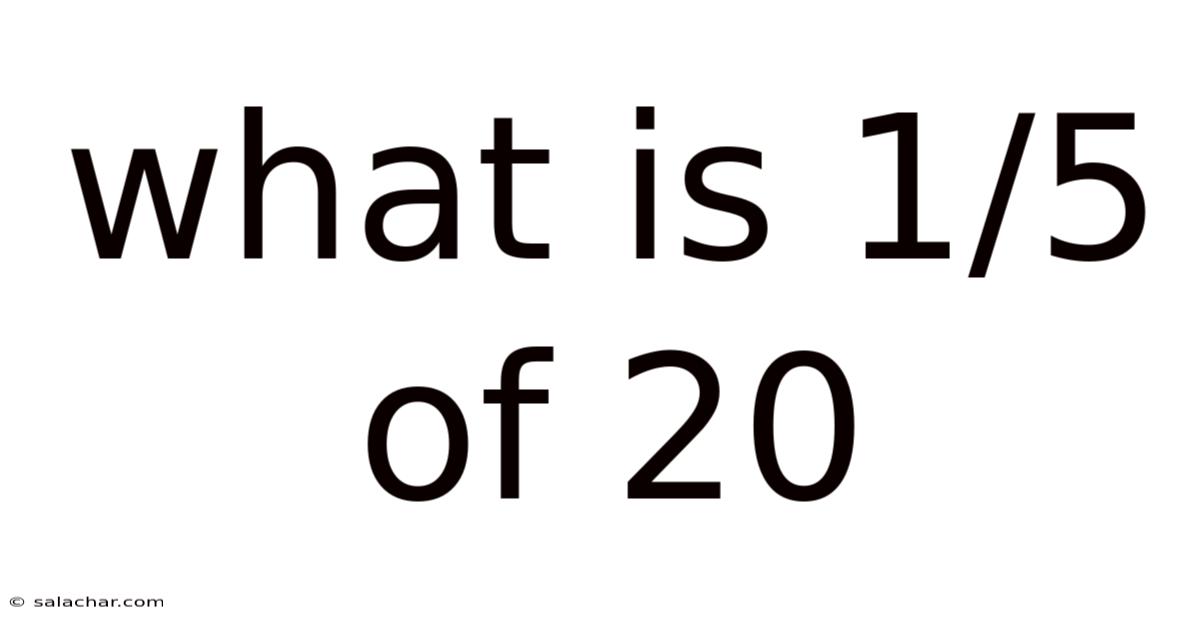
Table of Contents
What is 1/5 of 20? A Deep Dive into Fractions and Their Applications
Finding 1/5 of 20 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation opens the door to a broader comprehension of fractions, their practical applications in everyday life, and even their importance in more advanced mathematical concepts. This article will not only answer the question "What is 1/5 of 20?" but will also delve into the underlying principles, explore various methods of solving similar problems, and discuss the relevance of fractions in diverse fields.
Understanding Fractions: The Building Blocks
Before we tackle the specific problem, let's establish a firm grasp of what fractions represent. A fraction, at its core, is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
In the fraction 1/5, the denominator (5) tells us that the whole is divided into five equal parts. The numerator (1) signifies that we are interested in only one of those five parts. Therefore, 1/5 represents one-fifth of a whole.
Calculating 1/5 of 20: Multiple Approaches
Now, let's address the central question: What is 1/5 of 20? There are several ways to solve this:
1. Division Method:
This is the most straightforward approach. To find 1/5 of 20, we simply divide 20 by the denominator, 5:
20 ÷ 5 = 4
Therefore, 1/5 of 20 is 4.
2. Multiplication Method:
We can also solve this using multiplication. Remember that "of" in mathematics often signifies multiplication. So, finding 1/5 of 20 can be expressed as:
(1/5) × 20
To multiply a fraction by a whole number, we multiply the numerator by the whole number and keep the denominator the same:
(1 × 20) / 5 = 20/5
Then, we simplify the fraction by dividing the numerator by the denominator:
20 ÷ 5 = 4
Again, we arrive at the answer: 1/5 of 20 is 4.
3. Visual Representation:
Imagine you have 20 apples. To find 1/5 of them, divide the apples into 5 equal groups. Each group will contain:
20 ÷ 5 = 4 apples
This visual method reinforces the understanding of what a fraction represents and how it relates to a whole.
Expanding the Concept: Fractions Beyond Simple Calculations
While finding 1/5 of 20 is a basic exercise, the underlying principles are crucial for understanding more complex fractional calculations. Let's explore some related concepts:
-
Finding a Fraction of a Fraction: Suppose we need to find 1/3 of 1/5 of 20. We would first calculate 1/5 of 20 (which is 4), and then find 1/3 of 4:
(1/3) × 4 = 4/3 = 1 and 1/3
-
Finding Multiple Fractions of a Number: If we want to find 2/5 of 20, we would multiply 20 by the fraction 2/5:
(2/5) × 20 = (2 × 20) / 5 = 40/5 = 8
-
Working with Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 2 1/2). To find a fraction of a mixed number, it's often easier to convert the mixed number into an improper fraction first (where the numerator is larger than the denominator). For instance, to find 1/5 of 2 1/2, we would first convert 2 1/2 to 5/2:
(1/5) × (5/2) = 5/10 = 1/2
Real-World Applications of Fractions
Fractions are not confined to the classroom; they are integral to many aspects of daily life:
-
Cooking and Baking: Recipes frequently use fractions (e.g., 1/2 cup of flour, 1/4 teaspoon of salt). Accurate measurement is crucial for successful results.
-
Shopping and Budgeting: Discounts are often expressed as fractions (e.g., 1/3 off). Understanding fractions helps consumers calculate the final price and make informed purchasing decisions.
-
Measurement and Construction: Carpenters, engineers, and other professionals rely on fractions for precise measurements and calculations.
-
Data Analysis and Statistics: Fractions are used extensively in representing proportions, probabilities, and statistical data.
Fractions in Advanced Mathematics
The fundamental understanding of fractions is a stepping stone to more advanced mathematical concepts:
-
Algebra: Solving algebraic equations often involves working with fractions and manipulating them to isolate variables.
-
Calculus: Derivatives and integrals, core concepts in calculus, frequently involve fractional expressions.
-
Probability and Statistics: Fractions are essential in expressing probabilities and relative frequencies in statistical analysis.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of a fraction?
A: The simplest form of a fraction is when the numerator and denominator have no common factors other than 1. For instance, 2/4 simplifies to 1/2 because both 2 and 4 are divisible by 2.
Q: How do I add or subtract fractions?
A: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions accordingly. Then, you add or subtract the numerators and keep the common denominator.
Q: How do I multiply fractions?
A: To multiply fractions, simply multiply the numerators together and the denominators together. Then, simplify the resulting fraction if possible.
Q: How do I divide fractions?
A: To divide fractions, invert (flip) the second fraction (the divisor) and multiply it by the first fraction (the dividend).
Conclusion: The Significance of a Simple Fraction
While initially appearing trivial, the question "What is 1/5 of 20?" reveals a wealth of knowledge about fractions and their profound impact on various aspects of mathematics and everyday life. Mastering fractional calculations lays a solid foundation for tackling more complex mathematical problems and fosters a deeper understanding of numerical relationships in the world around us. The ability to accurately and efficiently work with fractions is a valuable skill that extends far beyond the classroom, contributing significantly to success in various academic and professional pursuits. So, remember that the seemingly simple task of finding 1/5 of 20 unlocks a world of mathematical possibilities.
Latest Posts
Latest Posts
-
185 Lbs Convert To Kg
Sep 12, 2025
-
The Near Point Of Accommodation
Sep 12, 2025
-
School Of Whales Nyt Crossword
Sep 12, 2025
-
Is Salt Water A Mixture
Sep 12, 2025
-
Negative Times A Negative Rules
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/5 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.