What Is 15 Of $15
salachar
Sep 13, 2025 · 5 min read
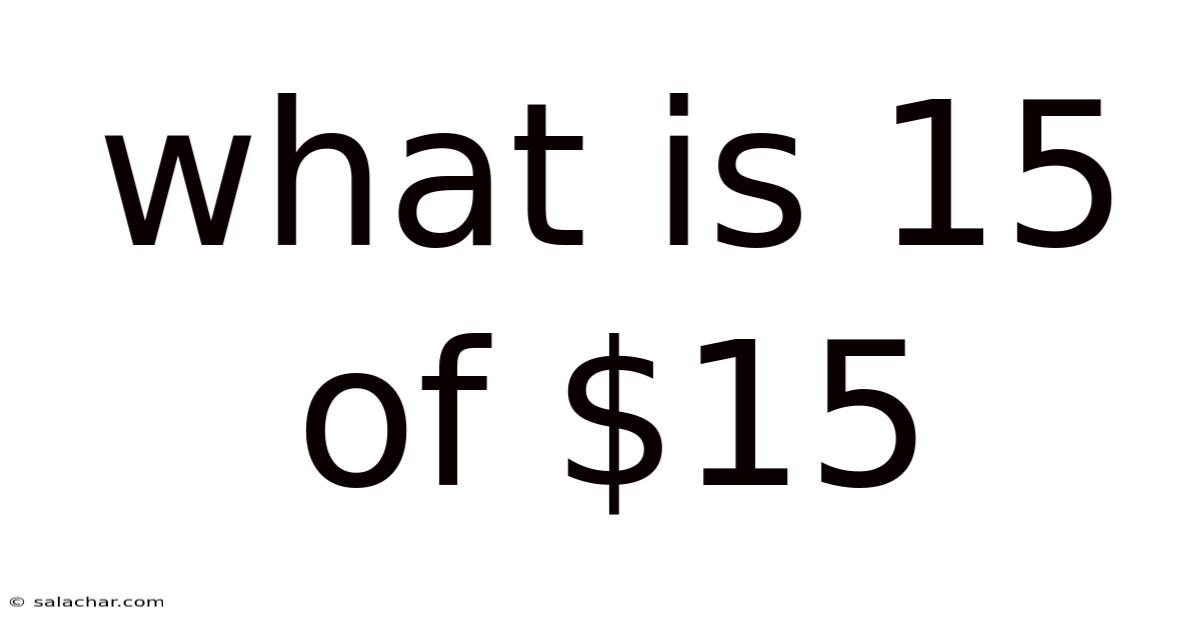
Table of Contents
What is 15% of $15? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in everyday life, from calculating sales tax and discounts to analyzing financial statements and understanding statistical data. This article will not only answer the question, "What is 15% of $15?" but will also provide a comprehensive guide to calculating percentages, exploring different methods, and showcasing their practical applications. We'll delve into the underlying mathematical principles and offer clear, step-by-step examples to solidify your understanding. By the end, you'll be confident in calculating percentages and applying this crucial skill in various real-world scenarios.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 15% means 15 out of 100, or 15/100, which simplifies to 3/20 as a fraction. Understanding this fundamental concept is crucial for calculating percentages accurately.
Calculating 15% of $15: Three Different Methods
There are several ways to calculate 15% of $15. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. To calculate a percentage of a number, we first convert the percentage into its decimal equivalent. To do this, we divide the percentage by 100. In this case:
15% ÷ 100 = 0.15
Next, we multiply this decimal by the number we want to find the percentage of:
0.15 x $15 = $2.25
Therefore, 15% of $15 is $2.25.
Method 2: Using Fractions
As mentioned earlier, 15% can be expressed as the fraction 15/100, which simplifies to 3/20. We can then use this fraction to calculate 15% of $15:
(3/20) x $15 = $45/20 = $2.25
This method confirms our previous result: 15% of $15 is $2.25.
Method 3: Using Proportions
This method is particularly helpful for understanding the underlying relationship between the percentage and the whole. We can set up a proportion:
15/100 = x/$15
Where 'x' represents the value we want to find (15% of $15). To solve for 'x', we cross-multiply:
100x = 15 x $15
100x = $225
x = $225 / 100
x = $2.25
Once again, we find that 15% of $15 is $2.25.
Beyond the Calculation: Practical Applications of Percentages
While calculating 15% of $15 might seem like a simple exercise, understanding percentage calculations is crucial in numerous real-world situations. Here are some examples:
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages. Understanding percentages helps you quickly calculate the final price after a discount. For instance, a 20% discount on a $50 item means you'll save 20% of $50, which is $10, making the final price $40.
-
Taxes: Sales tax, income tax, and other taxes are usually expressed as percentages. Calculating the tax amount requires understanding percentage calculations. If the sales tax is 6%, you would calculate 6% of the item's price to determine the tax amount.
-
Tips and Gratuities: When dining out, it’s customary to leave a tip, often expressed as a percentage of the bill. Calculating a 15% or 20% tip accurately requires proficiency in percentage calculations.
-
Financial Statements: Financial statements like balance sheets and income statements often use percentages to represent various financial ratios and trends. Understanding these percentages is crucial for financial analysis and decision-making.
-
Statistics and Data Analysis: Percentages are widely used in statistics to represent proportions, probabilities, and changes over time. For example, unemployment rates, population growth rates, and survey results are often expressed as percentages.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding how to calculate interest is essential for making informed financial decisions.
Expanding Your Percentage Skills: More Complex Scenarios
While calculating 15% of $15 is relatively straightforward, many real-world scenarios involve more complex percentage calculations. Let's consider some examples:
- Calculating the Original Price after a Discount: If an item is on sale for $30 after a 25% discount, how much was the original price? This requires working backward from the discounted price. Let 'x' represent the original price:
x - 0.25x = $30
0.75x = $30
x = $30 / 0.75
x = $40
The original price was $40.
- Calculating Percentage Increase or Decrease: If a value increases from 100 to 120, the percentage increase is calculated as follows:
((120 - 100) / 100) x 100% = 20%
The value increased by 20%. Conversely, if a value decreases from 100 to 80, the percentage decrease is 20%.
-
Compound Interest: Compound interest is calculated on both the principal amount and accumulated interest. This requires repeated percentage calculations over time. Understanding compound interest is vital for long-term financial planning.
-
Percentage Points vs. Percentages: It's important to distinguish between percentage points and percentages. A change from 10% to 15% is a 5-percentage-point increase, but a 50% increase in the percentage itself.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include:
- Incorrectly converting percentages to decimals.
- Confusing percentage points with percentages.
- Not understanding the context of the problem.
- Rounding errors in intermediate calculations.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, many online calculators are readily available that can quickly calculate percentages. However, understanding the underlying principles is crucial for solving complex problems and applying percentage calculations in various contexts.
Q: How can I improve my skills in calculating percentages?
A: Practice is key! Solve various percentage problems, starting with simpler examples and gradually increasing the complexity. Use different methods to reinforce your understanding. Review the fundamentals, ensuring a strong grasp of fractions, decimals, and ratios.
Conclusion
Understanding percentages is a vital life skill applicable across many areas. While seemingly simple, the ability to accurately calculate and interpret percentages is essential for financial literacy, data analysis, and everyday decision-making. This article has not only answered the specific question of "What is 15% of $15?" but also provided a comprehensive guide to calculating percentages using different methods and exploring numerous practical applications. By mastering percentage calculations, you equip yourself with a powerful tool for navigating the quantitative aspects of modern life, empowering you to make informed decisions and confidently tackle various numerical challenges. Remember to practice regularly and apply your knowledge in different contexts to solidify your understanding and build your confidence.
Latest Posts
Latest Posts
-
Example Of A Mechanical Energy
Sep 13, 2025
-
Is Solubility A Physical Property
Sep 13, 2025
-
Difference Between Amplitude And Frequency
Sep 13, 2025
-
How Tall Was A Brontosaurus
Sep 13, 2025
-
How To Draw A Chromosome
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of $15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.