What Is 15 Of 275
salachar
Sep 09, 2025 · 5 min read
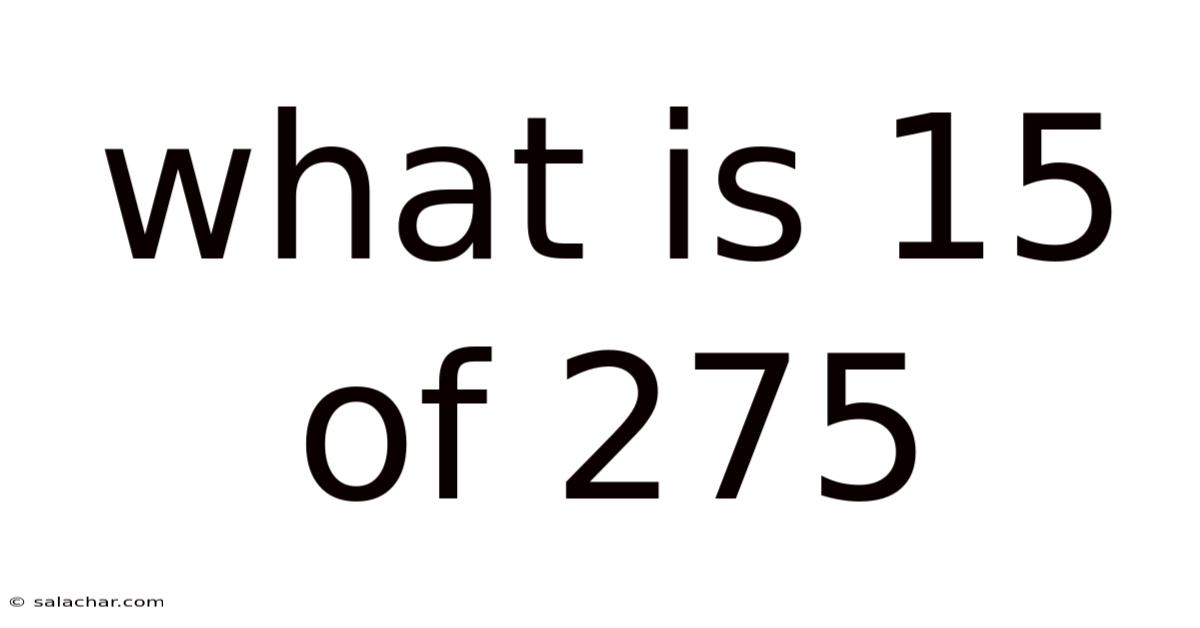
Table of Contents
What is 15% of 275? A Deep Dive into Percentages and Their Applications
Finding 15% of 275 might seem like a simple arithmetic problem, but it opens a door to a wider understanding of percentages, their practical applications, and the different methods used to calculate them. This article will not only show you how to calculate 15% of 275 but also explore the underlying concepts, offer alternative calculation methods, and delve into real-world examples where understanding percentages is crucial.
Introduction: Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 15% means 15 out of 100, or 15/100, which can be simplified to 3/20 as a fraction. Understanding this fundamental concept is crucial for calculating percentages efficiently.
Method 1: Using Decimal Conversion
The most straightforward way to calculate 15% of 275 is to convert the percentage to its decimal equivalent. To do this, divide the percentage by 100:
15% ÷ 100 = 0.15
Now, multiply this decimal by the number you want to find the percentage of:
0.15 x 275 = 41.25
Therefore, 15% of 275 is 41.25.
Method 2: Using Fractions
As mentioned earlier, 15% can be expressed as the fraction 15/100 or its simplified form, 3/20. Using this fractional representation, we can calculate 15% of 275 as follows:
(3/20) x 275 = 825/20 = 41.25
This method demonstrates the equivalence between percentages, decimals, and fractions, reinforcing the underlying mathematical principles.
Method 3: Proportion Method
This method uses the concept of proportion to solve the problem. We can set up a proportion:
15/100 = x/275
Where 'x' represents the value we want to find (15% of 275). To solve for 'x', we cross-multiply:
15 x 275 = 100x
4125 = 100x
x = 4125/100 = 41.25
This method highlights the relationship between the percentage, the whole amount, and the part we are trying to determine.
Method 4: Using a Calculator
Most calculators have a percentage function (%) which simplifies the process. Simply enter 275, press the multiplication key (x), then enter 15, and finally press the percentage key (%). The calculator will automatically perform the calculation and display the result: 41.25. This is the quickest method for practical applications.
Real-World Applications of Percentage Calculations:
Understanding percentage calculations is essential in various aspects of daily life and professional fields. Here are a few examples:
-
Sales Tax: Calculating the sales tax on a purchase involves finding a percentage of the original price. For instance, if the sales tax is 6%, and you buy an item for $100, you'll pay an additional $6 in tax (6% of $100).
-
Discounts: Retail stores frequently offer discounts as a percentage off the original price. If a store offers a 20% discount on a $50 item, you'll save $10 (20% of $50).
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages helps in evaluating the financial implications of borrowing or saving money.
-
Tips and Gratuities: Calculating tips in restaurants or service charges often involves determining a percentage of the total bill.
-
Grade Calculations: In education, grades are often expressed as percentages reflecting the proportion of correct answers or successful completion of assignments.
-
Statistical Analysis: Percentages are extensively used in statistical analysis to represent proportions, frequencies, and probabilities. They are crucial in surveys, market research, and scientific studies.
-
Financial Statements: Financial statements, such as balance sheets and income statements, rely heavily on percentages to illustrate ratios and trends. For instance, the profit margin is expressed as a percentage of revenue.
-
Growth Rates: Percentages are instrumental in tracking growth rates in various areas, including population growth, economic growth, and investment returns.
Advanced Percentage Concepts:
While finding 15% of 275 is a relatively simple calculation, understanding percentages involves more complex scenarios:
-
Calculating the Percentage Increase or Decrease: Determining the percentage change between two values requires calculating the difference between the values, dividing it by the original value, and then multiplying by 100. For example, if a value increases from 100 to 120, the percentage increase is [(120-100)/100] x 100 = 20%.
-
Finding the Original Value: If you know the percentage and the resulting value, you can work backward to find the original value. For instance, if 20% of a value is 40, then the original value is 40 / (20/100) = 200.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Compound interest calculations utilize percentages repeatedly over time, making them more complex.
-
Percentage Points vs. Percentage Change: These terms are often confused. A change of 5 percentage points is different from a 5% increase. For example, a change from 10% to 15% is a 5 percentage point increase but a 50% increase in the percentage itself.
Frequently Asked Questions (FAQ):
-
Q: What if I need to find a different percentage of 275?
A: You can use any of the methods described above, simply substituting the desired percentage for 15%.
-
Q: Are there any online calculators for percentage calculations?
A: Yes, numerous online calculators are available that can easily compute percentages.
-
Q: How can I improve my understanding of percentages?
A: Practice regularly with various problems, focusing on the underlying concepts rather than just memorizing formulas. Work through examples involving different scenarios and gradually tackle more complex problems.
-
Q: Why are percentages important to learn?
A: Percentages are fundamental to everyday life, enabling us to understand and analyze various aspects of finance, statistics, and various other fields. Understanding percentages empowers you to make informed decisions in numerous situations.
Conclusion:
Calculating 15% of 275, as demonstrated above, is a simple yet illustrative example of the broader application of percentage calculations. Mastering this fundamental skill is vital for navigating various aspects of life, from managing personal finances to understanding statistical data and professional contexts. By understanding the different methods and exploring the diverse applications, you can confidently tackle any percentage-related problem and enhance your overall mathematical comprehension. Remember to practice regularly and explore the different methods to solidify your understanding. The more you engage with these concepts, the easier they will become, empowering you to tackle more complex percentage-based problems with ease and confidence.
Latest Posts
Latest Posts
-
Are Stars Bigger Than Earth
Sep 09, 2025
-
Fox In The Hen House
Sep 09, 2025
-
Is In Front A Preposition
Sep 09, 2025
-
Summary Of The Book Heidi
Sep 09, 2025
-
Is Caco3 Ionic Or Covalent
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 275 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.