What Is 15 Of 480
salachar
Sep 14, 2025 · 5 min read
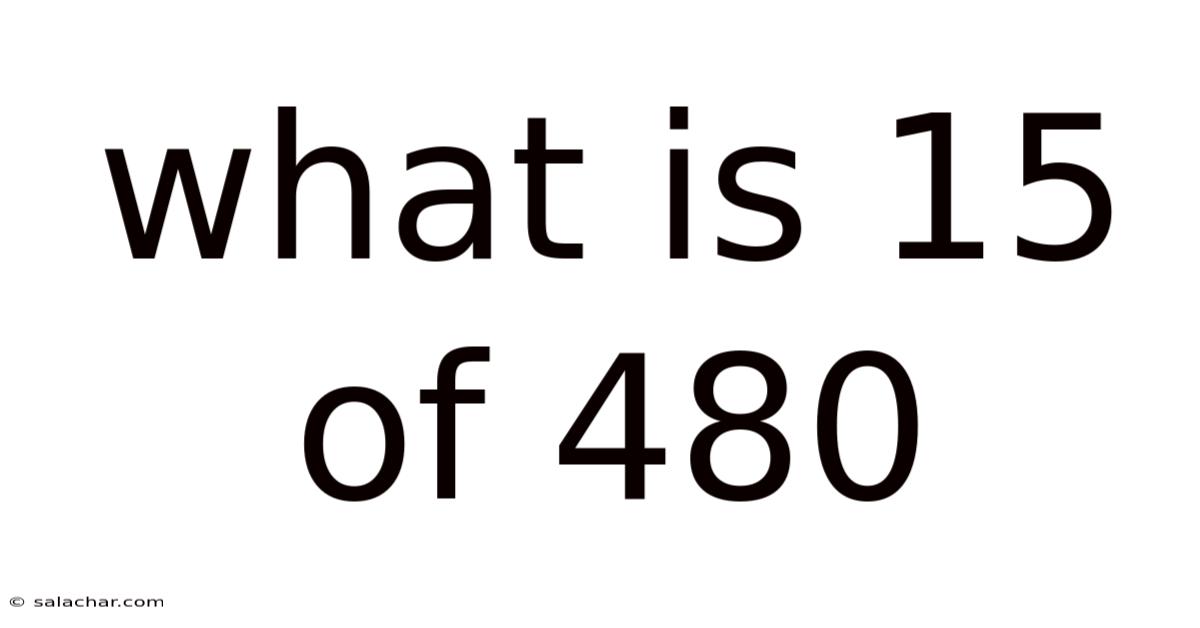
Table of Contents
What is 15% of 480? A Comprehensive Guide to Percentages and Their Applications
Finding 15% of 480 might seem like a simple arithmetic problem, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide will not only answer the question "What is 15% of 480?" but also delve into the methods for calculating percentages, explain the concept in detail, and explore its real-world relevance.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (Latin: per centum). For example, 15% means 15 out of 100, or 15/100, which is equivalent to the decimal 0.15. Percentages are used extensively to represent proportions, ratios, and changes in values. They provide a standardized way to compare different quantities, making them easier to understand and interpret.
Methods for Calculating 15% of 480
There are several ways to calculate 15% of 480. Let's explore the most common approaches:
1. Using the Decimal Equivalent:
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent by dividing by 100. 15% becomes 0.15. Then, we multiply this decimal by the number we're finding the percentage of:
480 * 0.15 = 72
Therefore, 15% of 480 is 72.
2. Using Fraction Conversion:
We can also convert the percentage to a fraction. 15% is equivalent to 15/100. Simplifying this fraction, we get 3/20. Then, we multiply this fraction by 480:
(3/20) * 480 = 3 * (480/20) = 3 * 24 = 72
Again, 15% of 480 is 72.
3. Using Proportions:
This method utilizes the concept of ratios. We can set up a proportion:
15/100 = x/480
where 'x' represents 15% of 480. To solve for 'x', we cross-multiply:
100x = 15 * 480
100x = 7200
x = 7200/100
x = 72
This confirms that 15% of 480 is 72.
Real-World Applications of Percentage Calculations
The ability to calculate percentages efficiently is crucial in various aspects of daily life and professional settings. Here are some examples:
-
Retail Discounts: Sales and discounts are frequently expressed as percentages. Understanding percentage calculations allows you to quickly determine the actual price after a discount. For instance, a 15% discount on a $480 item would result in a savings of $72, bringing the final price down to $408.
-
Taxes and Tax Rates: Sales tax, income tax, and other taxes are often calculated as a percentage of the total amount. Knowing how to calculate percentages helps in determining the exact tax amount and the final price inclusive of tax.
-
Interest Rates: Interest rates on loans, mortgages, and savings accounts are expressed as percentages. Calculating percentages is essential for understanding the total interest payable or earned over a specific period.
-
Financial Statements: Financial statements like balance sheets and income statements often utilize percentages to represent key financial ratios and metrics. This allows for easier comparison of financial performance across different periods or companies.
-
Statistical Analysis: Percentages are fundamental in statistical analysis. They are used to represent proportions, probabilities, and changes in data, facilitating the interpretation and visualization of complex datasets.
-
Tip Calculation: Calculating a tip in a restaurant typically involves determining a percentage of the total bill. For example, a 15% tip on a $480 bill would be $72.
-
Grade Calculation: In many educational systems, final grades are often calculated as a weighted average of different assessment components, with each component carrying a specific percentage.
-
Commission Calculation: Salespeople and agents often earn a commission based on a percentage of their sales. Understanding percentage calculations is essential for tracking earnings and setting sales targets.
Expanding on Percentage Concepts: Beyond the Basics
While calculating 15% of 480 is relatively simple, the underlying principles of percentages can be applied to more complex scenarios.
-
Calculating the Percentage Increase or Decrease: To determine the percentage change between two values, you first find the difference between the values, then divide by the original value, and finally multiply by 100%. For instance, if a value increases from 400 to 480, the percentage increase is [(480-400)/400] * 100% = 20%.
-
Finding the Original Value: If you know the percentage and the resulting value, you can work backward to find the original value. For example, if 15% of a number is 72, the original number is 72 / 0.15 = 480.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This requires repeated percentage calculations over time.
Frequently Asked Questions (FAQ)
Q1: How can I calculate percentages quickly without a calculator?
A1: For simpler percentages like 10%, 20%, 50%, etc., you can use mental math. For example, 10% of 480 is simply 48. You can then use this to derive other percentages. For instance, 5% would be half of 10% (24), and 15% would be 10% + 5% (48 + 24 = 72).
Q2: Are there any online tools or calculators for percentage calculations?
A2: Yes, many online calculators are available that can perform percentage calculations. Simply search for "percentage calculator" on the internet.
Q3: What if I need to calculate a more complex percentage, such as 17.5% of 480?
A3: You can use the same methods described earlier – decimal conversion, fraction conversion, or proportions – adapting them to the specific percentage you are working with.
Conclusion
Calculating 15% of 480, resulting in 72, is a straightforward application of percentage calculations. However, understanding the broader concepts of percentages and their various methods of calculation is crucial for navigating numerous situations in everyday life and various professional fields. Mastering this skill empowers you to analyze data, understand financial reports, make informed decisions, and solve various problems involving proportions and ratios. The applications extend beyond simple arithmetic problems, touching upon finance, statistics, and various other disciplines. The ability to confidently tackle percentage calculations lays a strong foundation for more advanced mathematical concepts and real-world problem-solving.
Latest Posts
Latest Posts
-
Different Types Of Electrical Cables
Sep 14, 2025
-
The Parts Of A Plant
Sep 14, 2025
-
How Does Amoeba Acquire Food
Sep 14, 2025
-
What Cell Has More Mitochondria
Sep 14, 2025
-
Can Transformers Work With Dc
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 480 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.