What Is 20 Of $3000
salachar
Sep 12, 2025 · 5 min read
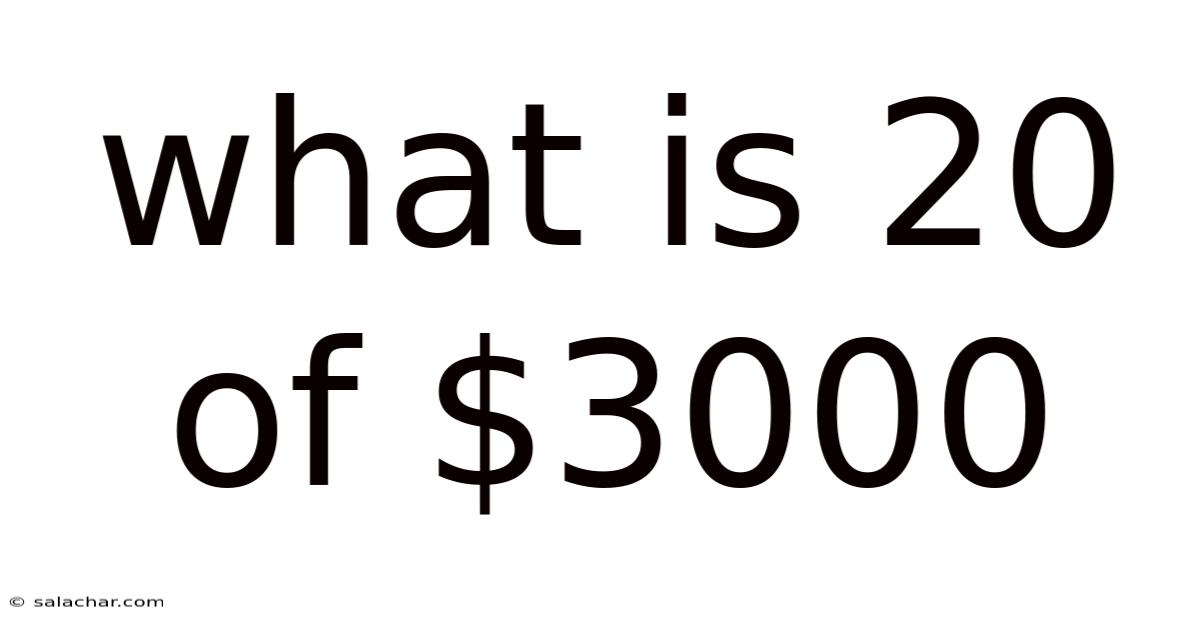
Table of Contents
What is 20% of $3000? A Comprehensive Guide to Percentage Calculations
Finding 20% of $3000 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various applications in everyday life, from calculating discounts and taxes to understanding financial statements and data analysis. This comprehensive guide will not only answer the initial question but also equip you with the skills to tackle similar percentage problems confidently. We'll explore different methods, delve into the mathematical concepts, and even touch upon real-world applications to solidify your understanding.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 20% means 20 out of 100, which can be written as the fraction 20/100 or the decimal 0.20. This fundamental understanding is key to solving any percentage problem.
Method 1: Using Decimal Multiplication
This is arguably the most straightforward method for calculating percentages. We convert the percentage to its decimal equivalent and then multiply it by the total value.
Steps:
-
Convert the percentage to a decimal: To convert 20% to a decimal, divide it by 100: 20% ÷ 100 = 0.20.
-
Multiply the decimal by the total value: Multiply 0.20 by $3000: 0.20 x $3000 = $600.
Therefore, 20% of $3000 is $\boxed{$600}$.
Method 2: Using Fraction Multiplication
This method involves converting the percentage to a fraction and then multiplying it by the total value.
Steps:
-
Convert the percentage to a fraction: 20% can be written as the fraction 20/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 20: 20/100 = 1/5.
-
Multiply the fraction by the total value: Multiply 1/5 by $3000: (1/5) x $3000 = $600.
Again, we arrive at the answer: 20% of $3000 is $\boxed{$600}$.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where one ratio represents the percentage and the other represents the unknown value.
Steps:
-
Set up a proportion: We can set up the proportion: 20/100 = x/$3000, where 'x' represents the unknown value (20% of $3000).
-
Cross-multiply: Cross-multiplying gives us: 100x = 20 x $3000.
-
Solve for x: Divide both sides by 100: x = (20 x $3000) / 100 = $600.
Once again, the solution is $\boxed{$600}$.
Real-World Applications: Beyond the Textbook
Understanding percentage calculations has numerous practical applications in various aspects of life:
-
Shopping Discounts: Imagine a store offering a 20% discount on a $3000 item. Using the methods discussed above, you'd quickly calculate the discount as $600, resulting in a final price of $2400.
-
Taxes: Calculating sales tax or income tax often involves percentage calculations. If the sales tax in your area is 6%, you'd multiply the price of an item by 0.06 to determine the tax amount.
-
Investment Returns: Investors frequently use percentages to track investment returns. A 10% return on a $10,000 investment means an increase of $1000.
-
Financial Statements: Analyzing financial statements requires a strong understanding of percentages. Profit margins, debt-to-equity ratios, and many other key financial metrics are expressed as percentages.
-
Data Analysis: Percentages are essential in data analysis for comparing proportions, tracking trends, and making informed decisions based on statistical data. For example, understanding the percentage of customers who responded positively to a survey can inform business strategies.
Beyond 20% of $3000: Generalizing the Process
The methods described above can be applied to calculate any percentage of any number. Simply replace the percentage and the total value with the desired values and follow the steps. For instance, to find 15% of $2500:
-
Decimal Method: 0.15 x $2500 = $375
-
Fraction Method: (15/100) x $2500 = $375 (simplified fraction: 3/20)
-
Proportion Method: 15/100 = x/$2500 => x = $375
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage increase or decrease?
A: To calculate a percentage increase, first find the difference between the new value and the original value. Then, divide this difference by the original value and multiply by 100 to express it as a percentage. For a percentage decrease, the process is similar, but the result will be negative.
Q: Are there any online calculators or software that can help with percentage calculations?
A: Yes, many online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) offer built-in functions for calculating percentages. These tools can be helpful for complex calculations or when dealing with large datasets.
Q: How can I improve my understanding of percentages?
A: Practice is key! Try solving various percentage problems with different numbers and scenarios. You can also find numerous online resources, tutorials, and practice exercises to help you improve your skills. Understanding the underlying concepts of fractions and decimals is also crucial.
Q: What are some common mistakes to avoid when calculating percentages?
A: Common mistakes include incorrect decimal conversion, errors in multiplication or division, and forgetting to express the result as a percentage. Always double-check your calculations and ensure you're using the correct values.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a fundamental skill with wide-ranging applications. This guide has demonstrated three reliable methods – using decimal multiplication, fraction multiplication, and the proportion method – for solving percentage problems. By mastering these methods and understanding the underlying concepts, you'll be well-equipped to tackle various percentage calculations in your personal and professional life. Remember, practice makes perfect. The more you work with percentages, the more comfortable and confident you'll become. So, grab a calculator, a few practice problems, and start honing your skills today! You'll find that the ability to calculate percentages quickly and accurately becomes an invaluable tool in many aspects of life.
Latest Posts
Latest Posts
-
Sho Full Form In Police
Sep 12, 2025
-
1 20 On The Periodic Table
Sep 12, 2025
-
How Is Paper Used Today
Sep 12, 2025
-
Units For Spring Constant K
Sep 12, 2025
-
Lab Equipment Names And Uses
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of $3000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.