What Is 25 Of 22
salachar
Sep 14, 2025 · 5 min read
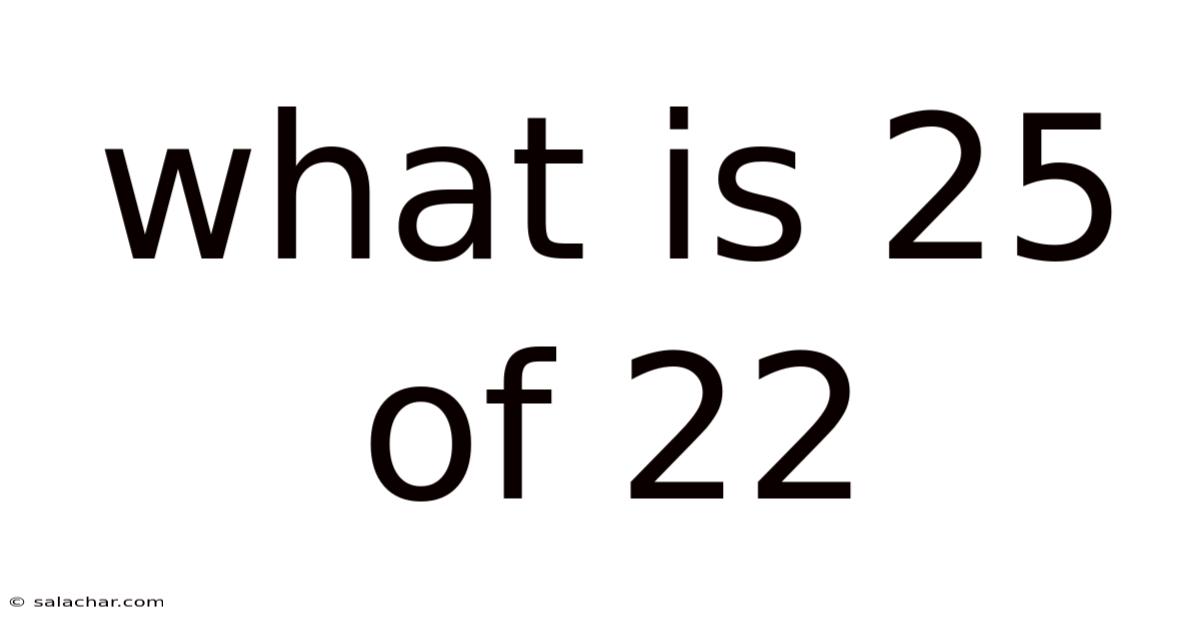
Table of Contents
What is 25% of 22? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding financial statements and statistical data. This article will not only answer the question "What is 25% of 22?" but will also delve into the underlying concepts of percentages, providing you with a comprehensive understanding and equipping you with the tools to solve similar problems independently.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (from the Latin per centum). Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Percentages are used to represent proportions or ratios, making it easier to compare different quantities or to express parts of a whole. They are ubiquitous in various fields, including finance, statistics, science, and everyday life.
Calculating 25% of 22: The Step-by-Step Approach
There are several ways to calculate 25% of 22. Let's explore the most common methods:
Method 1: Using Fractions
As mentioned earlier, 25% is equivalent to 1/4. Therefore, finding 25% of 22 is the same as finding 1/4 of 22. To do this, we simply divide 22 by 4:
22 ÷ 4 = 5.5
Therefore, 25% of 22 is 5.5.
Method 2: Using Decimal Equivalents
Percentages can also be expressed as decimals. To convert a percentage to a decimal, divide the percentage by 100. For 25%, this would be:
25 ÷ 100 = 0.25
Now, to find 25% of 22, we multiply 22 by 0.25:
22 x 0.25 = 5.5
Again, we arrive at the answer: 25% of 22 is 5.5.
Method 3: Using Proportions
We can also solve this problem using proportions. We can set up a proportion:
25/100 = x/22
Where 'x' represents the value we want to find (25% of 22). To solve for 'x', we cross-multiply:
25 x 22 = 100x
550 = 100x
x = 550 ÷ 100
x = 5.5
Therefore, 25% of 22 is 5.5.
Explanation of the Mathematical Principles
The methods above demonstrate different approaches to solving percentage problems, all based on the fundamental principle that a percentage represents a fraction of 100. The key mathematical operations involved are division and multiplication. The choice of method often depends on personal preference and the complexity of the problem. For simple percentages like 25%, the fraction method is often the quickest and easiest. For more complex percentages, the decimal method or proportions might be more efficient.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
- Sales and Discounts: Retail stores frequently offer discounts expressed as percentages. For example, a 25% discount on a $22 item would mean a reduction of $5.50 (25% of $22).
- Taxes: Sales tax and other taxes are often calculated as a percentage of the purchase price or income.
- Tips: Calculating a tip in a restaurant usually involves determining a percentage of the total bill.
- Financial Statements: Financial statements like income statements and balance sheets utilize percentages extensively to show proportions of different revenue streams, expenses, assets, and liabilities.
- Statistical Analysis: Percentages are fundamental in statistical analysis to represent proportions within datasets, allowing for meaningful comparisons and interpretations.
- Scientific Measurements and Experiments: In scientific research, percentages are used to represent concentrations, yields, and error margins.
- Everyday Life: Percentages are used constantly in everyday life to understand proportions, discounts, and various ratios.
Frequently Asked Questions (FAQs)
Q1: How do I calculate a different percentage of a number?
A1: Follow the same methods outlined above, but substitute the desired percentage for 25%. For example, to find 15% of 22, you would either divide 22 by 100/15 (or multiply 22 by 0.15).
Q2: What if the percentage is a decimal, like 22.5%?
A2: You can still use the same methods. Convert the decimal percentage to a decimal (22.5% = 0.225) and multiply by the number (22 x 0.225 = 4.95).
Q3: How can I improve my understanding of percentages?
A3: Practice regularly! Work through various percentage problems with different numbers and percentages. Use online calculators or worksheets to check your work and identify areas where you need more practice. Familiarize yourself with different calculation methods to find the approach that works best for you.
Q4: Are there any online tools to help calculate percentages?
A4: Yes, many online percentage calculators are available. These tools can be helpful for checking your work or for solving more complex percentage problems.
Advanced Concepts: Percentage Increase and Decrease
Beyond simple percentage calculations, understanding percentage increases and decreases is essential in many applications.
- Percentage Increase: This calculates the percentage change when a value increases. The formula is: [(New Value - Original Value) / Original Value] x 100%.
- Percentage Decrease: This calculates the percentage change when a value decreases. The formula is: [(Original Value - New Value) / Original Value] x 100%.
Conclusion: Mastering Percentages for Real-World Success
Calculating percentages, as demonstrated by finding 25% of 22, is a fundamental mathematical skill with widespread applicability. The ability to accurately and efficiently calculate percentages is crucial for success in various fields and in navigating everyday life. By understanding the underlying principles and practicing different methods, you can confidently tackle percentage problems and leverage this skill to make informed decisions in various contexts. Remember, practice makes perfect, so keep practicing until you feel comfortable and confident in your ability to work with percentages. This foundation in percentage calculation will undoubtedly serve you well in your academic pursuits and future endeavors.
Latest Posts
Latest Posts
-
Which Tools Would You Use
Sep 14, 2025
-
Carboxylic Acid To An Aldehyde
Sep 14, 2025
-
The Teeny Tiny Woman Book
Sep 14, 2025
-
Words That Describe A Tree
Sep 14, 2025
-
Different Types Of Scatter Graphs
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 22 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.