What Is 25 Of 96
salachar
Sep 15, 2025 · 5 min read
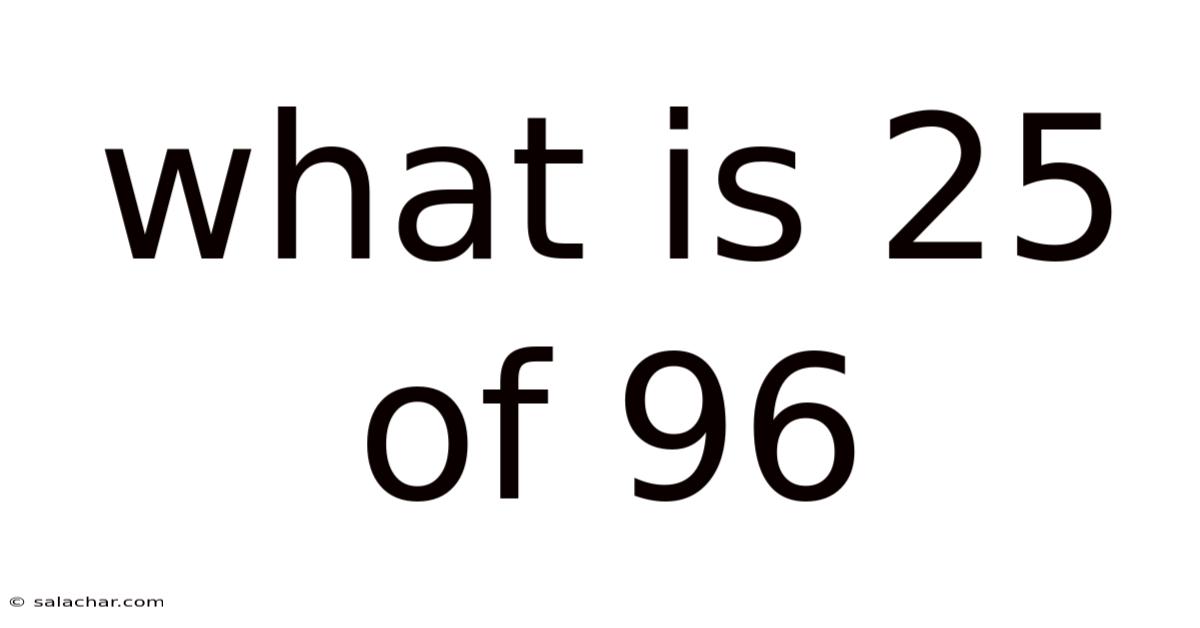
Table of Contents
What is 25/96? Understanding Fractions, Decimals, and Percentages
Finding the value of 25/96 might seem like a simple arithmetic problem, but it offers a great opportunity to explore fundamental mathematical concepts like fractions, decimals, and percentages. This article will delve into various methods of solving this fraction, providing a comprehensive understanding of the process and its implications. We'll also explore the broader context of working with fractions and their practical applications.
Understanding the Fraction 25/96
The fraction 25/96 represents a part of a whole. The number 25 is the numerator, indicating the number of parts we have, and 96 is the denominator, indicating the total number of equal parts that make up the whole. Understanding this basic structure is crucial for any further calculations.
Methods to Solve 25/96
There are several ways to determine the value of 25/96:
1. Simplification:
The first step in working with fractions is often to simplify them. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. In this case, the GCD of 25 and 96 is 1. Since the GCD is 1, the fraction is already in its simplest form and cannot be further simplified.
2. Conversion to Decimal:
Converting a fraction to a decimal involves dividing the numerator by the denominator. Using a calculator or performing long division:
25 ÷ 96 ≈ 0.2604
Therefore, 25/96 is approximately equal to 0.2604.
3. Conversion to Percentage:
To convert a fraction to a percentage, we first convert it to a decimal (as shown above) and then multiply by 100%.
0.2604 × 100% ≈ 26.04%
Thus, 25/96 represents approximately 26.04% of the whole.
Expanding on the Concepts
Let's explore the underlying mathematical concepts in more detail:
Fractions: A Foundation of Mathematics
Fractions are a fundamental concept in mathematics representing parts of a whole. They are expressed as a ratio of two integers, the numerator and the denominator. Fractions are used extensively in various fields, including:
- Cooking and Baking: Recipes often use fractions to specify ingredient quantities (e.g., 1/2 cup of flour).
- Engineering and Construction: Precise measurements and calculations often involve fractions.
- Finance: Fractions are crucial for understanding financial ratios and percentages.
- Data Analysis: Fractions and proportions are vital for interpreting data and drawing conclusions.
Decimals: An Alternative Representation
Decimals are another way to represent fractions. They use a base-10 system, making them convenient for calculations and comparisons. The decimal representation of 25/96 (approximately 0.2604) provides a more easily understood value for many applications. Decimals are commonly used in:
- Currency: Money is usually represented using decimals (e.g., $12.50).
- Scientific Measurements: Scientific data often involves decimal numbers for precision.
- Computer Programming: Decimals are fundamental for representing numerical data in computer systems.
Percentages: Expressing Proportions
Percentages express a fraction or decimal as a proportion of 100. They are a widely used way to represent parts of a whole and are particularly useful for comparisons and understanding proportions. Percentages are commonly used in:
- Statistics: Percentages are used to represent data and probabilities.
- Business and Finance: Percentages are vital for understanding profit margins, interest rates, and growth rates.
- Everyday Life: We encounter percentages in sales discounts, tax rates, and many other contexts.
Long Division: A Manual Approach
While calculators provide a quick solution, understanding long division is crucial for developing a deeper understanding of fractions and decimals. Let's manually divide 25 by 96:
0.2604...
96 | 25.0000
-0
250
-192
580
-576
40
-0
400
-384
16
As we can see, the division continues indefinitely, producing a repeating decimal. We usually round the result to a certain number of decimal places depending on the required accuracy.
Practical Applications and Real-World Examples
Understanding fractions, decimals, and percentages is vital for everyday life and professional applications. Here are a few examples:
- Calculating Discounts: If a store offers a 25% discount on an item priced at $96, the discount amount is (25/96) * $96 = $25.
- Sharing Resources: If 25 out of 96 people in a group are assigned a specific task, the fraction 25/96 represents the proportion of the group involved.
- Analyzing Data: In statistical analysis, ratios and proportions expressed as fractions or percentages are fundamental for understanding datasets and trends.
Frequently Asked Questions (FAQ)
-
Can 25/96 be simplified further? No, 25 and 96 share no common factors other than 1, meaning the fraction is already in its simplest form.
-
What is the exact decimal value of 25/96? The decimal value is a non-terminating, repeating decimal. We can only give an approximation, such as 0.2604.
-
How do I convert a percentage back to a fraction? Divide the percentage by 100 and simplify the resulting fraction. For example, 26.04% is equivalent to 26.04/100, which simplifies to 651/2500.
-
Why is it important to understand fractions, decimals, and percentages? These concepts are fundamental for numerous mathematical applications, making them crucial for various fields and everyday problem-solving.
Conclusion
Understanding the value of 25/96 involves more than just a simple calculation; it opens the door to a broader understanding of fractions, decimals, and percentages. These are fundamental mathematical concepts with far-reaching applications in various fields. By mastering these concepts, you gain a powerful toolset for solving problems and interpreting data in numerous real-world scenarios. The ability to convert between fractions, decimals, and percentages ensures flexibility and efficiency in tackling a wide range of mathematical problems. This understanding is not just about finding the answer to a single fraction; it's about building a strong foundation for more complex mathematical explorations.
Latest Posts
Latest Posts
-
What Are Multiples Of 21
Sep 16, 2025
-
What Is An Opposite Integer
Sep 16, 2025
-
3 Little Pigs Wolf Perspective
Sep 16, 2025
-
What Times What Is 26
Sep 16, 2025
-
People Born On 8 August
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 96 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.