What Is 30 Of 36
salachar
Sep 08, 2025 · 6 min read
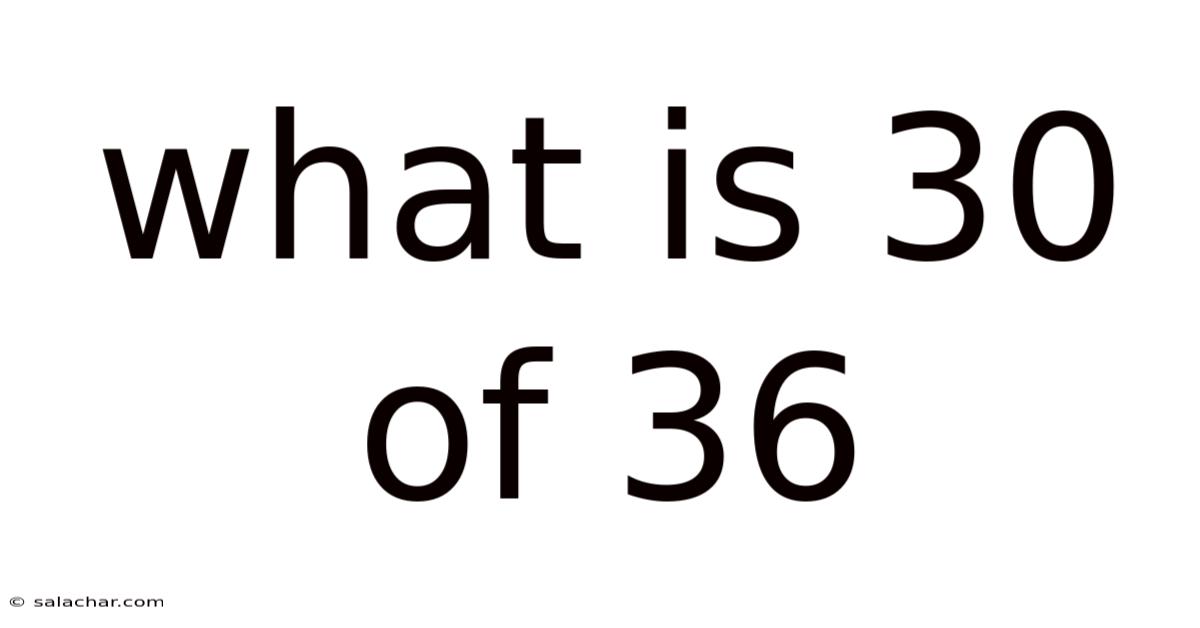
Table of Contents
What is 30 of 36? Understanding Fractions, Percentages, and Ratios
"What is 30 of 36?" This seemingly simple question opens the door to a deeper understanding of fundamental mathematical concepts: fractions, percentages, and ratios. While the immediate answer might seem straightforward, exploring the different ways to interpret and solve this problem reveals valuable insights into mathematical relationships and problem-solving strategies. This article will delve into the various approaches to answering this question, providing a comprehensive explanation suitable for learners of all levels.
Understanding the Core Concepts: Fractions, Percentages, and Ratios
Before we tackle "30 of 36," let's establish a firm grasp of the three core mathematical concepts involved:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In the context of "30 of 36," 30 represents the part, and 36 represents the whole. Thus, the fraction is 30/36.
-
Percentages: A percentage is a way of expressing a fraction as a proportion of 100. It indicates how many parts out of 100 represent a given quantity. To find the percentage, we convert the fraction to an equivalent fraction with a denominator of 100 or we perform a calculation.
-
Ratios: A ratio expresses the relative size of two or more values. It shows the quantitative relationship between two or more quantities. "30 of 36" can be expressed as a ratio of 30:36, indicating the proportion of 30 to 36.
Calculating 30 of 36: Different Approaches
There are several ways to determine the value of 30 out of 36. Let's explore the most common methods:
1. Simplifying the Fraction:
The simplest approach is to express "30 of 36" as a fraction (30/36) and then simplify it to its lowest terms. We find the greatest common divisor (GCD) of 30 and 36, which is 6. Dividing both the numerator and the denominator by 6, we get:
30 ÷ 6 = 5 36 ÷ 6 = 6
Therefore, 30/36 simplifies to 5/6. This means 30 is 5/6 of 36.
2. Converting to a Percentage:
To express "30 of 36" as a percentage, we can use the simplified fraction (5/6) or the original fraction (30/36). Here's how:
-
Using the simplified fraction: Divide the numerator (5) by the denominator (6): 5 ÷ 6 ≈ 0.8333. Multiply this decimal by 100 to express it as a percentage: 0.8333 x 100 ≈ 83.33%. Therefore, 30 is approximately 83.33% of 36.
-
Using the original fraction: Divide the numerator (30) by the denominator (36): 30 ÷ 36 ≈ 0.8333. Multiply this decimal by 100 to get the percentage: 0.8333 x 100 ≈ 83.33%.
3. Using Decimal Representation:
We can convert the fraction 30/36 into a decimal by performing the division: 30 ÷ 36 ≈ 0.8333. This decimal represents the proportion of 30 out of 36.
4. Understanding the Ratio:
The ratio of 30 to 36 is 30:36. Like the fraction, this ratio can be simplified by dividing both numbers by their GCD (6):
30 ÷ 6 = 5 36 ÷ 6 = 6
The simplified ratio is 5:6. This represents the same proportional relationship as the simplified fraction 5/6.
Practical Applications and Real-World Examples
Understanding "30 of 36" and its different representations extends beyond simple mathematical exercises. Here are some real-world scenarios where these concepts come into play:
-
Test Scores: If a student answers 30 questions correctly out of a total of 36, their score is 30/36 or 83.33%.
-
Sales Targets: A salesperson aiming to sell 36 units achieves 30 sales. Their performance is 30/36 or 83.33% of the target.
-
Project Completion: If a project involves 36 tasks and 30 are completed, the project's progress is 30/36 or 83.33% complete.
-
Surveys and Data Analysis: In a survey of 36 people, 30 respond positively. The positive response rate is 30/36 or 83.33%.
-
Recipe Scaling: If a recipe calls for 36 units of an ingredient, and you only have 30, you can adjust the other ingredients proportionally based on the fraction 30/36 or 5/6.
Expanding the Understanding: Further Exploration
While we've focused on the calculation of "30 of 36," let's expand our understanding to encompass related concepts:
-
Proportionality: The relationship between 30 and 36 is proportional. This means that if we scale 36 up or down, the corresponding value of 30 will also scale proportionally.
-
Inverse Proportionality: Consider the scenario where 30 represents the time taken to complete a task and 36 represents the number of workers. In this case, an inverse proportional relationship exists. As the number of workers increases, the time taken decreases.
-
Understanding Error Margins: In real-world scenarios, it's crucial to consider potential errors. For example, if 30 represents a measurement, an understanding of the error margin associated with that measurement is crucial for accurate interpretation.
-
Applications in Geometry: Concepts of fractions, percentages, and ratios are fundamental in geometry, particularly when dealing with areas, volumes, and proportions of shapes.
Frequently Asked Questions (FAQ)
Q1: Can 30/36 be simplified further than 5/6?
A1: No, 5/6 is the simplified form because 5 and 6 have no common divisors other than 1.
Q2: How do I convert a fraction to a percentage?
A2: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100.
Q3: What is the difference between a fraction and a ratio?
A3: While both represent a relationship between two or more quantities, a fraction represents a part of a whole, while a ratio can compare any two quantities, not necessarily parts of a whole. However, fractions can be expressed as ratios and vice versa.
Q4: Are there other ways to represent 30 of 36 besides fractions, percentages, and ratios?
A4: Yes, you could represent it graphically using a pie chart or a bar graph, visually showing the proportion of 30 out of 36.
Q5: How can I apply these concepts to more complex problems?
A5: The principles of fractions, percentages, and ratios are essential building blocks for tackling more advanced mathematical concepts in algebra, calculus, and statistics.
Conclusion: Beyond the Numbers
"What is 30 of 36?" The answer, simply stated, is 5/6, 83.33%, or a 5:6 ratio. But the true value lies in the journey of understanding the fundamental mathematical principles involved. By exploring fractions, percentages, ratios, and their various applications, we not only solve this specific problem but also equip ourselves with the tools to tackle a broader range of mathematical challenges in various fields of study and everyday life. The ability to understand and apply these concepts is a crucial skill for success in numerous academic and professional pursuits. So, the next time you encounter a similar problem, remember the power of breaking down complex questions into smaller, more manageable parts and leveraging the fundamental principles of mathematics to find a solution.
Latest Posts
Latest Posts
-
Plaster Of Paris Chemical Formula
Sep 09, 2025
-
Is Mgo An Ionic Compound
Sep 09, 2025
-
How Much Is 2 Hours
Sep 09, 2025
-
Words That Start With Biblio
Sep 09, 2025
-
Biotic Factors In A Rainforest
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.