What Is 40 Of 32
salachar
Sep 07, 2025 · 5 min read
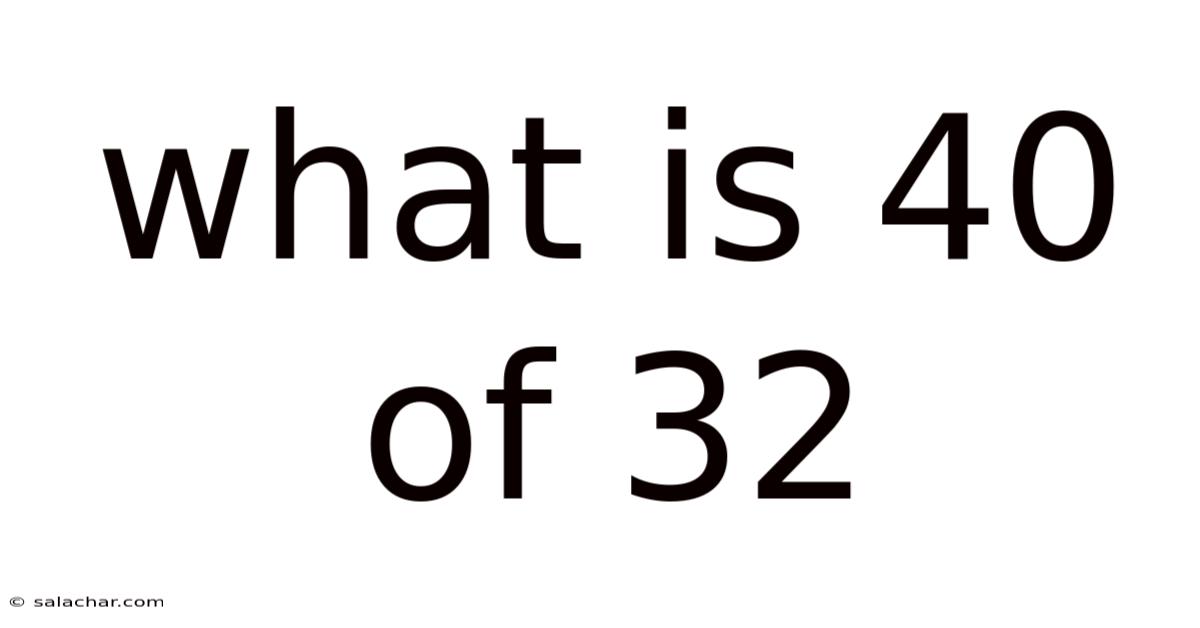
Table of Contents
What is 40% of 32? A Deep Dive into Percentages and Their Applications
Finding 40% of 32 might seem like a simple arithmetic problem, but it opens a door to a broader understanding of percentages, their practical applications, and the underlying mathematical principles. This article will not only solve this specific problem but also delve into the different methods of calculation, explore real-world examples, and address frequently asked questions about percentages. Understanding percentages is crucial in various fields, from finance and budgeting to data analysis and scientific research. This guide aims to equip you with the knowledge and skills to confidently tackle percentage calculations in any context.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 40% can be understood as 40 parts out of 100 equal parts of a whole. This representation allows for easy comparison and interpretation of proportions across different datasets. We often use the "%" symbol to represent percentages.
Method 1: Converting Percentage to Decimal
The most straightforward method to calculate 40% of 32 involves converting the percentage into a decimal. To do this, we divide the percentage by 100:
40% = 40 / 100 = 0.4
Now, we multiply this decimal by the number we want to find the percentage of:
0.4 * 32 = 12.8
Therefore, 40% of 32 is 12.8.
Method 2: Using Fractions
Another approach is to express the percentage as a fraction. 40% can be written as 40/100, which simplifies to 2/5. We then multiply this fraction by 32:
(2/5) * 32 = 64/5 = 12.8
This method confirms our previous result: 40% of 32 is 12.8.
Method 3: Proportion Method
The proportion method provides a more visual and intuitive understanding of percentage calculations. We set up a proportion:
40/100 = x/32
Here, 'x' represents the unknown value (40% of 32). To solve for 'x', we cross-multiply:
40 * 32 = 100 * x
1280 = 100x
x = 1280 / 100 = 12.8
Again, we arrive at the same answer: 40% of 32 is 12.8.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in numerous real-life scenarios:
-
Finance: Calculating interest on loans, savings accounts, and investments heavily relies on percentage calculations. For example, determining the interest earned on a savings account with an annual interest rate of 4% requires calculating the percentage of the principal amount.
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. If a $50 item is discounted by 20%, calculating the discount amount and the final price involves percentage calculations.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the taxable amount. Understanding these percentages is crucial for accurate financial planning and budgeting.
-
Data Analysis: In statistics and data analysis, percentages are used extensively to represent proportions, trends, and changes in data. For instance, analyzing survey results often involves calculating the percentage of respondents who chose a particular option.
-
Scientific Research: Percentages are used to represent experimental results, error margins, and other critical data points in scientific studies. Accurate percentage calculations are essential for drawing valid conclusions from research data.
Beyond the Basics: More Complex Percentage Problems
While finding 40% of 32 is a relatively simple calculation, the underlying principles can be applied to more complex problems. For example:
-
Finding the original value: If you know that 40% of a number is 12.8, you can work backward to find the original number. This involves setting up an equation: 0.4x = 12.8, where 'x' is the original number. Solving for 'x' gives you x = 32.
-
Calculating percentage increase or decrease: Determining the percentage change between two values requires calculating the difference between the values, dividing by the original value, and multiplying by 100. For example, if a value increases from 20 to 25, the percentage increase is ((25-20)/20) * 100 = 25%.
-
Compound percentages: In situations involving multiple percentage changes, the order of operations can affect the final result. For instance, a 10% increase followed by a 10% decrease does not result in the original value.
-
Percentage points: It is important to distinguish between percentage change and percentage points. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase in the value itself.
Frequently Asked Questions (FAQ)
Q: How can I calculate percentages quickly without a calculator?
A: For simpler percentages like 10%, 25%, or 50%, mental math techniques are useful. 10% is simply dividing by 10. 50% is dividing by 2. 25% is dividing by 4. For other percentages, approximating or using fractions can simplify calculations.
Q: What are some common mistakes people make when working with percentages?
A: Common errors include incorrect decimal conversions, confusion between percentage change and percentage points, and improper order of operations in complex problems. Carefully reviewing the problem statement and using multiple methods to verify results can help minimize these errors.
Q: Are there online tools or software that can help with percentage calculations?
A: Yes, many online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) offer built-in functions for calculating percentages. These tools can be particularly helpful for complex calculations or large datasets.
Conclusion: Mastering Percentages for Everyday Life
Understanding percentages is a fundamental skill with broad applications in various aspects of life. This article has demonstrated different methods to calculate percentages, specifically focusing on finding 40% of 32, and highlighted the importance of mastering this skill for practical applications in finance, sales, data analysis, and other fields. By grasping the underlying mathematical principles and practicing different approaches, you can confidently tackle percentage problems of varying complexity and apply this knowledge to make informed decisions in your personal and professional life. Remember to always double-check your calculations and consider using alternative methods to verify your results. The ability to confidently and accurately calculate percentages is an invaluable asset in navigating the numerical world around us.
Latest Posts
Latest Posts
-
What Times What Equals 37
Sep 08, 2025
-
Is Tap Water A Mixture
Sep 08, 2025
-
Pluralizing Names Ending In S
Sep 08, 2025
-
Chemistry In Our Daily Lives
Sep 08, 2025
-
Uses Of Monitor In Computer
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.