What Is 50 Of 120
salachar
Sep 13, 2025 · 5 min read
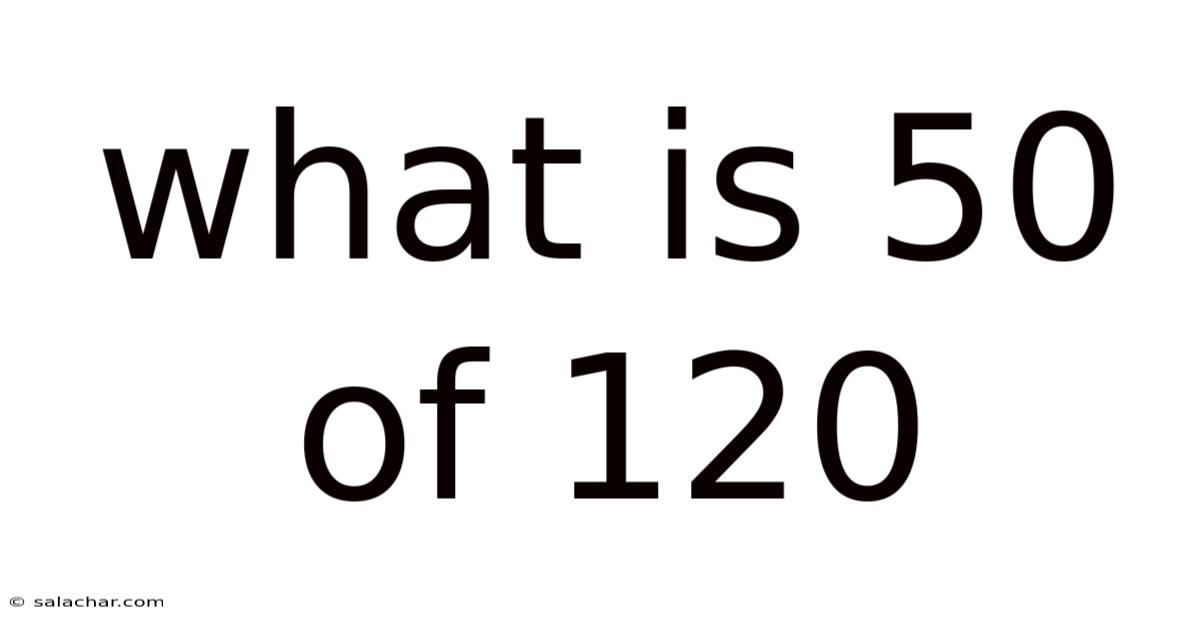
Table of Contents
What is 50 of 120? Understanding Fractions, Percentages, and Ratios
Finding "50 of 120" involves understanding fundamental mathematical concepts like fractions, percentages, and ratios. This seemingly simple question opens the door to a deeper exploration of these interconnected ideas, which are crucial in various aspects of life, from everyday calculations to complex scientific analyses. This article will not only answer the question directly but also provide a comprehensive guide to understanding the underlying principles, equipping you with the skills to tackle similar problems confidently.
Understanding the Question
The phrase "50 of 120" implies a part-to-whole relationship. We're looking for a specific portion (50) of a larger quantity (120). This can be expressed in several ways: as a fraction, a percentage, or a ratio. Let's explore each representation.
1. Expressing "50 of 120" as a Fraction
A fraction represents a part of a whole. In this case, the part is 50, and the whole is 120. Therefore, "50 of 120" can be written as the fraction 50/120.
-
Simplification: This fraction can be simplified by finding the greatest common divisor (GCD) of 50 and 120. The GCD of 50 and 120 is 10. Dividing both the numerator (50) and the denominator (120) by 10, we get the simplified fraction 5/12. This means that 50 is 5/12 of 120.
-
Decimal Representation: To express the fraction as a decimal, we divide the numerator by the denominator: 5 ÷ 12 ≈ 0.4167. This means that 50 is approximately 0.4167 of 120.
2. Expressing "50 of 120" as a Percentage
A percentage represents a fraction out of 100. To express 50/120 as a percentage, we first convert the fraction to a decimal (as shown above: approximately 0.4167). Then, we multiply the decimal by 100:
0.4167 x 100 ≈ 41.67%
Therefore, 50 is approximately 41.67% of 120.
3. Expressing "50 of 120" as a Ratio
A ratio compares two quantities. In this case, the ratio of 50 to 120 can be written as 50:120. Like the fraction, this ratio can be simplified by dividing both numbers by their GCD (10), resulting in the simplified ratio 5:12. This signifies that for every 5 units of the part, there are 12 units in the whole.
Practical Applications and Real-World Examples
Understanding how to calculate "50 of 120" and similar problems has numerous real-world applications:
-
Sales and Discounts: Imagine a store offering a 50% discount on an item originally priced at $120. Calculating 50% of 120 helps determine the discount amount ($60) and the final price ($60).
-
Surveys and Statistics: If 50 out of 120 respondents answered "yes" to a survey question, calculating the percentage (approximately 41.67%) provides a valuable insight into public opinion.
-
Recipe Scaling: If a recipe calls for 50 grams of flour for 120 cookies, adjusting the recipe to make a smaller batch involves proportional reasoning, similar to calculating "50 of 120."
-
Financial Calculations: Determining the interest earned on an investment, calculating the portion of a budget allocated to a specific expense, or understanding profit margins all require calculating a part of a whole, just like this example.
-
Engineering and Construction: Proportionate scaling of blueprints or calculating material quantities involves the same principles. For instance, if a plan calls for 120 units of material X and you need only 50 units, the calculation is crucial for accurate estimation.
-
Data Analysis: Many data analysis tasks involve calculating proportions or percentages of datasets, directly applying these foundational mathematical skills.
Further Exploration: Proportions and Cross-Multiplication
The relationship between 50 and 120 can also be understood using proportions. A proportion is an equation stating that two ratios are equal. We can set up a proportion to find an unknown value:
50/120 = x/100 (where 'x' represents the percentage)
To solve for 'x', we can use cross-multiplication:
120x = 5000
x = 5000/120 ≈ 41.67
This confirms our earlier calculation that 50 is approximately 41.67% of 120. Cross-multiplication is a powerful tool for solving various proportion problems.
Expanding Understanding: Beyond Simple Calculations
While this article focuses on calculating "50 of 120," the underlying concepts extend to more complex scenarios. Consider the following:
-
Compound Proportions: Problems involving multiple proportional relationships. For example, calculating the total cost of materials considering both quantity and price fluctuations.
-
Inverse Proportions: Situations where one quantity increases while another decreases (e.g., the time taken to complete a task decreases as the number of workers increases).
-
Advanced Statistical Analysis: Understanding proportions and percentages is fundamental to various statistical techniques used in analyzing data and drawing meaningful conclusions.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of the fraction 50/120?
- A: The simplest form is 5/12.
-
Q: How do I convert a fraction to a percentage?
- A: Divide the numerator by the denominator, then multiply the result by 100.
-
Q: What if I need to find a different part of 120, say 75 of 120?
- A: The same principles apply. You would calculate 75/120, simplify the fraction, and then convert to a percentage if needed.
-
Q: Are there any online calculators that can help with these calculations?
- A: Yes, many online calculators can perform fraction simplification, percentage calculations, and ratio comparisons. These tools can be useful for verifying your calculations.
-
Q: How do I apply these concepts to real-world problems?
- A: The key is to identify the part and the whole in a given situation. Once you've identified these, you can express the relationship as a fraction, percentage, or ratio and perform the necessary calculations.
Conclusion
Calculating "50 of 120" is more than just a simple mathematical operation. It's a gateway to understanding fundamental mathematical concepts with broad applicability. Mastering the skills of fraction simplification, percentage conversion, and ratio analysis empowers you to tackle diverse problems across various disciplines, enhancing your analytical skills and problem-solving abilities in both academic and professional settings. This knowledge serves as a solid foundation for more advanced mathematical explorations and real-world problem-solving. Remember to always break down the problem into its core components, clearly identifying the "part" and the "whole" before applying the appropriate method.
Latest Posts
Latest Posts
-
Color Of Flame Calcium Chloride
Sep 13, 2025
-
Derivative Of Sinh And Cosh
Sep 13, 2025
-
First 10 Multiples Of 6
Sep 13, 2025
-
How To Draw A Bum
Sep 13, 2025
-
Methanol And Salicylic Acid Odor
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.