What Is 6 Of 15
salachar
Sep 15, 2025 · 6 min read
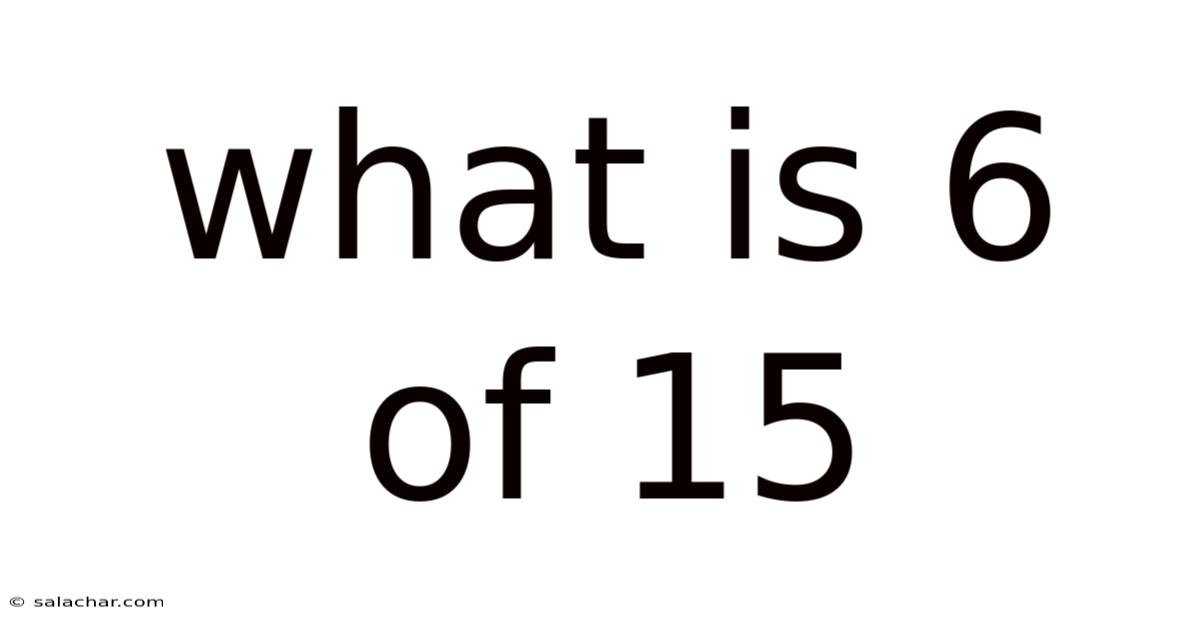
Table of Contents
What is 6 out of 15? Understanding Fractions, Percentages, and Ratios
Understanding fractions, percentages, and ratios is a fundamental skill in mathematics with applications across various fields, from everyday budgeting to complex scientific calculations. This article explores the meaning of "6 out of 15," explaining how to represent it as a fraction, decimal, percentage, and ratio, and providing practical examples to solidify your understanding. We'll also delve into the broader concept of proportional reasoning.
Introduction: Deconstructing "6 out of 15"
The phrase "6 out of 15" describes a part-to-whole relationship. It signifies that 6 is a portion of a larger whole consisting of 15 units. This simple statement forms the basis for understanding various mathematical concepts. We can represent this relationship in several ways, each offering unique insights and applications. This article aims to clarify these representations and their interconnectedness.
1. Representing "6 out of 15" as a Fraction
The most direct way to represent "6 out of 15" is as a fraction: 6/15. The numerator (6) represents the part, and the denominator (15) represents the whole. This fraction is not in its simplest form, however. To simplify, we find the greatest common divisor (GCD) of both the numerator and the denominator. The GCD of 6 and 15 is 3. Dividing both the numerator and the denominator by 3, we get:
6 ÷ 3 = 2 15 ÷ 3 = 5
Therefore, the simplified fraction is 2/5. This means that 6 out of 15 is equivalent to 2 out of 5. Both fractions represent the same proportion.
2. Converting the Fraction to a Decimal
To convert the fraction 2/5 to a decimal, we perform the division: 2 ÷ 5 = 0.4. Therefore, "6 out of 15" is equal to 0.4 as a decimal. This decimal representation is useful in calculations involving other decimals or when using calculators or computer programs.
3. Expressing "6 out of 15" as a Percentage
A percentage expresses a fraction or decimal as a proportion of 100. To convert the decimal 0.4 to a percentage, we multiply by 100: 0.4 × 100 = 40%. Therefore, "6 out of 15" is equal to 40%. This representation is commonly used to express proportions in everyday life, such as discounts, grades, or statistical data.
4. Understanding "6 out of 15" as a Ratio
A ratio compares two or more quantities. "6 out of 15" can be expressed as the ratio 6:15 or, in its simplified form after dividing both sides by the GCD (3), as the ratio 2:5. This ratio indicates that for every 2 units of one quantity, there are 5 units of the total quantity. Ratios are useful in comparing different quantities or proportions.
5. Practical Applications and Real-World Examples
Let's illustrate the practical applications of understanding "6 out of 15" with some real-world scenarios:
-
Test Scores: Imagine a student answered 6 questions correctly out of a total of 15 questions on a test. Their score would be 6/15, which simplifies to 2/5 or 40%. This clearly shows their performance compared to the total number of questions.
-
Inventory Management: A shop has 15 shirts, 6 of which are blue. The ratio of blue shirts to the total number of shirts is 6:15 or 2:5. This helps in managing stock and ordering more blue shirts if necessary.
-
Survey Results: In a survey of 15 people, 6 preferred a particular brand of coffee. The percentage of people who preferred this brand is 40%. This information is crucial for market research and business decisions.
-
Recipe Scaling: A recipe calls for 6 tablespoons of sugar in a mixture of 15 tablespoons of ingredients. This can be simplified to 2 tablespoons of sugar for every 5 tablespoons of the total mixture. This allows you to easily scale the recipe up or down.
-
Probability: If you have 15 equally likely outcomes and 6 of them are favorable, the probability of a favorable outcome is 6/15 or 2/5 (or 40%).
6. Expanding the Concept: Proportional Reasoning
The concept of "6 out of 15" is closely linked to proportional reasoning. Proportional reasoning involves understanding the relationships between quantities and how changes in one quantity affect other related quantities. For example, if we double the number of questions on the test (from 15 to 30) and the student maintains the same proportion of correct answers, they would correctly answer 12 questions (6 x 2 = 12). This demonstrates the principle of proportionality. Mastering proportional reasoning is crucial for problem-solving in various mathematical contexts.
7. Advanced Concepts and Further Exploration
While "6 out of 15" is a seemingly simple concept, it opens the door to more advanced mathematical concepts:
-
Percentage Increase/Decrease: Understanding percentages allows you to calculate percentage increases or decreases. For instance, if the number of blue shirts increases from 6 to 9 out of 15, the increase is 3 shirts, representing a 50% increase.
-
Ratio and Proportion Problems: Numerous word problems involve ratios and proportions. Solving these problems requires understanding how to set up and solve equations involving ratios and fractions.
-
Statistical Analysis: Percentages and ratios are fundamental to statistical analysis, allowing for the comparison of different groups and the identification of trends.
8. Frequently Asked Questions (FAQ)
-
Q: Is 6/15 the same as 2/5?
- A: Yes, 6/15 and 2/5 are equivalent fractions. They represent the same proportion.
-
Q: How do I convert a fraction to a percentage?
- A: Divide the numerator by the denominator, then multiply the result by 100 and add the % symbol.
-
Q: What is the difference between a fraction and a ratio?
- A: Both fractions and ratios represent a part-to-whole relationship. However, fractions represent a part of a whole, while ratios can compare any two or more quantities.
-
Q: Can I use a calculator to simplify fractions?
- A: Many calculators have a function to simplify fractions. Alternatively, you can manually find the GCD of the numerator and denominator.
9. Conclusion: Mastering the Fundamentals
Understanding "6 out of 15" as a fraction, decimal, percentage, and ratio is a crucial step in mastering fundamental mathematical concepts. This seemingly simple concept underpins more complex mathematical operations and problem-solving skills, finding applications in various fields. By mastering these basic principles, you build a solid foundation for tackling more advanced mathematical challenges and effectively applying these concepts in real-world situations. The ability to translate between these different representations allows for flexibility in calculations and a deeper understanding of proportional relationships. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Does Normal Force Do Work
Sep 15, 2025
-
Three Billy Goats Gruff Summary
Sep 15, 2025
-
Prime Numbers And Odd Numbers
Sep 15, 2025
-
Electron Flow Vs Conventional Current
Sep 15, 2025
-
Things Shaped Like A Cone
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.