What Is 60 Of 160
salachar
Sep 11, 2025 · 5 min read
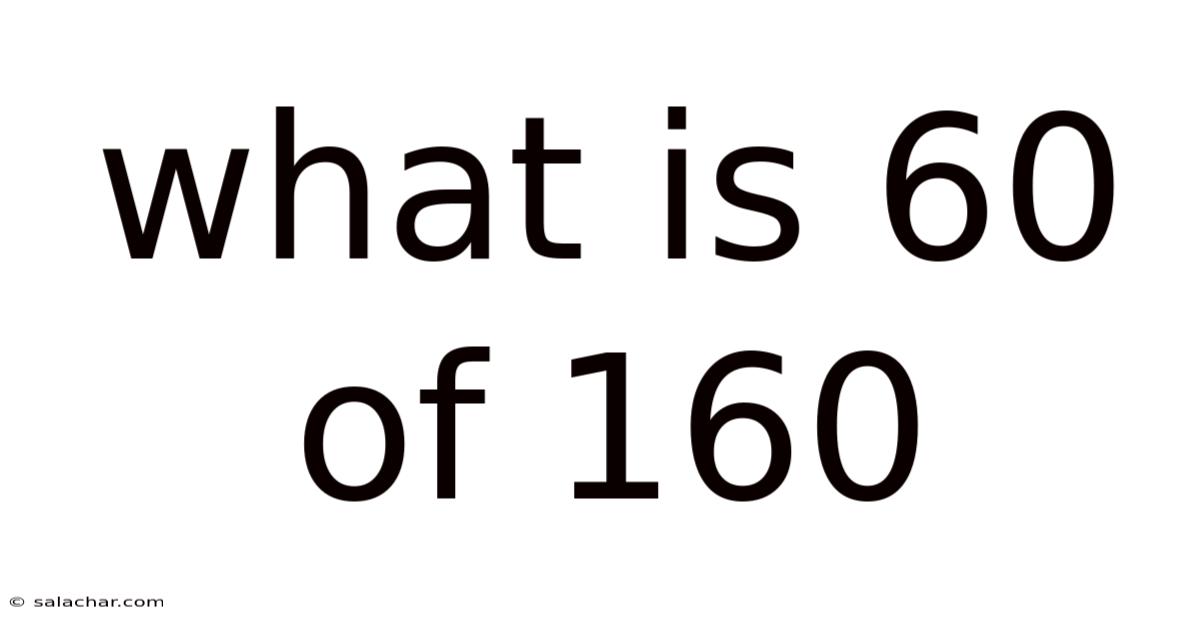
Table of Contents
What is 60 of 160? Understanding Percentages and Proportions
This article will delve into the seemingly simple question: "What is 60 of 160?" While the answer might seem immediately obvious to some, understanding the underlying mathematical concepts—percentages and proportions—is crucial for a wide range of applications, from everyday budgeting to complex scientific calculations. We'll explore various methods to solve this problem, explain the reasoning behind each approach, and even touch upon the broader implications of proportional reasoning.
Introduction: The Fundamentals of Percentages and Proportions
The question "What is 60 of 160?" essentially asks us to find what percentage 60 represents of the whole, 160. Percentages are a way of expressing a fraction as a part of 100. Proportions, on the other hand, deal with the relationship between two ratios. They are essentially equivalent fractions. Mastering both concepts is key to solving this and similar problems.
Method 1: Calculating the Percentage Directly
The most straightforward way to solve this is to directly calculate the percentage. We can do this using the following formula:
(Part / Whole) * 100%
In this case, the part is 60, and the whole is 160. Substituting these values into the formula, we get:
(60 / 160) * 100%
This simplifies to:
0.375 * 100% = 37.5%
Therefore, 60 is 37.5% of 160.
Method 2: Using Proportions
We can also solve this problem using proportions. We can set up a proportion as follows:
60 / 160 = x / 100
Here, 'x' represents the percentage we are trying to find. To solve for 'x', we can cross-multiply:
60 * 100 = 160 * x
6000 = 160x
Now, we divide both sides by 160:
x = 6000 / 160 = 37.5
Therefore, once again, we find that 60 is 37.5% of 160. This method reinforces the connection between percentages and the concept of equivalent fractions.
Method 3: Simplifying the Fraction
Before calculating the percentage, we can simplify the fraction 60/160. Both the numerator and the denominator are divisible by 20:
60 / 20 = 3
160 / 20 = 8
This simplifies the fraction to 3/8. Now, we can convert this simplified fraction to a percentage:
(3 / 8) * 100%
0.375 * 100% = 37.5%
This method demonstrates the importance of simplifying fractions to make calculations easier and less prone to error. It highlights the equivalence between different representations of the same ratio.
Understanding the Result: What Does 37.5% Mean?
The result, 37.5%, tells us that 60 represents almost 38 out of every 100 parts of 160. This percentage can be used to make comparisons and draw conclusions. For example, if 160 represents the total number of students in a class, and 60 students passed an exam, then the pass rate is 37.5%.
Real-World Applications of Percentage and Proportional Reasoning
The ability to calculate percentages and proportions is fundamental to numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, profit margins, and tax amounts.
- Science: Determining concentrations of solutions, analyzing experimental data, and understanding ratios in chemical reactions.
- Everyday Life: Estimating tips, calculating sales tax, comparing prices, and understanding statistics in news reports.
- Business: Analyzing sales figures, market share, and cost-benefit ratios.
- Engineering: Scaling designs, calculating material requirements, and understanding load distribution.
Expanding the Understanding: Beyond the Basics
While we've focused on finding 60 as a percentage of 160, the underlying principles can be applied to a much broader range of problems. For instance:
- Finding the Whole: If 37.5% of a number is 60, what is the number? This requires working backward from the percentage to find the original whole.
- Finding the Part: What is 25% of 160? This involves applying the percentage formula to a different scenario.
- Comparing Proportions: Which is larger: 60 out of 160 or 80 out of 200? This involves comparing the ratios to determine which represents a greater proportion.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Yes, absolutely. Calculators simplify the calculations, especially when dealing with more complex percentages or fractions.
-
Q: What if the numbers were decimals or fractions? A: The same principles apply. You would simply substitute the decimal or fractional values into the percentage formula or set up a proportion and solve accordingly.
-
Q: Are there other ways to solve this problem? A: Yes, there are more advanced methods involving algebraic equations and other mathematical techniques. However, the methods outlined above are sufficient for most everyday applications.
-
Q: Why is understanding percentages and proportions important? A: Because these concepts are foundational to many areas of mathematics and are essential for critical thinking and problem-solving skills in numerous fields.
Conclusion: Mastering the Fundamentals for Future Success
The seemingly simple question of "What is 60 of 160?" opens the door to a deeper understanding of percentages and proportions. These mathematical concepts are not just abstract ideas; they are powerful tools for navigating the complexities of the world around us. By mastering these fundamentals, we equip ourselves with essential skills for success in various academic, professional, and personal endeavors. The ability to accurately calculate percentages and proportions is a valuable skill that translates across numerous disciplines and empowers us to make informed decisions in a variety of contexts. The methods explored in this article offer a solid foundation for tackling more complex problems involving proportional reasoning and percentage calculations in the future. Remember the core concepts – the relationship between parts and wholes, the equivalence of fractions, and the power of simplifying calculations. With practice, these concepts will become second nature, enabling you to confidently solve a wide array of problems involving ratios and percentages.
Latest Posts
Latest Posts
-
What Are Variables In Coding
Sep 11, 2025
-
Freezing Point Of Water Kelvin
Sep 11, 2025
-
What Does A Camel Say
Sep 11, 2025
-
Examples Of Density Dependent Factors
Sep 11, 2025
-
Highest 2 Digit Prime Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.