What Is 65 Of 200
salachar
Sep 12, 2025 · 5 min read
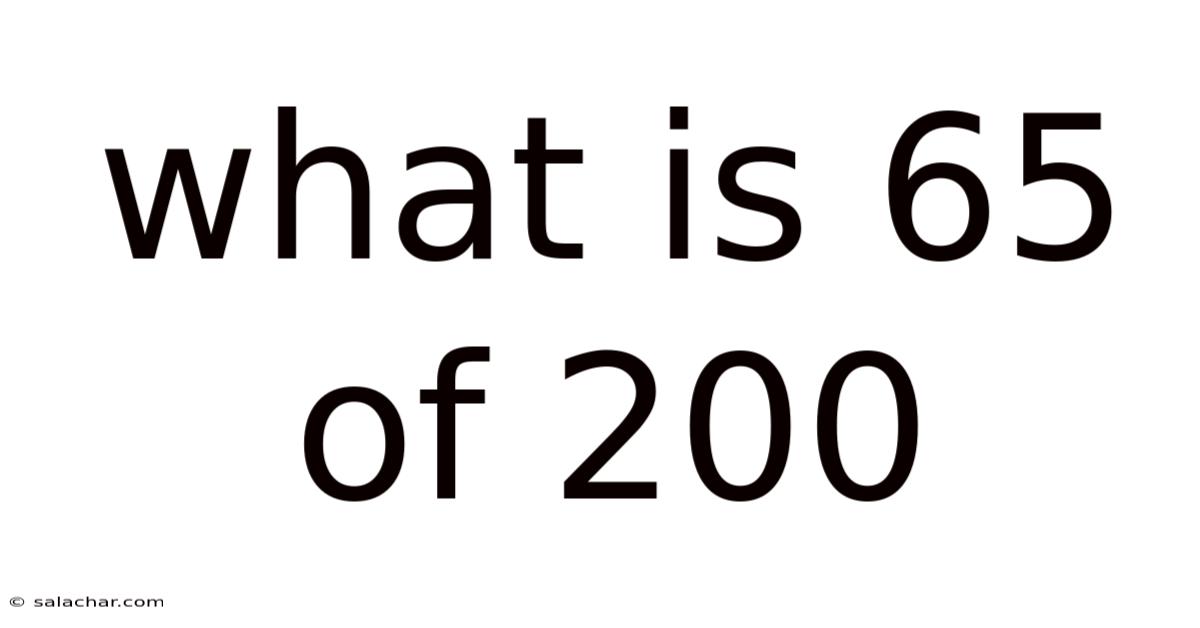
Table of Contents
What is 65% of 200? A Deep Dive into Percentages and Their Applications
Finding 65% of 200 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in various fields. This article will not only show you how to calculate 65% of 200 but will also explore the underlying principles of percentages, different methods of calculation, and real-world examples where this type of calculation is crucial. We'll delve into the theory behind percentages, explore various approaches to solving percentage problems, and finally, answer some frequently asked questions.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." The symbol "%" is used to represent percentage. Therefore, 65% can be written as 65/100 or 0.65. Understanding this basic concept is key to solving any percentage problem. In our case, finding 65% of 200 means finding 65 parts out of 100 parts of 200.
Methods for Calculating 65% of 200
There are several ways to calculate 65% of 200. Let's explore the most common methods:
1. The Decimal Method:
This is arguably the most straightforward method. We convert the percentage to a decimal and then multiply it by the number.
-
Step 1: Convert the percentage to a decimal: 65% is equivalent to 65/100 = 0.65
-
Step 2: Multiply the decimal by the number: 0.65 x 200 = 130
Therefore, 65% of 200 is 130.
2. The Fraction Method:
This method involves converting the percentage to a fraction and then performing the calculation.
-
Step 1: Convert the percentage to a fraction: 65% is equivalent to 65/100. This fraction can be simplified to 13/20.
-
Step 2: Multiply the fraction by the number: (13/20) x 200 = 13 x 10 = 130
Again, we find that 65% of 200 is 130.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value.
-
Step 1: Set up a proportion: We can set up a proportion as follows: 65/100 = x/200, where 'x' represents the unknown value (65% of 200).
-
Step 2: Cross-multiply: Cross-multiplying gives us: 100x = 65 x 200
-
Step 3: Solve for x: 100x = 13000. Dividing both sides by 100 gives x = 130
Once again, we arrive at the answer: 65% of 200 is 130.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is incredibly useful in a wide range of situations, both in everyday life and in professional settings. Here are just a few examples:
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages. Calculating the discount amount allows consumers to determine the final price. For example, a 65% discount on a $200 item would result in a saving of $130.
-
Taxes and Interest: Understanding percentages is crucial for calculating taxes, interest on loans, and investment returns. For instance, calculating the amount of sales tax on a purchase involves determining a percentage of the total cost.
-
Statistics and Data Analysis: Percentages are extensively used in statistics to represent proportions and changes in data. They are essential for interpreting data sets and drawing conclusions. For example, understanding the percentage change in sales figures from one year to the next helps businesses make informed decisions.
-
Financial Planning: Percentages are fundamental to financial planning, allowing individuals to track their savings, investments, and expenses. For example, budgeting often involves allocating a certain percentage of income to different categories.
-
Scientific Calculations: Many scientific calculations involve percentages, such as calculating the concentration of a solution or expressing the probability of an event.
-
Grading and Assessments: In education, grades are often expressed as percentages, reflecting the proportion of correct answers on a test or assignment. Understanding percentages is crucial for students to track their academic progress.
Further Exploring Percentage Concepts
While calculating 65% of 200 is relatively straightforward, understanding percentages more deeply involves grasping related concepts:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. For example, determining the percentage increase in sales from one year to the next.
-
Percentage Points: It’s important to distinguish between percentage points and percentage changes. A change from 20% to 25% is a 5 percentage point increase, but it represents a 25% increase relative to the initial value.
-
Compound Interest: Compound interest is a powerful concept that involves earning interest on both the principal amount and accumulated interest. Understanding how compound interest works relies heavily on percentage calculations.
-
Proportions and Ratios: Percentages are intrinsically linked to proportions and ratios. They are different ways to express the same fundamental relationship between two quantities.
Frequently Asked Questions (FAQ)
Q: How can I calculate percentages quickly in my head?
A: For simple percentages like 10%, 20%, 50%, etc., mental calculation is often possible. For example, 10% of a number is simply one-tenth of the number. For other percentages, rounding to simpler percentages can provide a good estimate.
Q: Are there any online calculators or tools to help with percentage calculations?
A: Yes, numerous online calculators and tools are available to help with percentage calculations. These can be particularly useful for more complex calculations or for checking your work.
Q: What if I need to find a percentage of a number that isn't a whole number?
A: The methods described above work equally well for non-whole numbers. Simply substitute the non-whole number into the calculations.
Q: How can I improve my understanding of percentages?
A: Practice is key! Try solving different percentage problems and using various methods to build your confidence and understanding. Also, consider exploring online resources, tutorials, or educational materials that cover percentages in more detail.
Conclusion
Calculating 65% of 200, which equals 130, is a fundamental skill with broad applicability. This article has not only provided a step-by-step guide to solving this specific problem but has also explored the broader context of percentages, highlighting their importance in various aspects of life. By understanding the underlying principles and exploring different calculation methods, you'll be well-equipped to tackle a wide array of percentage-related problems with confidence. Remember, mastering percentages is not just about getting the right answer; it's about developing a deeper understanding of this essential mathematical concept and its practical implications.
Latest Posts
Latest Posts
-
Labelled Diagram Of Reflex Arc
Sep 12, 2025
-
Wood Block And Tackle Pulley
Sep 12, 2025
-
Molar Mass Of Magnesium Phosphate
Sep 12, 2025
-
Aztec Inca And Mayan Civilizations
Sep 12, 2025
-
Are Colloids Heterogeneous Or Homogeneous
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 65 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.